Механика фрикционного контакта - Frictional contact mechanics - Wikipedia

Контактная механика это исследование деформация из твердые вещества касаются друг друга в одной или нескольких точках.^[1][2] Их можно разделить на сжимающие и адгезионные силы в направлении, перпендикулярном границе раздела, и фрикционный силы в тангенциальном направлении. Механика фрикционного контакта это исследование деформации тел при наличии фрикционных эффектов, тогда как контактная механика без трения предполагает отсутствие таких эффектов.

Механика фрикционного контакта имеет дело с большим диапазоном различных масштабов.

• В макроскопическом масштабе он применяется для исследования движения контактирующих тел (см. Контактная динамика ). Например, отскок резинового мяча о поверхность зависит от фрикционного взаимодействия на границе контакта. Здесь основное внимание уделяется суммарной силе по сравнению с вдавливанием и боковым смещением.
• В среднем масштабе интересны локальные подчеркивает, напряжения и деформации контактирующих тел в зоне контакта и рядом с ней. Например, для получения или проверки контактных моделей в макроскопическом масштабе или для исследования носить и повреждать поверхностей контактирующих тел. Области применения этой шкалы - взаимодействие шины с дорожным покрытием, взаимодействие железнодорожного колеса с рельсами, анализ подшипников качения и т. Д.
• Наконец, на микроскопических и наномасштабах контактная механика используется для улучшения нашего понимания трибологические системы (например, исследовать происхождение трение ) и для разработки передовых устройств, таких как атомно-силовые микроскопы и МЭМС устройств.

Эта страница в основном посвящена второй шкале: получению базового представления о напряжениях и деформациях в пятне контакта и рядом с ним без особого внимания к детальным механизмам, с помощью которых они возникают.

История

Несколько известных ученых, инженеров и математиков внесли свой вклад в наше понимание трения.^[3]Они включают Леонардо да Винчи, Гийом Амонтон, Иоанн Теофил Дезагулье, Леонард Эйлер, и Шарль-Огюстен де Кулон. Потом, Николай Павлович Петров, Осборн Рейнольдс и Ричард Стрибек дополнили это понимание теориями смазка.

Деформацию твердых материалов исследовали в 17-18 вв. Роберт Гук, Жозеф Луи Лагранж, а в 19-20 вв. д'Аламбер и Тимошенко. Что касается контактной механики, то классический вклад Генрих Герц^[4] выделяется. Далее фундаментальные решения Буссинеска и Черрути имеют первостепенное значение для исследования проблем контакта трения в (линейно) упругий режим.

В железнодорожных приложениях нужно знать соотношение между утечкой (разностью скоростей) ${\displaystyle \xi }$ и сила трения ${\displaystyle F_{w}}$.

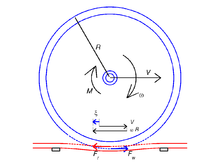
Классические результаты для задачи истинного фрикционного контакта касаются работ Ф. В. Картера (1926) и Х. Фромма (1927). Они независимо представили зависимость ползучести от силы ползучести для цилиндра на плоскости или для двух цилиндров в установившемся контакте качения, используя закон сухого трения Кулона (см. Ниже).^[5] Они применяются к тяге железнодорожных локомотивов, и для понимания охотничье колебание железнодорожного транспорта. Что касается скольжения, классические решения принадлежат К. Каттанео (1938) и Р. Д. Миндлину (1949), которые рассматривали тангенциальное смещение сферы на плоскости (см. Ниже).^[1]

В 1950-х годах интерес к контакту качения железнодорожных колес возрос. В 1958 г. Кеннет Л. Джонсон представили приближенный подход к трехмерной проблеме трения с геометрией Герца, с боковой или спиновой ползучестью. Среди прочего он обнаружил, что спиновая ползучесть, которая симметрична относительно центра пятна контакта, приводит к чистой боковой силе в условиях качения. Это связано с продольными различиями в распределении тяги в пятне контакта.

В 1967 г. Йост Жак Калкер опубликовал свою важнейшую кандидатскую диссертацию по линейной теории контакта качения.^[6] Эта теория точна для ситуации с бесконечным коэффициентом трения, когда площадь скольжения исчезает, и является приближенной для ненулевых ползучести. Он действительно принимает закон трения Кулона, который требует более или менее (тщательно) чистых поверхностей. Эта теория применима для массивных тел, таких как контакт железнодорожных колес с рельсами. Что касается взаимодействия дорожных шин, важный вклад касается так называемого волшебная формула шин к Ганс Пацейка.^[7]

В 1970-х годах было разработано множество численных моделей. Особенно вариационные подходы, например, те, кто полагается на теории существования и уникальности Дуво и Лайона. Со временем они превратились в методы конечных элементов для задач контакта с общими моделями и геометриями материалов, а также в полупространство подходы на основе так называемых контактных задач с гладкими краями для линейно-упругих материалов. Модели первой категории представил Лаурсен.^[8] и Wriggers.^[9] Примером последней категории является модель CONTACT Калкера.^[10]

Недостатком хорошо обоснованных вариационных подходов является их большое время вычисления. Поэтому было разработано много различных приближенных подходов. Несколько хорошо известных приближенных теорий для проблемы контакта качения - это подход Калкера FASTSIM, формула Шена-Хедрика-Элкинса и подход Полаха.

Более подробная информация об истории проблемы контакта колеса с рельсом представлена ​​в статье Кнота.^[5] Далее Джонсон собрал в своей книге огромное количество информации по механике контакта и связанным с ней вопросам.^[1] В отношении механики контакта качения Калкер также представляет обзор различных теорий.^[10] Наконец, представляют интерес материалы курса CISM, которые предоставляют введение в более продвинутые аспекты теории контакта качения.^[11]

Постановка проблемы

Центральным в анализе проблем с фрикционным контактом является понимание того, что подчеркивает на поверхности каждого тела пространственно различны. Следовательно, напряжения и деформации тела тоже меняются в зависимости от положения. И движение частиц контактирующих тел может быть различным в разных местах: в части пятна контакта частицы противоположных тел могут прилипать (прилипать) друг к другу, тогда как в других частях пятна контакта происходит относительное движение. Это местное относительное скольжение называется микро-соскальзывать.

Это разделение зоны контакта на зоны прилипания (сцепления) и скольжения проявляется в совокупности. в истирание. Обратите внимание, что носить происходит только там, где мощность рассеивается, что требует напряжения и местного относительного смещение (скольжение) между двумя поверхностями.

Размер и форма самого пятна контакта, а также его областей сцепления и скольжения, как правило, заранее неизвестны. Если бы они были известны, то упругие поля в двух телах можно было бы решать независимо друг от друга, и проблема больше не была бы проблемой контакта.

В контактной задаче можно выделить три различных компонента.

1. Прежде всего, это деформация отдельный тела в ответ на нагрузки, приложенные к их поверхностям. Это предмет общей механика сплошной среды. Во многом это зависит от геометрии тел и от их (учредительный ) материальное поведение (например. эластичный против. пластик отклик, однородная или слоистая структура и т. д.).
2. Во-вторых, есть общее движение тел относительно друг друга. Например, тела могут быть в покое (статика) или быстро приближаться друг к другу (влияние ), а также могут быть сдвинуты (скользящие) или повернуты (прокатка ) друг над другом. Эти общие движения обычно изучаются в классическая механика см. например многотельная динамика.
3. Наконец, есть процессы на контактном интерфейсе: сжатие и адгезия в направлении, перпендикулярном границе раздела, и трение и микро-скольжение в тангенциальные направления.

Последний аспект - первоочередная задача контактной механики. Он описывается в терминах так называемых условия контакта.Для направления, перпендикулярного границе раздела, проблема нормального контакта, эффекты адгезии обычно невелики (в больших пространственных масштабах), и обычно используются следующие условия:

1. Разрыв ${\displaystyle e_{n}}$ между двумя поверхностями должен быть нулевым (контакт) или строго положительным (разделение, ${\displaystyle e_{n}>0}$);
2. Нормальный стресс ${\displaystyle p_{n}}$ действующее на каждое тело нулевое (отрыв) или сжимающее (${\displaystyle p_{n}>0}$ на связи).

Математически: ${\displaystyle e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\!}$. Здесь ${\displaystyle e_{n},p_{n}}$ - это функции, которые меняются в зависимости от положения вдоль поверхностей тел.

В тангенциальных направлениях часто используются следующие условия:

1. Местное (касательное) напряжение сдвига ${\displaystyle {\vec {p}}=(p_{x},p_{y})^{\mathsf {T}}\,\!}$ (предполагая, что нормальное направление параллельно ${\displaystyle z}$-axis) не может превышать определенный зависящий от положения максимум, так называемый предел тяги ${\displaystyle g}$;
2. Если величина тангенциальной тяги падает ниже границы тяги ${\displaystyle \|{\vec {p}}\|<g\,\!}$, противоположные поверхности слипаются, и микропроскальзывание исчезает, ${\displaystyle {\vec {s}}=(s_{x},s_{y})^{\mathsf {T}}={\vec {0}}\,\!}$;
3. Микроскальзывание происходит там, где касательные тяги находятся на границе тяги; тогда направление тангенциальной тяги противоположно направлению микропробуксовки ${\displaystyle {\vec {p}}=-g{\vec {s}}/\|{\vec {s}}\|\,\!}$.

Точная форма границы тяги - это так называемый закон местного трения. Для этого часто локально применяется закон кулоновского (глобального) трения: ${\displaystyle \|{\vec {p}}\|\leq g=\mu p_{n}\,\!}$, с ${\displaystyle \mu }$ коэффициент трения. Также возможны более подробные формулы, например, с ${\displaystyle \mu }$ в зависимости от температуры ${\displaystyle T}$, местная скорость скольжения ${\displaystyle \|{\vec {s}}\|}$, так далее.

Решения для статических случаев

Веревка на столбике, уравнение шпиля

Иллюстрация эластичного троса, обернутого вокруг фиксированного объекта, такого как столбик. Зона контакта разделена на зоны прилипания и скольжения, в зависимости от нагрузок, действующих на обоих концах, и от истории нагружения.

Рассмотрим веревку с равными силами (например, ${\displaystyle F_{\text{hold}}=400\,\mathrm {N} }$) действуют с обеих сторон. Этим веревка немного растягивается и внутренняя напряжение ${\displaystyle T}$ индуцируется (${\displaystyle T=400\,\mathrm {N} }$ на каждой позиции вдоль веревки). Веревка наматывается на фиксированный предмет, например, столбик; он изгибается и контактирует с поверхностью объекта под углом контакта (например, ${\displaystyle 180^{\circ }}$). Между тросом и столбиком возникает нормальное давление, но трение еще не происходит. Затем усилие на одной стороне болларда увеличивается до более высокого значения (например, ${\displaystyle F_{\text{load}}=600\,\mathrm {N} }$). Это действительно вызывает напряжения сдвига при трении в зоне контакта. В конечной ситуации боллард оказывает на веревку силу трения, так что возникает статическая ситуация.

Распределение натяжения каната в этой конечной ситуации описывается уравнение кабестана, с решением:

${\displaystyle {\begin{aligned}T(\phi )&=T_{\text{hold}},&\phi &\in \left[\phi _{\text{hold}},\phi _{\text{intf}}\right]\\T(\phi )&=T_{\text{load}}e^{-\mu \phi },&\phi &\in \left[\phi _{\text{intf}},\phi _{\text{load}}\right]\\\phi _{\text{intf}}&={\frac {1}{\mu }}\log \left({\frac {T_{\text{load}}}{T_{\text{hold}}}}\right)&\end{aligned}}}$

Напряжение возрастает от ${\displaystyle T_{\text{hold}}}$ на слабой стороне (${\displaystyle \phi =\phi _{\text{hold}}}$) к ${\displaystyle T_{\text{load}}}$ на высокой стороне ${\displaystyle \phi =\phi _{\text{load}}}$. Если смотреть с высокой стороны, натяжение падает экспоненциально, пока не достигнет нижней нагрузки при ${\displaystyle \phi =\phi _{\text{intf}}}$. С этого момента это значение будет постоянным. Точка перехода ${\displaystyle \phi _{\text{intf}}}$ определяется соотношением двух нагрузок и коэффициентом трения. Здесь напряженность ${\displaystyle T}$ в Ньютонах и углах ${\displaystyle \phi }$ в радианах.

Напряженность ${\displaystyle T}$ в канате в конечном положении увеличивается по отношению к начальному состоянию. Поэтому веревка немного вытягивается. Это означает, что не все поверхностные частицы каната могли удерживать свое исходное положение на поверхности болларда. В процессе погрузки трос немного соскользнул по поверхности столбика в зона скольжения ${\displaystyle \phi \in [\phi _{\text{intf}},\phi _{\text{load}}]}$. Это скольжение достаточно велико, чтобы достичь удлинения, которое происходит в конечном состоянии. Обратите внимание, что в конечном состоянии не происходит скольжения; период, термин зона скольжения относится к проскальзыванию, которое произошло во время процесса загрузки. Обратите внимание, что расположение области скольжения зависит от начального состояния и процесса нагружения. Если начальное натяжение ${\displaystyle 600\,\mathrm {N} }$ и напряжение снижается до ${\displaystyle 400\,\mathrm {N} }$ со стороны провисания, то зона скольжения возникает на стороне провисания зоны контакта. Для начального напряжения между ${\displaystyle 400}$ и ${\displaystyle 600\,\mathrm {N} }$, на обеих сторонах могут быть участки скольжения, а между ними - липкая область.

Обобщение для веревки, лежащей на произвольной ортотропной поверхности

Если канат находится в равновесии под действием касательных сил на шероховатой ортотропной поверхности, то выполняются три следующих условия (все они):

1. Без разделения - нормальная реакция ${\displaystyle N}$ положительна для всех точек кривой веревки:

   ${\displaystyle N=-k_{n}T>0}$, куда ${\displaystyle k_{n}}$ - нормальная кривизна кривой веревки.

2. Коэффициент сопротивления трения ${\displaystyle \mu _{g}}$ и угол ${\displaystyle \alpha }$ удовлетворяют следующим критериям для всех точек кривой
   ${\displaystyle -\mu _{g}<\tan \alpha <+\mu _{g}}$
3. Предельные значения касательных сил:

   Силы на обоих концах веревки ${\displaystyle T}$ и ${\displaystyle T_{0}}$ удовлетворяют следующему неравенству

   ${\displaystyle T_{0}e^{-\int _{s}\omega \mathrm {d} s}\leq T\leq T_{0}e^{\int _{s}\omega \mathrm {d} s}}$

   с ${\displaystyle \omega =\mu _{\tau }{\sqrt {k_{n}^{2}-{\frac {k_{g}^{2}}{\mu _{g}^{2}}}}}=\mu _{\tau }k{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}$,

   куда ${\displaystyle k_{g}}$- геодезическая кривизна веревочной кривой, ${\displaystyle k}$ кривизна изгиба каната, ${\displaystyle \mu _{\tau }}$- коэффициент трения в тангенциальном направлении.

   Если ${\displaystyle \omega }$ постоянно тогда ${\displaystyle T_{0}e^{-\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}\leq T\leq T_{0}e^{\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}}$.

Это обобщение было получено Конюховым А.^[12][13]

Сфера на плоскости, (3D) проблема Каттанео

Рассмотрим сферу, которая прижимается к плоскости (полупространству), а затем перемещается по ее поверхности. Если сфера и плоскость идеализированы как твердые тела, то контакт будет происходить только в одной точке, и сфера не будет двигаться до тех пор, пока приложенная касательная сила не достигнет максимальной силы трения. Затем он начинает скользить по поверхности, пока приложенная сила снова не уменьшится.

На самом деле, с учетом упругих эффектов, дело обстоит иначе. Если упругая сфера прижимается к упругой плоскости из того же материала, то оба тела деформируются, образуется круглая контактная площадка и возникает нормальное распределение давления (Герца). Центр сферы перемещен вниз на расстояние ${\displaystyle \delta _{n}}$ называется подход, что эквивалентно максимальному проникновению недеформированных поверхностей. Для сферы радиуса ${\displaystyle R}$ и упругие постоянные ${\displaystyle E,\nu }$ это решение Герца гласит:

${\displaystyle {\begin{aligned}p_{n}(x,y)&=p_{0}{\sqrt {1-{\frac {r^{2}}{a^{2}}}}}&r&={\sqrt {x^{2}+y^{2}}}\leq a&a&={\sqrt {R\delta _{n}}}\\p_{0}&={\frac {2}{\pi }}E^{*}{\sqrt {\frac {\delta _{n}}{R}}}&F_{n}&={\frac {4}{3}}E^{*}{\sqrt {R}}\delta _{n}^{\frac {3}{2}}&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}\end{aligned}}}$

Теперь рассмотрим, что касательная сила ${\displaystyle F_{x}}$ применяется, что меньше границы кулоновского трения ${\displaystyle \mu F_{n}}$. После этого центр сферы сместится в сторону на небольшое расстояние. ${\displaystyle \delta _{x}}$ это называется сдвиг. Достигается статическое равновесие, при котором возникают упругие деформации, а также напряжения сдвига при трении на поверхности контакта. В этом случае при уменьшении тангенциальной силы уменьшаются также упругие деформации и касательные напряжения. Сфера в значительной степени возвращается в исходное положение, за исключением потерь на трение, возникающих из-за локального скольжения в пятне контакта.

Эта контактная проблема была решена Каттанео приблизительно с использованием аналитического подхода. Распределение напряжений в состоянии равновесия состоит из двух частей:

${\displaystyle {\begin{aligned}p_{x}(x,y)&=\mu p_{0}\left({\sqrt {1-{\frac {r^{2}}{a^{2}}}}}-{\frac {c}{a}}{\sqrt {1-{\frac {r^{2}}{c^{2}}}}}\right)&0\leq {}&r\leq c\\p_{x}(x,y)&=\mu p_{n}(x,y)&c\leq {}&r\leq a\\p_{x}(x,y)&=0&a\leq {}&r\end{aligned}}}$

В центральной, залипающей области ${\displaystyle 0\leq r\leq c}$, поверхностные частицы плоскости перемещаются по ${\displaystyle u_{x}=\delta _{x}/2}$ вправо, а поверхностные частицы сферы перемещаются по ${\displaystyle u_{x}=-\delta _{x}/2}$ Слева. Хотя сфера в целом движется ${\displaystyle \delta _{x}}$ относительно плоскости эти поверхностные частицы не двигались друг относительно друга. Во внешнем кольце ${\displaystyle c\leq r\leq r}$, поверхностные частицы действительно двигались относительно друг друга. Их локальный сдвиг получается как

${\displaystyle s_{x}(x,y)=\delta _{x}+u_{x}^{\text{sphere}}(x,y)-u_{x}^{\text{plane}}(x,y)}$

Этот сдвиг ${\displaystyle s_{x}(x,y)}$ настолько велика, что достигается статическое равновесие с касательными напряжениями на границе тяги в этой так называемой зоне скольжения.

Итак, при тангенциальном нагружении шара частичное скольжение происходит. Таким образом, контактная зона делится на зону скольжения, где поверхности перемещаются относительно друг друга, и зону прилипания, где они не перемещаются. В состоянии равновесия скольжение больше не происходит.

Решения для задач динамического скольжения

Решение контактной задачи состоит из состояния на границе раздела (где находится контакт, разделения области контакта на зоны прилипания и скольжения, а также нормального и касательного напряжений) плюс упругое поле внутри тел. Это решение зависит от истории контакта. Это можно увидеть в расширении проблемы Каттанео, описанной выше.

• В задаче Каттанео сфера сначала прижимается к плоскости, а затем сдвигается по касательной. Это дает частичное скольжение, как описано выше.
• Если сфера сначала сдвигается по касательной, а затем прижимается к плоскости, тогда нет разницы тангенциального смещения между противоположными поверхностями и, следовательно, нет касательного напряжения на границе контакта.
• Если приближение в нормальном направлении и тангенциальное смещение увеличиваются одновременно («косое сжатие»), то может быть достигнута ситуация с касательным напряжением, но без местного скольжения.^[2]

Это демонстрирует, что состояние в интерфейсе контакта зависит не только от относительного положения двух тел, но и от истории их движения. Другой пример этого происходит, если сфера возвращается в исходное положение. Изначально на границе контакта не было касательного напряжения. После начального сдвига произошло микропробуксовывание. Это микро-проскальзывание не полностью устраняется смещением назад. Таким образом, в конечной ситуации тангенциальные напряжения остаются на границе раздела, что выглядит как конфигурация, идентичная исходной.

Подробно влияние трения на динамические контакты (удары) рассмотрено в. ^[14]

Решение проблем с контактом качения

Контакт качения между цилиндром и плоскостью. Частицы, движущиеся через область контакта справа налево, напрягаются все больше и больше, пока не наступит локальное скольжение.

Задачи с подвижным контактом - это динамические задачи, в которых контактирующие тела непрерывно перемещаются относительно друг друга.Отличие от задач с динамическим скользящим контактом состоит в большем разнообразии состояний различных поверхностных частиц. В то время как пятно контакта в задаче скольжения постоянно состоит из более или менее одних и тех же частиц, в случае проблемы контакта качения частицы постоянно входят в пятно контакта и покидают его. Более того, в задаче о скольжении все поверхностные частицы в пятне контакта подвергаются более или менее одинаковому тангенциальному сдвигу повсюду, тогда как в задаче качения поверхностные частицы подвергаются весьма различным нагрузкам. Они не испытывают напряжения при входе в пятно контакта, затем прилипают к частице противоположной поверхности, деформируются из-за общей разницы в движении между двумя телами, пока не будет превышен локальный предел тяги и не наступит локальное скольжение. разные этапы для разных участков контактной площадки.

Если общее движение тел постоянно, то может быть достигнуто общее устойчивое состояние. Здесь состояние каждой поверхностной частицы меняется во времени, но общее распределение может быть постоянным. Это формализуется с помощью системы координат, которая движется вместе с пятном контакта.

Катание цилиндра по плоскости, (2D) решение Картера-Фромма

Рассмотрим цилиндр, который катится по плоскости (полупространству) в установившихся условиях с не зависящей от времени продольной утечкой ${\displaystyle \xi }$. (Относительно) далеко от концов цилиндров ситуация плоская деформация возникает, и проблема является двумерной.

Если цилиндр и плоскость состоят из одних и тех же материалов, то на проблему нормального контакта не влияет напряжение сдвига. Контактная площадка - полоска ${\displaystyle x\in [-a,a]}$, а давление описывается (2D) решением Герца.

${\displaystyle {\begin{aligned}p_{n}(x)&={\frac {p_{0}}{a}}{\sqrt {a^{2}-x^{2}}}&|x|&\leq a&a^{2}&={\frac {4F_{n}R}{\pi E^{*}}}\\p_{0}&={\frac {2F_{n}}{\pi a}}&&&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}&\end{aligned}}}$

Распределение напряжения сдвига описывается решением Картера-Фромма. Он состоит из области сцепления на передней кромке области контакта и области скольжения на задней кромке. Длина зоны сцепления обозначается ${\displaystyle 2a'}$. Далее координата адгезии вводится как ${\displaystyle x'=x+a-a'}$. В случае положительной силы ${\displaystyle F_{x}>0}$ (отрицательная ползучесть ${\displaystyle \xi <0}$) это:

${\displaystyle {\begin{aligned}p_{x}(x)&=0&|&x|\geq a\\p_{x}(x)&={\frac {\mu p_{0}}{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a-2a'\leq {}&x\leq a\\p_{x}(x)&=\mu p_{n}(x)&&x\leq a-2a'\end{aligned}}}$

Размер области сцепления зависит от утечки, радиуса колеса и коэффициента трения.

${\displaystyle {\begin{aligned}a'&=a{\sqrt {1-{\frac {|F_{x}|}{\mu F_{n}}}}},&{\mbox{for }}|F_{x}|\leq \mu F_{n}\\\xi &=-\operatorname {sign} (F_{x})\,{\frac {\mu (a-a')}{R}},&{\mbox{i.e. }}|\xi |\leq {\frac {\mu a}{R}}\\F_{x}&=-\operatorname {sign} (\xi )\,\mu F_{n}\left(1-\left(1+{\frac {R|\xi |}{\mu a}}\right)^{2}\right)\end{aligned}}}$

Для больших ползучести ${\displaystyle a'=0}$ так что происходит полное скольжение.

Подходы на основе полупространства

При рассмотрении контактных задач на промежуточных пространственных масштабах мелкомасштабные неоднородности материала и шероховатость поверхности не учитываются. Считается, что тела состоят из гладких поверхностей и однородных материалов. Применяется континуальный подход, при котором напряжения, деформации и перемещения описываются (кусочно) непрерывными функциями.

В полупространство Подход представляет собой элегантную стратегию решения так называемых "гладких" или "концентрированных" контактных задач.

1. Если массивное упругое тело нагружено на небольшом участке его поверхности, то упругие напряжения затухают пропорционально ${\displaystyle 1/distance^{2}}$ а упругие смещения на ${\displaystyle 1/distance}$ когда человек удаляется от этой поверхности.
2. Если тело не имеет острых углов в зоне контакта или рядом с ней, то его реакция на поверхностную нагрузку может быть хорошо аппроксимирована реакцией упругого полупространства (например, всех точек ${\displaystyle (x,y,z)^{\mathsf {T}}\in \mathbb {R} ^{3}\,\!}$ с ${\displaystyle z>0\,\!}$).
3. Задача упругого полупространства решена аналитически, см. Решение Буссинеска-Черрути.
4. Из-за линейности этого подхода можно наложить несколько частных решений.

Используя фундаментальное решение для полупространства, полная трехмерная контактная задача сводится к двумерной задаче для ограничивающих поверхностей тел.

Дальнейшее упрощение происходит, если два тела «геометрически и упруго подобны». В общем, напряжение внутри тела в одном направлении вызывает смещения и в перпендикулярных направлениях. Следовательно, существует взаимодействие между нормальным напряжением и касательными смещениями в контактной задаче, а также взаимодействие между касательным напряжением и нормальными смещениями. Но если нормальное напряжение на границе контакта вызывает одинаковые тангенциальные смещения в обоих контактирующих телах, то относительного тангенциального смещения двух поверхностей не происходит. В этом случае проблемы нормального и касательного контакта разделены. В этом случае два тела называются квазиидентичный. Это происходит, например, если тела зеркально-симметричны относительно плоскости контакта и имеют одинаковые упругие постоянные.

Классические решения, основанные на подходе полупространства:

1. Герц решил контактную задачу в отсутствие трения для простой геометрии (криволинейные поверхности с постоянным радиусом кривизны).
2. Картер рассмотрел контакт качения между цилиндром и плоскостью, как описано выше. Для тангенциальной тяги предоставляется полное аналитическое решение.
3. Каттанео рассмотрел сжатие и смещение двух сфер, как описано выше. Обратите внимание, что это аналитическое решение является приблизительным. На самом деле небольшие тангенциальные тяги ${\displaystyle p_{y}}$ происходят, которые игнорируются.

Смотрите также

• Адгезионная железная дорога - Железная дорога, которая использует сцепную тягу для движения поезда
• Несущий - Механизм ограничения относительного движения до желаемого движения и уменьшения трения
• Контактная механика - Исследование деформации соприкасающихся друг с другом твердых тел
• (Линейная) эластичность - Физическое свойство, когда материалы или объекты возвращаются к исходной форме после деформации
• Энергетически модифицированный цемент - Класс цемента, механически обработанный для преобразования реакционной способности
• Трение - Сила, препятствующая относительному движению твердых поверхностей, слоев жидкости и элементов материала, скользящих друг относительно друга.
• Привод трения - Механическая передача мощности за счет трения между компонентами
• Смазка - Наличие материала для уменьшения трения между двумя поверхностями.
• Металлургия - Область материаловедения, изучающая физическое и химическое поведение металлов.
• Многотельная система - инструмент для изучения динамического поведения связанных между собой твердых или гибких тел;
• Пластичность - Деформация твердого материала, претерпевающая необратимые изменения формы под действием приложенных сил.
• Прокат (металлообработка) - Процесс обработки металла
• Механика твердого тела - Раздел механики, связанный с твердыми материалами и их поведением
• Тороидальный или роликовый вариатор (Extroid CVT) - Автоматическая коробка передач, которая может плавно переключаться в непрерывном диапазоне эффективных передаточных чисел
• Трибология - Наука и техника взаимодействующих поверхностей в относительном движении
• Динамика автомобиля
• Носить - Повреждение, постепенное удаление или деформация материала на твердых поверхностях

Рекомендации

1. Джонсон, К. (1985). Контактная механика. Кембридж: Издательство Кембриджского университета.
2. Попов, В. (2010). Контактная механика и трение. Физические принципы и приложения. Берлин: Springer-Verlag.
3. «Введение в трибологию - трение». Получено 2008-12-21.
4. Герц, Генрих (1882 г.). «Контакт между твердыми упругими телами». Journal für die Reine und Angewandte Mathematik. 92.
5. Knothe, К. (2008). «История механики контакта колеса с рельсами: от Редтенбахера до Калкера». Динамика системы автомобиля. 46 (1–2): 9–26. Дои:10.1080/00423110701586469.
6. Калкер, Джуст Дж. (1967). О контакте качения двух упругих тел при наличии сухого трения. Делфтский технологический университет.
7. Пацейка, Ганс (2002). Шины и динамика автомобиля. Оксфорд: Баттерворт-Хайнеманн.
8. Лаурсен, Т.А., 2002, Вычислительная механика контакта и удара, основы моделирования межфазных явлений в нелинейном конечно-элементном анализе, Springer, Берлин
9. Риггерс, П., 2006, Вычислительная механика контакта, 2-е изд., Springer, Гейдельберг
10. Калкер, Дж. Дж. (1990). Трехмерные упругие тела в контакте качения. Дордрехт: Kluwer Academic Publishers.
11. Б. Якобсен и Дж. Дж. Калкер, изд. (2000). Явления подвижного контакта. Вена, Нью-Йорк: Springer-Verlag.
12. Конюхов, Александр (01.04.2015). «Контакт канатов с ортотропными шероховатыми поверхностями». Журнал прикладной математики и механики. 95 (4): 406–423. Bibcode:2015ЗаММ ... 95..406К. Дои:10.1002 / zamm.201300129. ISSN  1521-4001.
13. Конюхов А., Изи Р. «Введение в вычислительную механику контакта: геометрический подход». Вайли.
14. Виллерт, Эмануэль (2020). Stoßprobleme in Physik, Technik und Medizin: Grundlagen und Anwendungen (на немецком). Springer Vieweg.

внешняя ссылка

• [1]^{[постоянная мертвая ссылка ]} Биография профессора д.р. J.J. Калкер (Делфтский технологический университет).
• [2] Программное обеспечение Kalker Hertzian / non-Hertzian CONTACT.