Квадратная черепица сота - Square tiling honeycomb

Смотрите также: Квадратная черепица Заказать-4 соты

Квадратная черепица сота
Тип	Гиперболические обычные соты Паракомпактные однородные соты
Символы Шлефли	{4,4,3} г {4,4,4} {4^1,1,1}
Диаграммы Кокстера	↔ ↔ ↔
Клетки	{4,4}
Лица	квадрат {4}
Край фигура	треугольник {3}
Фигура вершины	куб, {4,3}
Двойной	Орден-4 соты восьмигранные
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {N}}_{3}}$, [4^3] ${\displaystyle {\overline {M}}_{3}}$, [4^1,1,1]
Характеристики	Обычный

в геометрия из гиперболическое 3-пространство, то квадратная черепица соты является одним из 11 паракомпактных обычных сот. Это называется паракомпакт потому что он бесконечен клетки, вершины которого существуют на ориосферы и сходятся к единому идеальная точка на бесконечности. Дано Символ Шлефли {4,4,3}, у него три квадратные мозаики, {4,4} вокруг каждого ребра и шесть квадратных мозаик вокруг каждой вершины в кубический {4,3} вершина фигуры.^[1]

А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.

Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.

Ректифицированная квадратная черепица порядка 4

Он также выглядит как выпрямленная квадратная мозаичная сотовая структура порядка 4, r {4,4,4}:

{4,4,4}	г {4,4,4} = {4,4,3}
	=

Симметрия

Соты квадратной черепицы имеют три конструкции отражающей симметрии: как обычные соты, полусимметричная конструкция ↔ , и, наконец, конструкция с тремя типами (цветами) клетчатых квадратных мозаик ↔ .

Он также содержит подгруппу индекса 6 [4,4,3^*] ↔ [4^1,1,1] и радиальная подгруппа [4, (4,3)^*] индекса 48, с правом двугранный восьмигранный фундаментальная область, и четыре пары ультрапараллельных зеркал: .

Эти соты содержат эта плитка 2-гиперцикл поверхности, похожие на паракомпактные апейрогональная мозаика порядка 3 :

Связанные многогранники и соты

Соты с квадратной черепицей - это обычные гиперболические соты в 3-м пространстве. Это один из одиннадцати обычных паракомпактных сот.

11 паракомпактных обычных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

Есть пятнадцать однородных сот в [4,4,3] Группа Коксетера семья, включая эту регулярную форму, и ее двойной, то октаэдрические соты порядка 4, {3,4,4}.

[4,4,3] семейные соты

{4,4,3}	г {4,4,3}	т {4,4,3}	рр {4,4,3}	т0,3{4,4,3}	tr {4,4,3}	т0,1,3{4,4,3}	т0,1,2,3{4,4,3}
{3,4,4}	г {3,4,4}	т {3,4,4}	rr {3,4,4}	2т {3,4,4}	tr {3,4,4}	т0,1,3{3,4,4}	т0,1,2,3{3,4,4}

Соты квадратной черепицы являются частью квадратная черепица порядка 4 сот семейство, как это можно видеть как выпрямленные соты квадратной черепицы порядка 4.

[4,4,4] семейные соты
{4,4,4}	г {4,4,4}	т {4,4,4}	rr {4,4,4}	т0,3{4,4,4}	2т {4,4,4}	tr {4,4,4}	т0,1,3{4,4,4}	т0,1,2,3{4,4,4}

Это связано с 24-элементный, {3,4,3}, который также имеет кубическую вершину. Он также является частью последовательности сот с квадратная черепица клетки:

{4,4, п} соты v т е
Космос	E^3	ЧАС^3
Форма	Аффинный	Паракомпакт		Некомпактный
Имя	{4,4,2}	{4,4,3}	{4,4,4}	{4,4,5}	{4,4,6}	...{4,4,∞}
Coxeter
Изображение
Вершина фигура	{4,2}	{4,3}	{4,4}	{4,5}	{4,6}	{4,∞}

Выпрямленный квадратный сотовый заполнитель

Выпрямленный квадратный сотовый заполнитель
Тип	Паракомпактные однородные соты Полуправильные соты
Символы Шлефли	r {4,4,3} или t1{4,4,3} 2r {3,4^1,1} г {4^1,1,1}
Диаграммы Кокстера	↔ ↔ ↔
Клетки	{4,3} г {4,4}
Лица	квадрат {4}
Фигура вершины	треугольная призма
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {O}}_{3}}$, [3,4^1,1] ${\displaystyle {\overline {M}}_{3}}$, [4^1,1,1]
Характеристики	Вершинно-транзитивный, реберный транзитивный

В ректифицированная квадратная черепичная сотовая структура, т₁{4,4,3}, имеет куб и квадратная черепица грани, с треугольная призма вершина фигуры.

Он похож на двумерную гиперболическую форму триапейрогональная мозаика, r {∞, 3}, причем треугольник и апейрогональный лица.

Усеченный квадратный черепичный сотовый

Усеченный квадратный черепичный сотовый
Тип	Паракомпактные однородные соты
Символы Шлефли	т {4,4,3} или т0,1{4,4,3}
Диаграммы Кокстера	↔ ↔
Клетки	{4,3} т {4,4}
Лица	квадрат {4} восьмиугольник {8}
Фигура вершины	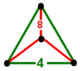треугольная пирамида
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {N}}_{3}}$, [4^3] ${\displaystyle {\overline {M}}_{3}}$, [4^1,1,1]
Характеристики	Вершинно-транзитивный

В усеченный квадратный черепичный сотовый, т {4,4,3}, имеет куб и усеченная квадратная мозаика грани, с треугольная пирамида вершина фигуры. Это то же самое, что и усеченный квадратный квадратный сотовый заполнитель порядка 4, tr {4,4,4}, .

Сотовый квадрат с усеченной плиткой

Сотовый квадрат с усеченной плиткой
Тип	Паракомпактные однородные соты
Символы Шлефли	2т {4,4,3} или т1,2{4,4,3}
Диаграмма Кокстера
Клетки	т {4,3} т {4,4}
Лица	треугольник {3} квадрат {4} восьмиугольник {8}
Фигура вершины	дигональный дисфеноид
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В усеченный квадратный мозаичный сотовый, 2t {4,4,3}, имеет усеченный куб и усеченная квадратная мозаика грани, с дигональный дисфеноид вершина фигуры.

Квадратный квадратный черепичный сотовый

Квадратный квадратный черепичный сотовый
Тип	Паракомпактные однородные соты
Символы Шлефли	rr {4,4,3} или t0,2{4,4,3}
Диаграммы Кокстера	↔
Клетки	г {4,3} рр {4,4} {} x {3}
Лица	треугольник {3} квадрат {4}
Фигура вершины	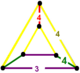равнобедренный треугольная призма
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В скошенные квадратные черепичные соты, rr {4,4,3}, имеет кубооктаэдр, квадратная черепица, и треугольная призма фасеточный, с равнобедренным треугольная призма вершина фигуры.

Сота с усеченной квадратной черепицей

Сота с усеченной квадратной черепицей
Тип	Паракомпактные однородные соты
Символы Шлефли	tr {4,4,3} или t0,1,2{4,4,3}
Диаграмма Кокстера
Клетки	т {4,3} tr {4,4} {} x {3}
Лица	треугольник {3} квадрат {4} восьмиугольник {8}
Фигура вершины	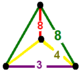равнобедренный треугольная пирамида
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В усеченный квадратный черепичный сотовый, tr {4,4,3}, имеет усеченный куб, усеченная квадратная мозаика, и треугольная призма фасеточный, с равнобедренным треугольная пирамида вершина фигуры.

Ячеистые соты с квадратной черепицей

Ячеистые соты с квадратной черепицей
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,3{4,4,3}
Диаграммы Кокстера	↔
Клетки	{3,4} {4,4} {} x {4} {} x {3}
Лица	треугольник {3} квадрат {4}
Фигура вершины	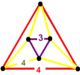нерегулярный треугольная антипризма
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В сотовый заполненный квадратной черепицей, т_0,3{4,4,3}, имеет октаэдр, треугольная призма, куб, и квадратная черепица грани, с неправильной треугольная антипризма вершина фигуры.

Сота с усеченной квадратной черепицей

Сота с усеченной квадратной черепицей
Тип	Паракомпактные однородные соты
Символы Шлефли	т0,1,3{4,4,3} s2,3{3,4,4}
Диаграммы Кокстера
Клетки	рр {4,3} т {4,4} {} x {3} {} x {8}
Лица	треугольник {3} квадрат {4} восьмиугольник {8}
Фигура вершины	равнобедренно-трапециевидный пирамида
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В усеченный квадратный черепичный сотовый, т_0,1,3{4,4,3}, имеет ромбокубооктаэдр, восьмиугольная призма, треугольная призма и усеченная квадратная мозаика граней, с равнобедренно-трапециевидный пирамида вершина фигуры.

Ячеистые соты с квадратными гранями

В соты с квадратной черепицей такой же, как восьмигранные соты усеченного порядка-4.

Сота с укороченной квадратной черепицей

Сота с укороченной квадратной черепицей
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,1,2,3{4,4,3}
Диаграмма Кокстера
Клетки	tr {4,4} {} x {6} {} x {8} tr {4,3}
Лица	квадрат {4} шестиугольник {6} восьмиугольник {8}
Фигура вершины	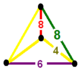нерегулярный тетраэдр
Группы Кокстера	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Характеристики	Вершинно-транзитивный

В усеченный квадратный мозаичный сотовый, т_0,1,2,3{4,4,3}, имеет усеченная квадратная мозаика, усеченный кубооктаэдр, шестиугольная призма, и восьмиугольная призма грани, с неправильной тетраэдр вершина фигуры.

Омниснуб квадратная черепица сотовая

Омниснуб квадратная черепица сотовая
Тип	Паракомпактные однородные соты
Символ Шлефли	ч (т0,1,2,3{4,4,3})
Диаграмма Кокстера
Клетки	sr {4,4} ср {2,3} sr {2,4} sr {4,3}
Лица	треугольник {3} квадрат {4}
Фигура вершины	нерегулярный тетраэдр
Группа Коксетера	[4,4,3]^+
Характеристики	Неравномерный, вершинно-транзитивный

В чередующиеся соты с укороченной квадратной черепицей (или же omnisnub квадратная черепица сотовая), h (t_0,1,2,3{4,4,3}), имеет плоская квадратная черепица, курносый куб, треугольная антипризма, квадратная антипризма, и тетраэдр ячейки, с нерегулярным тетраэдр вершина фигуры.

Сота с чередованием квадратных плиток

Сота с чередованием квадратных плиток
Тип	Паракомпактные однородные соты Полуправильные соты
Символ Шлефли	ч {4,4,3} ч. {4,4,4} {(4,3,3,4)} ч {4^1,1,1}
Диаграммы Кокстера	↔ ↔ ↔ ↔ ↔ ↔
Клетки	{4,4} {4,3}
Лица	квадрат {4}
Фигура вершины	кубооктаэдр
Группы Кокстера	${\displaystyle {\overline {O}}_{3}}$, [3,4^1,1] [4,1^+,4,4] ↔ [∞,4,4,∞] ${\displaystyle {\widehat {BR}}_{3}}$, [(4,4,3,3)] [1^+,4^1,1,1] ↔ [∞^[6]]
Характеристики	Вершинно-транзитивный, реберный транзитивный, квазирегулярный

В чередующиеся квадратные сотовые ячейки, ч {4,4,3}, это квазирегулярный паракомпактные однородные соты в гиперболическом 3-м пространстве. Она имеет куб и квадратная черепица грани в кубооктаэдр фигура вершины.

Сотовая черепица кантик-квадрат

Сотовая черепица кантик-квадрат
Тип	Паракомпактные однородные соты
Символ Шлефли	час2{4,4,3}
Диаграммы Кокстера	↔
Клетки	т {4,4} г {4,3} т {4,3}
Лица	треугольник {3} квадрат {4} восьмиугольник {8}
Фигура вершины	прямоугольный пирамида
Группы Кокстера	${\displaystyle {\overline {O}}_{3}}$, [3,4^1,1]
Характеристики	Вершинно-транзитивный

В кантик квадратная черепица сотовая, ч₂{4,4,3}, представляет собой паракомпактные однородные соты в трехмерном гиперболическом пространстве. Она имеет усеченная квадратная мозаика, усеченный куб, и кубооктаэдр грани, с прямоугольный пирамида вершина фигуры.

Сотовая черепица Runcic Square

Сотовидная черепица Runcic Square
Тип	Паракомпактные однородные соты
Символ Шлефли	час3{4,4,3}
Диаграммы Кокстера	↔
Клетки	{4,4} г {4,3} {3,4}
Лица	треугольник {3} квадрат {4}
Фигура вершины	квадрат усеченный
Группы Кокстера	${\displaystyle {\overline {O}}_{3}}$, [3,4^1,1]
Характеристики	Вершинно-транзитивный

В Ранчо квадратная черепица сотовая, ч₃{4,4,3}, представляет собой паракомпактные однородные соты в трехмерном гиперболическом пространстве. Она имеет квадратная черепица, ромбокубооктаэдр, и октаэдр грани в квадрат усеченный фигура вершины.

Сотовая черепица Runcantic Square

Сотовая черепица Runcicantic Square
Тип	Паракомпактные однородные соты
Символ Шлефли	час2,3{4,4,3}
Диаграммы Кокстера	↔
Клетки	т {4,4} tr {4,3} т {3,4}
Лица	квадрат {4} шестиугольник {6} восьмиугольник {8}
Фигура вершины	зеркальная клиновидная кость
Группы Кокстера	${\displaystyle {\overline {O}}_{3}}$, [3,4^1,1]
Характеристики	Вершинно-транзитивный

В Сотовая черепица Runcantic Square, ч_2,3{4,4,3}, ↔ , представляет собой паракомпактные однородные соты в трехмерном гиперболическом пространстве. Она имеет усеченная квадратная мозаика, усеченный кубооктаэдр, и усеченный октаэдр грани в зеркальная клиновидная кость вершина фигуры.

Чередующиеся ректифицированные сотовые ячейки квадратной черепицы

Чередующиеся ректифицированные сотовые ячейки квадратной черепицы
Тип	Паракомпактные однородные соты
Символ Шлефли	ч. {4,4,3}
Диаграммы Кокстера	↔
Клетки
Лица
Фигура вершины	треугольная призма
Группы Кокстера	[4,1^+,4,3] = [∞,3,3,∞]
Характеристики	Несимплектический, вершинно-транзитивный

В чередующиеся ректифицированные сотовые ячейки квадратной черепицы представляет собой паракомпактные однородные соты в трехмерном гиперболическом пространстве.

Смотрите также

• Выпуклые однородные соты в гиперболическом пространстве
• Регулярные мозаики гиперболического 3-мерного пространства
• Паракомпактные однородные соты

Рекомендации

1. Coxeter Красота геометрии, 1999, Глава 10, Таблица III

• Coxeter, Правильные многогранники, 3-й. изд., Dover Publications, 1973. ISBN  0-486-61480-8. (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
• Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN  99-35678, ISBN  0-486-40919-8 (Глава 10, Регулярные соты в гиперболическом пространстве ) Таблица III
• Джеффри Р. Уикс Форма космоса, 2-е издание ISBN  0-8247-0709-5 (Глава 16-17: Геометрии на трехмерных многообразиях I, II)
• Норман Джонсон Равномерные многогранники, Рукопись
  • N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
  • N.W. Джонсон: Геометрии и преобразования, (2018) Глава 13: Гиперболические группы Кокстера
  • Норман У. Джонсон и Азия Ивич Вайс Квадратичные целые числа и группы Кокстера PDF Может. J. Math. Vol. 51 (6), 1999, стр. 1307–1336