Карта аргументов - Argument map

Схематическая карта аргументов, показывающая утверждение (или вывод), поддерживающие аргументы и возражения, а также возражение вывода.
Деталь Древа познания по энциклопедии Дидро и Даламбера, автор Кретьен Фредерик Гийом Рот
Отображение информации
Темы и поля
Подходы между узлами
Смотрите также

В неформальная логика и философия, карта аргументов или же диаграмма аргументов это наглядное представление структуры аргумент. Карта аргументов обычно включает ключевые компоненты аргумента, традиционно называемые вывод и предпосылки, также называемый раздор и причины.[1] Карты аргументов также могут отображать совместные помещения, возражения, контраргументы, опровержения, и леммы. Существуют разные стили отображения аргументов, но они часто функционально эквивалентны и представляют отдельные утверждения аргумента и отношения между ними.

Карты аргументов обычно используются в контексте обучения и применения критическое мышление.[2] Цель составления карты - выявить логическую структуру аргументов, выявить неустановленные предположения, оценить поддержку, которую аргумент предлагает для вывода, и помочь в понимании дебатов. Карты аргументов часто предназначены для поддержки обсуждения вопросов, идей и аргументов в злые проблемы.[3]

Карту аргументов не следует путать с Диаграмма связей или карта разума, два других вида диаграмма узел – звено которые имеют разные ограничения на узлы и ссылки.[4]

Ключевая особенность

Было предложено несколько различных видов карт аргументов, но самый распространенный, который Крис Рид и Гленн Роу назвали стандартная диаграмма,[5] состоит из древовидная структура с каждой из причин, ведущих к заключению. Нет единого мнения относительно того, должно ли заключение быть наверху дерева вместе с причинами, ведущими к нему, или должно быть внизу с причинами, ведущими к нему.[5] В другом варианте аргумент изображен слева направо.[6]

В соответствии с Дуглас Н. Уолтон и его коллег, карта аргументов состоит из двух основных компонентов: «Один компонент - это набор чисел в кружках, расположенных в виде точек. Каждое число представляет предложение (посылку или вывод) в схематическом аргументе. Другой компонент представляет собой набор линий или стрелок. соединение точек. Каждая линия (стрелка) представляет собой вывод. Вся сеть точек и линий представляет собой своего рода обзор рассуждений в данном аргументе ... "[7] С появлением программного обеспечения для создания карт аргументов стало обычным явлением, что карты аргументов состоят из блоков, содержащих фактические предложения, а не чисел, ссылающихся на эти утверждения.

Существуют разногласия по поводу терминологии, которая будет использоваться при описании карт аргументов,[8] но стандартная диаграмма содержит следующие структуры:

Зависимые помещения или же совместные помещения, где хотя бы одно из соединенных посылок требует другой посылки, прежде чем оно сможет поддержать вывод: аргумент с такой структурой был назван связаны аргумент.[9]

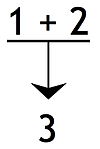
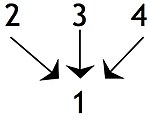
Пункты 1 и 2 - это зависимые помещения или совместные помещения

Независимые помещения, где посылка может поддерживать вывод сама по себе: хотя независимые посылки могут в совокупности сделать вывод более убедительным, это следует отличать от ситуаций, когда посылка не поддерживает заключение, если она не соединена с другой посылкой. Если несколько посылок или групп посылок приводят к окончательному выводу, аргумент может быть описан как сходящийся. Это отличается от расходящийся аргумент, когда одна посылка может использоваться для подтверждения двух отдельных выводов.[10]

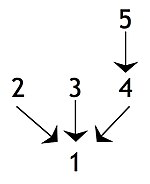
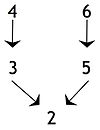
Утверждения 2, 3, 4 - самостоятельные помещения.

Промежуточные выводы или же подвыводы, когда утверждение подтверждается другим утверждением, которое, в свою очередь, используется для подтверждения некоторого дополнительного утверждения, то есть окончательного вывода или другого промежуточного вывода: на следующей диаграмме утверждение 4 является промежуточным выводом в том смысле, что это вывод по отношению к утверждению 5 но является предпосылкой по отношению к окончательному выводу, т.е. утверждению 1. Аргумент с такой структурой иногда называют сложный аргумент. Если существует единственная цепочка утверждений, содержащая хотя бы один промежуточный вывод, аргумент иногда описывается как серийный аргумент или цепь аргумент.[11]

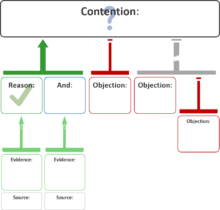
Утверждение 4 является промежуточным выводом или подвыводом.

Каждая из этих структур может быть представлена ​​эквивалентным подходом «прямоугольник и линия» к картам аргументов. На следующей диаграмме раздор отображается вверху, а связанные с ним прямоугольники представляют причины, которые включают один или несколько предпосылки. Зеленая стрелка указывает на то, что два причины поддержать раздор:

Коробка и линейная диаграмма

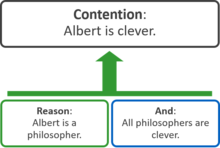
Карты аргументов также могут представлять контраргументы. На следующей диаграмме два возражения ослабить раздор, в то время как причины поддержать предпосылка возражения:

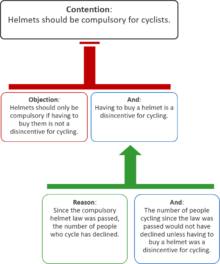
Пример аргумента с использованием возражений

Представление аргумента в виде карты аргументов

Составление схем письменного текста

Письменный текст можно преобразовать в карту аргументов, выполнив последовательность шагов. Монро Бердсли книга 1950 года Практическая логика рекомендуется следующая процедура:[12]

  1. Выражения разделяйте скобками и нумеруйте их.
  2. Обведите кружками логические индикаторы.
  3. В скобках укажите любые опущенные логические индикаторы.
  4. Изложите утверждения на диаграмме, на которой стрелки показывают отношения между утверждениями.
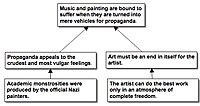
Схема примера от Бердсли Практическая логика

Бердсли привел первый пример такого анализа текста:

Хотя ① [люди, которые говорят о "социальной значимости" искусства, не хотят этого признавать], ② [музыка и живопись неизбежно пострадают, когда их превратят в простые средства пропаганды]. За ③ [пропаганда апеллирует к самым грубым и пошлым чувствам]: (за) ④ [посмотрите на академические чудовища, созданные официальными нацистскими художниками]. Что важнее, ⑤ [искусство должно быть самоцелью для художника], потому что ⑥ [художник может делать лучшие работы только в атмосфере полной свободы].

Бердсли сказал, что вывод в этом примере - утверждение. Утверждение ④ необходимо переписать как декларативное предложение, например «Академические чудовища [были] созданы официальными нацистскими художниками». Утверждение ① указывает на то, что заключение не всеми принимается, но утверждение ① опущено на диаграмме, потому что оно не поддерживает вывод. Бердсли сказал, что логическая связь между утверждением ③ и утверждением ④ неясна, но он предложил диаграмму утверждения в качестве вспомогательного утверждения ③.

Прямоугольная и линейная диаграмма примера Бердсли, построенная с использованием процедуры Харрелла.

Совсем недавно профессор философии Марали Харрелл рекомендовала следующую процедуру:[13]

  1. Определите все претензии автора.
  2. Перепишите их как независимые утверждения, исключив несущественные слова.
  3. Определите, какие утверждения являются предпосылками, промежуточными выводами и основным выводом.
  4. Дайте недостающие, подразумеваемые выводы и подразумеваемые предпосылки. (Это необязательно в зависимости от цели карты аргументов.)
  5. Поместите утверждения в ячейки и проведите линию между всеми связанными ячейками.
  6. Обозначьте поддержку от предпосылки (я) к (под) заключению стрелками.

Диаграмма как мышление

Карты аргументов полезны не только для представления и анализа существующих писаний, но и для обдумывания проблем как части процесс структурирования проблемы или же процесс написания.[14] Использование такого анализа аргументов для обдумывания проблем получило название «рефлексивной аргументации».[15]

Карта аргументов, в отличие от Древо решений, не говорит о том, как принять решение, но о процессе выбора последовательный должность (или отражающее равновесие ) на основе структуры карты аргументов можно представить в виде дерева решений.[16]

История

Философские истоки и традиция картирования аргументов

Из «Элементов логики Уэйтли», с. 467, издание 1852 г.

в Элементы логики, который был опубликован в 1826 году и выпущен во многих последующих изданиях,[17] Архиепископ Ричард Уэйтли представил, вероятно, первую форму карты аргументов, представив ее с предположением, что «многие студенты, вероятно, найдут очень ясный и удобный способ демонстрации логического анализа хода аргументации, чтобы нарисовать его в форме Дерева. , или логическое деление ".

Однако этот метод не получил широкого распространения, возможно, потому, что для сложных аргументов он требовал большого количества переписывания и переписывания предпосылок.

Таблица улик Вигмора, 1905 г.

Философ и теоретик права Джон Генри Вигмор подготовил карты юридических аргументов с использованием пронумерованных помещений в начале 20 века,[18] частично основанный на идеях философа 19 века Генри Сиджвик кто использовал линии для обозначения отношений между терминами.[19]

Диаграммы аргументов англоязычных людей в 20 веке

Как справиться с неудачей формальный сокращение неформальной аргументации, англоговорящий теория аргументации разработал схематические подходы к неформальному рассуждению в течение пятидесяти лет.

Монро Бердсли предложил форму диаграммы аргументов в 1950 году.[12] Его метод разметки аргумента и представления его компонентов связанными числами стал стандартом и до сих пор широко используется. Он также ввел терминологию, которая все еще актуальна для описания сходящийся, расходящийся и серийный аргументы.

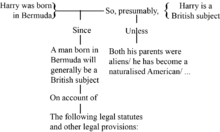
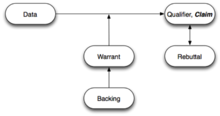
А Диаграмма аргументов Тулмина, перерисованный с его 1959 г. Использование аргумента
Обобщенная диаграмма Тулмина

Стивен Тулмин в своей новаторской и влиятельной книге 1958 года Использование аргументов,[20] определили несколько элементов аргумента, которые были обобщены. В Диаграмма Тулмина широко используется в педагогическом критическом обучении.[21][22] Хотя Тулмин в конечном итоге оказал значительное влияние на развитие неформальная логика он оказал небольшое первоначальное влияние, и подход Бердсли к построению диаграмм аргументов вместе с его более поздними разработками стал стандартным подходом в этой области. Тулмин представил кое-что, чего не хватало в подходе Бердсли. В Бердсли "стрелки связывают причины и выводы (но) не подтверждается сама импликация между ними. Не существует теории, другими словами, вывода, отличного от логического вывода, отрывок всегда считается не спорным и не подлежащим обсуждению. поддержка и оценка ».[23] Тулмин представил концепцию ордер который «можно рассматривать как представление причин, лежащих в основе вывода, поддержки, которая разрешает ссылку».[24]

Подход Бердсли был усовершенствован Стивеном Н. Томасом, чья книга 1973 г. Практическое мышление на естественном языке[25] ввел термин связаны описать аргументы, в которых предпосылки обязательно работали вместе, чтобы поддержать вывод.[26] Однако фактическое различие между зависимыми и независимыми помещениями проводилось до этого.[26] Введение связанной структуры позволило картам аргументов представлять отсутствующие или «скрытые» предпосылки. Кроме того, Томас предложил указать причины как за и против заключение с причинами против представлены пунктирными стрелками. Томас ввел термин диаграмма аргументов и определил основные причины как те, которые не были поддержаны другими в аргументе и окончательный вывод как то, что не использовалось для подтверждения какого-либо дальнейшего вывода.

Диаграмма аргументов Скривена. Явная посылка 1 соединяется с дополнительными невысказанными посылками a и b, чтобы влечь 2.

Майкл Скривен далее развил подход Бердсли-Томаса в своей книге 1976 г. Рассуждение.[27] Принимая во внимание, что Бердсли сказал: «Сначала запишите утверждения ... после небольшой практики обращайтесь к утверждениям только по номерам».[28] Скривен выступал за разъяснение значения утверждений, перечисление их, а затем использование древовидной диаграммы с числами для отображения структуры. Недостающие предпосылки (невысказанные предположения) должны были быть включены и обозначены буквой алфавита вместо числа, чтобы выделить их из явных утверждений. Скривен представил контраргументы в своих диаграммах, которые Тулмин определил как опровержение.[29] Это также позволило составить диаграмму аргументов «сбалансированности».[30]

В 1998 г. компания выпустила серию крупномасштабных карт аргументов. Роберт Э. Хорн стимулировал широкий интерес к отображению аргументов.[31]

Разработка компьютерной визуализации аргументов

Взаимодействие человека с компьютером пионер Дуглас Энгельбарт в известном техническом отчете 1962 г. увеличение интеллекта, подробно рассматривал что-то вроде программного обеспечения для сопоставления аргументов как неотъемлемую часть будущих компьютерных интерфейсов, повышающих интеллект:[32]

Вы обычно думаете об аргументе как о последовательной последовательности шагов разума, начинающейся с известных фактов, предположений и т. Д. И продвигающейся к выводу. Что ж, нам действительно нужно продумывать эти шаги последовательно, и мы обычно перечисляем шаги последовательно, когда записываем их, потому что это в значительной степени способ их представления в наших статьях и книгах - они довольно ограничивают символическую структуру, которую они позволяют нам использовать. ... Чтобы помочь нам лучше понять структуру аргумента, мы также можем вызвать схематическое или графическое отображение. После того, как будут установлены связи между предшествующим и последующим, компьютер может автоматически построить для нас такое отображение.

— Дуглас Энгельбарт, «Расширение человеческого интеллекта: концептуальные рамки» (1962).

В середине-конце 1980-х гг. гипертекст программные приложения которые поддерживали визуализацию аргументов, в том числе Карты для заметок и гибис; последний сгенерировал на экране графическую гипертекстовую карту проблемно-информационная система, модель аргументации, разработанная Вернером Кунцем и Хорст Риттель в 1970-е гг.[33] В 1990-е годы Тим ван Гелдер и его коллеги разработали серию программных приложений, которые позволили полностью указать и отредактировать исходные данные карты аргументов на диаграмме, а не в легенде.[34] Первую программу Ван Гелдера, Reason! Able, заменили две последующие программы, bCisive и Rationale.[35]

На протяжении 1990-х и 2000-х годов было разработано множество других программных приложений для визуализации аргументов. К 2013 году существовало более 60 таких программных комплексов.[36] В обзоре компьютерной аргументации в 2010 году Оливер Шойер и его коллеги отметили, что одно из различий между этими программными системами заключается в том, поддерживается ли совместная работа.[37] В их обзоре однопользовательские системы аргументации включали Convince Me, iLogos, LARGO, Athena, Араукария, и Карнеад; системы аргументации малых групп включали Digalo, QuestMap, Компендиум, Бельведер и AcademicTalk; системы аргументации сообщества включены Дебатеграф и Коллаборатория.[37]

Приложения

Карты аргументов применялись во многих областях, но прежде всего в образовательных, академических и деловых условиях, включая обоснование дизайна.[38] Карты аргументов также используются в Криминалистика,[39] закон, и искусственный интеллект.[40] Также было высказано предположение, что отображение аргументов имеет большой потенциал для улучшения нашего понимания и реализации демократии, в связи с продолжающейся эволюцией электронная демократия.[41]

Трудности с философской традицией

Традиционно было трудно отделить обучение критическому мышлению от философской традиции преподавания. логика и методики, и большинство учебников критического мышления были написаны философами. Неформальная логика учебники изобилуют философскими примерами, но неясно, переносится ли подход в таких учебниках на студентов, не изучающих философию.[21] Похоже, что после таких занятий статистический эффект незначителен. Однако, согласно многим исследованиям, отображение аргументов дает измеримый эффект.[42] Например, было показано, что обучение картированию аргументов улучшает навыки критического мышления студентов, изучающих бизнес.[43]

Доказательства того, что отображение аргументов улучшает способность критического мышления

Существуют эмпирические доказательства того, что навыки, приобретенные на курсах критического мышления, основанного на картировании аргументов, существенно переходят в критическое мышление без картирования аргументов. Мета-анализ Альвареса показал, что такие курсы критического мышления дали прирост около 0,70. SD, примерно вдвое больше, чем стандартные курсы критического мышления.[44] В рассмотренных исследованиях использовались стандартные тесты на критическое мышление.

Как отображение аргументов помогает при критическом мышлении

Использование сопоставления аргументов произошло в ряде дисциплин, таких как философия, управленческая отчетность, военный и разведывательный анализ, а также публичные дебаты.[38]

  • Логическая структура: Карты аргументов отображают логическую структуру аргумента более четко, чем стандартный линейный способ представления аргументов.
  • Концепции критического мышления: Изучая карту аргументов, студенты усваивают такие ключевые понятия критического мышления, как «причина», «возражение», «предпосылка», «заключение», «вывод», «опровержение», «неустановленное предположение», «совместная предпосылка», «сила доказательства», «логическая структура», «независимое доказательство» и т. д. Овладение такими понятиями - это не просто вопрос запоминания их определений или даже умения правильно их применять; это также понимание того, почему различия, отмечаемые этими словами, важны, и использование этого понимания для направления своих рассуждений.
  • Визуализация: Люди очень наглядны, и отображение аргументов может предоставить студентам базовый набор визуальных схем, с помощью которых можно понять структуры аргументов.
  • Более внимательно читать и слушать: Изучение карты аргументов учит людей читать и слушать более внимательно и выдвигает на первый план ключевые вопросы «Какова логическая структура этого аргумента?» и «Как это предложение вписывается в общую структуру?» Таким образом, более вероятна углубленная когнитивная обработка.
  • Более осторожное письмо и говорение: Сопоставление аргументов помогает людям более точно излагать свои рассуждения и доказательства, потому что рассуждения и доказательства должны явно вписываться в логическую структуру карты.
  • Буквальное и предполагаемое значение: Часто многие утверждения в аргументе не подтверждают в точности то, что имел в виду автор. Изучение карты аргументов улучшает сложный навык отличать буквальное значение от предполагаемого.
  • Экстернализация: Запись чего-либо и анализ написанного часто помогает выявить пробелы и прояснить свои мысли. Поскольку логическая структура карт аргументов более ясна, чем у линейной прозы, преимущества сопоставления будут превосходить преимущества обычного письма.
  • Ожидание ответов: Для критического мышления важно предвидеть возражения и учитывать правдоподобность различных опровержений. Составление карт развивает этот навык ожидания и, таким образом, улучшает анализ.

Стандарты

Формат обмена аргументами

Основная статья: Формат обмена аргументами

Формат обмена аргументами (AIF) - это международная попытка разработать репрезентативный механизм для обмена ресурсами аргументов между исследовательскими группами, инструментами и областями с использованием семантически богатого языка.[45] AIF-RDF - это расширенная онтология, представленная в Структура описания ресурсов Семантический язык схемы (RDFS). Хотя АиФ по-прежнему остается подвижной целью, он успокаивается.[46]

Формат обмена юридическими знаниями

Основная статья: Формат обмена юридическими знаниями

Формат обмена юридическими знаниями (LKIF)[47] разработан в европейском проекте ESTRELLA[48] и разработан с целью стать стандартом для представления и обмена политиками, законодательством и делами, включая их оправдательные аргументы, в правовой сфере. LKIF основывается и использует Язык веб-онтологий (OWL) для представления концепций и включает многоразовую базовую онтологию юридических концепций.

Argdown

Argdown - это Markdown -вдохновленный облегченный язык разметки для сложной аргументации.[49] Он предназначен для обмена аргументами и их реконструкций в общедоступном и высоко человек читаемый путь. Синтаксис Argdown сопровождается инструментами, которые упрощают кодирование и преобразовывают документы Argdown в карты аргументов.[50]

Смотрите также

Примечания

  1. ^ Фримен 1991, стр. 49–90
  2. ^ Например: Дэвис 2012; Facione 2016, п. 88–112; Фишер 2004; Келли 2014, п. 73; Кунш, Шнарр и ван Тайл 2014; Уолтон 2013, п. 10; ван Гельдер 2015
  3. ^ Например: Калмзее и Авати, 2013 г.; Хоффманн и Боренштейн 2013; Меткалф и Састровардойо 2013; Рики Ол, «Компьютерная визуализация аргументов: моделирование в консультативной демократии вокруг злых проблем», в Окада, Букингем Шам и Шерборн 2014, стр. 361–380
  4. ^ Например: Дэвис 2010; Охотник 2008; Окада, Букингем Шам и Шерборн 2014, стр. vii – x, 4
  5. ^ а б Рид и Роу 2007, п. 64
  6. ^ Например: Уолтон 2013, стр. 18–20
  7. ^ Рид, Уолтон и Маканьо 2007, п. 2
  8. ^ Фримен 1991, стр. 49–90; Рид и Роу 2007
  9. ^ Харрелл 2010, п. 19
  10. ^ Фриман 1991, стр. 91–110; Харрелл 2010, п. 20
  11. ^ Бердсли 1950, стр. 18–19; Рид, Уолтон и Маканьо 2007, стр. 3–8; Харрелл 2010, стр. 19–21
  12. ^ а б Бердсли 1950
  13. ^ Харрелл 2010, п. 28
  14. ^ Это связано с различием между «сообщением знаний» и «преобразованием знаний» в исследования композиции: см., например, Chryssafidou 2014, стр. 38–39, 413
  15. ^ Например: Хоффманн и Боренштейн 2013; Хоффманн 2016; Хоффманн 2018
  16. ^ См. Раздел 4.2, «Карты аргументов как инструменты рассуждения» в Брун и Бец 2016
  17. ^ Вайтли 1834 (впервые опубликовано в 1826 г.)
  18. ^ Вигмор 1913
  19. ^ Гудвин 2000
  20. ^ Тулмин 2003 (впервые опубликовано в 1958 г.)
  21. ^ а б Саймон, Эрдуран и Осборн, 2006 г.
  22. ^ Böttcher & Meisert 2011; Маканьо и Константиниду 2013
  23. ^ Рид, Уолтон и Маканьо 2007, п. 8
  24. ^ Рид, Уолтон и Маканьо 2007, п. 9
  25. ^ Томас 1997 (впервые опубликовано в 1973 г.)
  26. ^ а б Снок Хенкеманс 2000, п. 453
  27. ^ Scriven 1976
  28. ^ Бердсли 1950, п. 21 год
  29. ^ Рид, Уолтон и Маканьо 2007, стр. 10–11
  30. ^ van Eemeren et al. 1996 г., п. 175
  31. ^ Холмс 1999; Рог 1998; Роберт Э. Хорн, «Инфраструктура для навигации по междисциплинарным дебатам: важные решения для представления аргументации», в Киршнер, Букингем Шам и Карр 2003, стр. 165–184
  32. ^ Энгельбарт 1962; Отчет о месте Энгельбарта в истории компьютерной визуализации аргументов см., Например, в Simon Buckingham Shum, «Корни компьютерной визуализации аргументов», в Киршнер, Букингем Шам и Карр 2003, стр. 3–24
  33. ^ Конклин и Бегеман 1988, на гибис; Халаш 1988, на Карты для заметок; Киршнер, Букингем Шам и Карр 2003, pp. 14–15, о месте обоих в истории компьютерной визуализации аргументов.
  34. ^ ван Гельдер 2007
  35. ^ Berg et al. 2009 г.
  36. ^ Уолтон 2013, п. 11
  37. ^ а б Scheuer et al. 2010 г.
  38. ^ а б Киршнер, Букингем Шам и Карр 2003; Окада, Букингем Шам и Шерборн 2014
  39. ^ Например: Bex 2011
  40. ^ Например: Верхей 2005; Рид, Уолтон и Маканьо 2007; Уолтон 2013
  41. ^ Гильберт 2009
  42. ^ Тварди 2004; Альварес Ортис 2007; Харрелл 2008; Янна Райдер и Нил Томасон, «Познавательные и педагогические преимущества сопоставления аргументов: LAMP направляет путь к лучшему мышлению», в Окада, Букингем Шам и Шерборн 2014, стр. 113–134; Дуайер 2011; Дэвис 2012
  43. ^ Carrington et al. 2011 г.; Кунш, Шнарр и ван Тайл 2014
  44. ^ Альварес Ортис 2007, стр. 69–70 и далее
  45. ^ Увидеть Оригинальное описание проекта AIF (2006) и полные спецификации онтологии AIF-RDF в RDFS формат.
  46. ^ Bex et al. 2013
  47. ^ Бур, Винкельс и Витали, 2008 г.
  48. ^ «Сайт проекта Estrella». estrellaproject.org. Архивировано из оригинал на 2016-02-12. Получено 2016-02-24.
  49. ^ Видеть Фойгт 2014. Веб-сайт Argdown argdown.org. Argdown в настоящее время разрабатывается как проект с открытым исходным кодом: "christianvoigt / argdown: простой синтаксис для сложной аргументации". GitHub.com. Получено 2019-10-30.
  50. ^ Инструменты Argdown включают веб-браузер песочница редактор, расширение за Код Visual Studio, а командная строка инструмент; видеть "Начиная". argdown.org. Получено 2019-10-30.

Рекомендации

дальнейшее чтение