Триангулированная категория - Triangulated category
В математика, а триангулированная категория это категория с дополнительной структурой «функтора трансляции» и класса «точных треугольников». Яркими примерами являются производная категория из абелева категория, так же хорошо как стабильная гомотопическая категория. Точные треугольники обобщают короткие точные последовательности в абелевой категории, а также последовательности волокон и последовательности кофайбер в топологии.
Много гомологическая алгебра разъясняется и расширяется языком триангулированных категорий, важным примером является теория когомологии пучков. В 1960-е годы типичным использованием триангулированных категорий было расширение свойств пучков на пространство. Икс комплексам пучков, рассматриваемых как объекты производной категории пучков на Икс. В последнее время триангулированные категории сами по себе стали объектами интереса. Было доказано или предположено множество эквивалентностей между триангулированными категориями разного происхождения. Например, гомологическая зеркальная симметрия гипотеза предсказывает, что производная категория Многообразие Калаби – Яу эквивалентен Категория Фукая своего "зеркала" симплектическое многообразие.
История
Триангулированные категории были введены независимо Дитером Пуппе (1962) и Жан-Луи Вердье (1963), хотя аксиомы Пуппе были менее полными (без октаэдрической аксиомы (TR 4)).[1] Puppe был мотивирован категорией стабильной гомотопии. Ключевым примером Вердье была производная категория абелевой категории, которую он также определил, развивая идеи Александр Гротендик. Ранние приложения производных категорий включали когерентная двойственность и Двойственность Вердье, который расширяет Двойственность Пуанкаре в особые пространства.
Определение
А сдвиг или же функтор перевода по категории D аддитивный автоморфизм (или, по мнению некоторых авторов, авто-эквивалентность ) из D к D. Обычно пишут для целых чисел п.
А треугольник (Икс, Y, Z, ты, v, ш) состоит из трех объектов Икс, Y, и Zвместе с морфизмами , и . Треугольники обычно пишут в развернутом виде:
или же
для краткости.
А триангулированная категория является аддитивная категория D с функтором трансляции и классом треугольников, называемым точные треугольники[2] (или же выдающиеся треугольники), удовлетворяющие следующим свойствам (TR 1), (TR 2), (TR 3) и (TR 4). (Эти аксиомы не являются полностью независимыми, поскольку (TR 3) может быть получено из других.[3])
TR 1
- Для каждого объекта Икс, следующий треугольник является точным:
- Для любого морфизма , есть объект Z (называется конус или же кофеварка морфизма ты) вписывается в точный треугольник
- Название «конус» происходит от конус карты цепные комплексы, который, в свою очередь, был вдохновлен картографический конус в топологии. Из других аксиом следует, что точный треугольник (и в частности объект Z) определяется с точностью до изоморфизма морфизмом , хотя и не всегда с точностью до единственного изоморфизма.[4]
- Каждый треугольник, изоморфный точному треугольнику, точен. Это означает, что если
- - точный треугольник, и , , и являются изоморфизмами, то
- также является точным треугольником.
TR 2
Если
является точным треугольником, то два повернутых треугольника тоже
и
С учетом последнего треугольника объект Z[−1] называется волокно морфизма .
Второй повернутый треугольник имеет более сложную форму, когда и не являются изоморфизмами, а являются только взаимно обратными эквивалентностями категорий, поскольку это морфизм из к , и получить морфизм к нужно сочинять с естественным преобразованием . Это приводит к сложным вопросам о возможных аксиомах, которые необходимо наложить на естественные преобразования, и в пару обратных эквивалентностей. В связи с этой проблемой предположение, что и взаимно обратные изоморфизмы - обычный выбор в определении триангулированной категории.
TR 3
Учитывая два точных треугольника и отображение между первыми морфизмами в каждом треугольнике, существует морфизм между третьими объектами в каждом из двух треугольников, который делает все ездят. То есть на следующей диаграмме (где две строки представляют собой точные треугольники и ж и грамм морфизмы такие, что гу = уф) существует отображение час (не обязательно уникальный), заставляя все квадраты коммутировать:
TR 4: Октаэдрическая аксиома
Позволять и быть морфизмами, и рассмотрим составной морфизм . Сформируйте точные треугольники для каждого из этих трех морфизмов согласно TR 1. Аксиома октаэдра утверждает (примерно), что три конуса отображения могут быть превращены в вершины точного треугольника так, чтобы «все коммутировало».
Более формально, учитывая точные треугольники
- ,
существует точный треугольник
такой, что
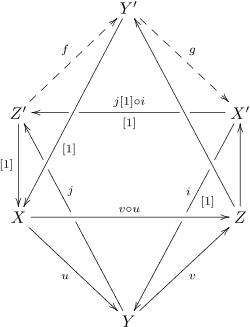
Эта аксиома называется «октаэдрической аксиомой», потому что рисование всех объектов и морфизмов дает скелет октаэдр, четыре грани которых представляют собой точные треугольники. Представленная здесь презентация принадлежит Вердье и появляется вместе с октаэдрической диаграммой в (Hartshorne1966 ). На следующей диаграмме ты и v - данные морфизмы, а буквы со штрихом - конусы различных отображений (выбраны так, чтобы каждый точный треугольник имел Икс, а Y, а Z письмо). Различные стрелки помечены [1], чтобы указать, что они имеют «степень 1»; например карта из Z' к Икс на самом деле из Z' к Икс[1]. Тогда аксиома октаэдра утверждает существование отображений ж и грамм образуя точный треугольник, и чтобы ж и грамм образуют коммутативные треугольники на других гранях, которые их содержат:
Две разные картинки появляются в (Beilinson, Bernstein & Deligne1982 ) (Гельфанд и Манин (2006 ) также представляю первую). Первый представляет верхнюю и нижнюю пирамиды вышеуказанного октаэдра и утверждает, что, учитывая нижнюю пирамиду, можно заполнить верхнюю пирамиду так, чтобы два пути от Y к Y', и из Y' к Y, равны (это условие опущено, возможно, по ошибке, в презентации Хартшорна). Треугольники, помеченные знаком +, коммутативны, а треугольники с меткой d точны:
Вторая диаграмма представляет собой более инновационное представление. Точные треугольники представлены линейно, и диаграмма подчеркивает тот факт, что четыре треугольника в «октаэдре» соединены серией отображений треугольников, где три треугольника (а именно, те, которые завершают морфизмы из Икс к Y, из Y к Z, и из Икс к Z) даны и утверждается существование четвертого. Один проходит между первыми двумя, "вращаясь" вокруг Икс, к третьему, поворачиваясь вокруг Z, а к четвертому, поворачиваясь вокруг Икс′. Все вложения на этой диаграмме коммутативны (как тригоны, так и квадрат), но другой коммутативный квадрат, выражающий равенство двух путей из Y' к Y, не очевидно. Все стрелки, указывающие «за край», имеют степень 1:
Эта последняя диаграмма также иллюстрирует полезную интуитивную интерпретацию аксиомы октаэдра. В триангулированных категориях треугольники играют роль точных последовательностей, и поэтому наводит на размышления об этих объектах как о «частных», и . Таким образом, существование последнего треугольника выражает, с одной стороны,
- (глядя на треугольник ), и
- (глядя на треугольник ).
Собирая их вместе, аксиома октаэдра утверждает «третью теорему об изоморфизме»:
Если триангулированная категория является производной категорией D(А) абелевой категории А, и Икс, Y, Z являются объектами А рассматриваются как комплексы, сосредоточенные в степени 0, а карты и являются мономорфизмами в А, то конусы этих морфизмов в D(А) фактически изоморфны приведенным выше частным в А.
Наконец, Нееман (2001 ) формулирует аксиому октаэдра, используя двумерную коммутативную диаграмму с 4 строками и 4 столбцами. Бейлинсон, Бернштейн и Делинь (1982 ) также дают обобщения аксиомы октаэдра.
Характеристики
Вот несколько простых следствий аксиом для триангулированной категории D.
- Учитывая точный треугольник
- в D, композиция любых двух последовательных морфизмов равна нулю. То есть, ву = 0, wv = 0, ты[1]ш = 0 и так далее.[5]
- Учитывая морфизм , TR 1 гарантирует существование конуса Z завершение точного треугольника. Любые два конуса ты изоморфны, но изоморфизм не всегда определяется однозначно.[4]
- Каждый мономорфизм в D есть включение прямого слагаемого, , и каждый эпиморфизм это проекция .[6] С этим связано то, что не следует говорить об «инъективности» или «сюръективности» для морфизмов в триангулированной категории. Каждый морфизм не является изоморфизмом, имеет ненулевое "коядро" Z (это означает, что существует точный треугольник ), а также ненулевое «ядро», а именно Z[−1].
Нефункциональность конструкции конуса
Одна из технических сложностей с триангулированными категориями заключается в том, что конструкция конуса не является функториальной. Например, учитывая кольцо и частичное отображение выделенных треугольников
в , есть две карты, которые завершают эту диаграмму. Это может быть карта идентичности или нулевая карта
оба коммутативны. Тот факт, что существует две карты, является тенью того факта, что триангулированная категория - это инструмент, который кодирует гомотопические пределы и копредел. Одно решение этой проблемы было предложено Гротендик где рассматривается не только производная категория, но и производная категория диаграмм этой категории. Такой объект называется Дериватор.
Примеры
- Векторные пространства через поле k образуют элементарную триангулированную категорию, в которой Икс[1] = Икс для всех Икс. Точный треугольник - это последовательность из k-линейные карты (написание той же карты дважды), который точный в Икс, Y и Z.
- Если А аддитивная категория (например, абелева категория), определим гомотопическая категория иметь объекты комплексы в А, а как морфизмы гомотопические классы морфизмов комплексов. потом - триангулированная категория.[7] Смена Икс[1] - это комплекс Икс перемещен на один шаг влево (и с дифференциалами, умноженными на -1). Точный треугольник в - треугольник, изоморфный в к треугольнику связанный с какой-то картой цепных комплексов. (Здесь обозначает картографический конус карты цепи.)
- В производная категория D(А) абелевой категории А - триангулированная категория.[8] Построен из категории комплексов. C(А) к локализация по отношению ко всем квазиизоморфизмы. То есть формально присоединить обратный морфизм к каждому квазиизоморфизму. Объекты D(А) без изменений; то есть они представляют собой цепные комплексы. Точный треугольник в D(А) - треугольник, изоморфный в D(А) к треугольнику связанный с какой-то картой цепных комплексов.
Ключевым мотивом для производной категории является то, что производные функторы на А можно рассматривать как функторы производной категории.[9] Некоторые естественные подкатегории D(А) также являются триангулированными категориями, например подкатегория комплексов Икс чьи объекты когомологии в А исчезнуть для я достаточно отрицательный, достаточно положительный или и то и другое, называемые , соответственно. - В топологии стабильная гомотопическая категория - триангулированная категория.[10] Объекты спектры, смена Икс[1] - это приостановка (или, что то же самое, разворот ), а точные треугольники - это последовательности волокон. Отличительная черта стабильной гомотопической категории (по сравнению с нестабильная гомотопическая категория ) состоит в том, что последовательности волокон такие же, как последовательности волокон. Фактически, в любой триангулированной категории точные треугольники можно рассматривать как последовательности волокон, а также как последовательности волокон.
- В модульная теория представлений конечной группы грамм, то категория стабильного модуля StMod (кг) - триангулированная категория. Его объекты - это представления грамм над полем k, а морфизмы - обычные по модулю морфизмов, разлагаемых на множители проективный (или эквивалентно инъективный ) кг-модули. В более общем смысле, категория стабильных модулей определяется для любого Алгебра Фробениуса на месте кг.
Есть ли лучшие аксиомы?
Некоторые эксперты подозревают[11]стр.190 (см., например, (Гельфанд, Манин2006, Введение, Глава IV)), что триангулированные категории не совсем "правильное" понятие. Существенная причина в том, что конус морфизма единственен только с точностью до неуникальный изоморфизм. В частности, конус морфизма, вообще говоря, не зависит от функционально на морфизме (отметим, например, неединственность в аксиоме (TR 3)). Эта неуникальность - потенциальный источник ошибок. Однако аксиомы адекватно работают на практике, и их изучению посвящено множество литературы.
Дериваторы
Одно из альтернативных предложений - теория производные предложенный Гротендиком в книге «Преследование стеков» в 80-х гг.[11]стр. 191, а позже развил в 90-х годах в своей рукописи по этой теме. По сути, это система гомотопических категорий, задаваемых категориями диаграмм для категории с классом слабых эквивалентностей . Эти категории затем связаны морфизмами диаграмм . Этот формализм имеет то преимущество, что он может восстановить пределы гомотопии и копределы, что заменяет конструкцию конуса.
Стабильные ∞-категории
Другая построенная альтернатива - это теория стабильные ∞-категории. Гомотопическая категория стабильной ∞-категории канонически триангулируется, и, кроме того, конусы отображения становятся по существу уникальными (в точном гомотопическом смысле). Более того, стабильная ∞-категория естественным образом кодирует целую иерархию совместимости для своей гомотопической категории, в основании которой находится аксиома октаэдра. Таким образом, дать данные стабильной ∞-категории строго сильнее, чем предоставить данные триангуляции ее гомотопической категории. Почти все триангулированные категории, которые возникают на практике, происходят из стабильных ∞-категорий. Аналогичным (но более специальным) обогащением триангулированных категорий является понятие dg-категория.
В некотором смысле стабильные ∞-категории или dg-категории работают лучше, чем триангулированные категории. Одним из примеров является понятие точного функтора между триангулированными категориями, обсуждаемое ниже. Для гладкий проективное разнообразие Икс над полем k, ограниченная производная категория когерентные пучки происходит из dg-категории естественным образом. Для сортов Икс и Y, каждый функтор из dg-категории Икс к тому из Y происходит из комплекса связок на посредством Преобразование Фурье – Мукаи.[12] Напротив, есть пример точного функтора из к что не происходит из комплекса связок на .[13] В свете этого примера «правильное» понятие морфизма между триангулированными категориями, кажется, происходит из морфизма лежащих в основе dg-категорий (или стабильных ∞-категорий).
Еще одно преимущество стабильных ∞-категорий или dg-категорий перед триангулированными категориями проявляется в алгебраическая K-теория. Можно определить алгебраическую K-теорию стабильной ∞-категории или dg-категории C, задающую последовательность абелевых групп для целых чисел я. Группа имеет простое описание в терминах триангулированной категории, связанной с C. Но пример показывает, что высшие K-группы dg-категории не всегда определяются связанной триангулированной категорией.[14] Таким образом, триангулированная категория имеет четко определенную группа, но в целом не высшие K-группы.
С другой стороны, теория триангулированных категорий проще, чем теория стабильных ∞-категорий или dg-категорий, и во многих приложениях достаточно триангулированной структуры. Пример - доказательство Гипотеза Блоха – Като, где многие вычисления производились на уровне триангулированных категорий, и дополнительная структура ∞-категорий или dg-категорий не требовалась.
Когомологии в триангулированных категориях
Триангулированные категории допускают понятие когомологий, и каждая триангулированная категория имеет большой запас когомологических функторов. А когомологический функтор F из триангулированной категории D к абелевой категории А - функтор такой, что для каждого точного треугольника
последовательность в А точно. Поскольку точный треугольник определяет бесконечную последовательность точных треугольников в обоих направлениях,
когомологический функтор F на самом деле дает длинная точная последовательность в абелевой категории А:
Ключевой пример: для каждого объекта B в триангулированной категории D, функторы и когомологичны, со значениями в категории абелевы группы.[15] (Чтобы быть точным, последний контравариантный функтор, который можно рассматривать как функтор на противоположная категория из D.) То есть точный треугольник определяет две длинные точные последовательности абелевых групп:
и
Для определенных триангулированных категорий эти точные последовательности дают многие важные точные последовательности в когомологиях пучков, групповые когомологии, и другие области математики.
Можно также использовать обозначение
для целых чисел я, обобщая Функтор Ext в абелевой категории. В этих обозначениях первая точная последовательность выше будет записана:
Для абелевой категории А, еще один базовый пример когомологического функтора на производной категории D(А) посылает сложный Икс к объекту в А. То есть точный треугольник в D(А) определяет длинную точную последовательность в А:
используя это .
Точные функторы и эквивалентности
An точный функтор (также называемый триангулированный функтор) из триангулированной категории D в триангулированную категорию E является аддитивным функтором который, грубо говоря, коммутирует с трансляцией и переводит точные треугольники в точные треугольники.[16]
Более подробно, точный функтор имеет естественный изоморфизм (где первый обозначает функтор трансляции D а второй обозначает функтор трансляции E), что всякий раз, когда
это точный треугольник в D,
это точный треугольник в E.
An эквивалентность триангулированных категорий является точным функтором это тоже эквивалентность категорий. В этом случае существует точный функтор такой, что FG и GF естественно изоморфны соответствующим тождественным функторам.
Компактно сгенерированные триангулированные категории
Позволять D - триангулированная категория такая, что прямые суммы индексированные произвольным набором (не обязательно конечным) существуют в D. Объект Икс в D называется компактный если функтор ездит с прямыми суммами. В явном виде это означает, что для каждого семейства объектов в D проиндексировано набором S, естественный гомоморфизм абелевых групп является изоморфизмом. Это отличается от общего понятия компактный объект в теории категорий, которая включает в себя все копределы, а не только копроизведения.
Например, компактный объект в стабильной гомотопической категории - конечный спектр.[17] Компактный объект в производной категории кольца или в квазикогерентный производная категория схемы, является идеальный комплекс. В случае гладкого проективного многообразия Икс над полем категория Perf (Икс) совершенных комплексов также можно рассматривать как ограниченную производную категорию когерентных пучков, .
Триангулированная категория D является компактно генерируемый если
- D имеет произвольные (не обязательно конечные) прямые суммы;
- Есть набор S компактных объектов в D так что для каждого ненулевого объекта Икс в D, есть объект Y в S с ненулевым отображением для некоторого целого числа п.
Многие естественные "большие" триангулированные категории генерируются компактно:
- Производная категория модулей над кольцом р компактно порождается одним объектом, р-модуль р.
- Квазикогерентная производная категория квазикомпактный квазиразделенная схема компактно порождается одним объектом.[18]
- Стабильная гомотопическая категория компактно порождается одним объектом - сферным спектром .[19]
Амнон Ниман обобщил Теорема Брауна о представимости в любую компактно порожденную триангулированную категорию следующим образом.[20] Позволять D - компактно порожденная триангулированная категория, когомологический функтор, переводящий копроизведения в продукты. потом ЧАС представимо. (То есть есть объект W из D такой, что для всех Икс.) Для другой версии пусть D - компактно порожденная триангулированная категория, Т любая триангулированная категория. Если точный функтор отправляет сопродукты к сопродуктам, затем F имеет правый смежный.
Теорема Брауна о представимости может использоваться для определения различных функторов между триангулированными категориями. В частности, Ниман использовал его для упрощения и обобщения конструкции исключительный функтор обратного изображения для морфизма ж из схемы, центральная особенность когерентная двойственность теория.[21]
т-структуры
Для каждой абелевой категории А, производная категория D(А) - триангулированная категория, содержащая А как полная подкатегория (комплексы, сосредоточенные в нулевой степени). Различные абелевы категории могут иметь эквивалентные производные категории, так что не всегда возможно восстановить А из D(А) как триангулированная категория.
Александр Бейлинсон, Джозеф Бернштейн и Пьер Делинь описал эту ситуацию понятием т-структура по триангулированной категории D.[22] Т-структура на D определяет абелеву категорию внутри D, и различные t-структуры на D может давать разные абелевы категории.
Локализация и толстые подкатегории
Позволять D - триангулированная категория с произвольными прямыми суммами. А локализация подкатегории из D это строго полный триангулированная подкатегория, замкнутая относительно произвольных прямых сумм.[23] Чтобы объяснить название: если подкатегория локализации S компактно порожденной триангулированной категории D генерируется набором объектов, то есть Локализация Боусфилда функтор с ядром S.[24] (То есть для каждого объекта Икс в D есть точный треугольник с Y в S и LX в право ортогональный .) Например, эта конструкция включает локализация спектра при простом числе, или ограничение комплекса пучков на пространстве на открытое подмножество.
Для «малых» триангулированных категорий больше подходит параллельное понятие: толстая подкатегория триангулированной категории C - строго полная триангулированная подкатегория, замкнутая относительно прямых слагаемых. (Если C является идемпотентно-полный подкатегория толстая тогда и только тогда, когда она также идемпотентно-полная.) Локализующая подкатегория толстая.[25] Так что если S является локализующей подкатегорией триангулированной категории D, то пересечение S с подкатегорией компактных объектов - толстая подкатегория .
Например, Девинац–Хопкинс –Смит описал все толстые подкатегории триангулированной категории конечных спектров в терминах Моравская К-теория.[26] Локализующие подкатегории всей стабильной гомотопической категории не классифицированы.
Смотрите также
- Преобразование Фурье – Мукаи
- Шесть операций
- Извращенная связка
- D-модуль
- Локализация Бейлинсона – Бернштейна
- Спектр модуля
- Полуортогональное разложение
- Условие устойчивости Бриджеланда
Примечания
- ^ Пуппе (1962, 1967); Вердье (1963, 1967).
- ^ Weibel (1994), определение 10.2.1.
- ^ Дж. Питер Мэй, Аксиомы для триангулированных категорий.
- ^ а б Weibel (1994), замечание 10.2.2.
- ^ Weibel (1994), упражнение 10.2.1.
- ^ Гельфанд и Манин (2006), Упражнение IV.1.1.
- ^ Кашивара и Шапира (2006), теорема 11.2.6.
- ^ Вейбель (1994), следствие 10.4.3.
- ^ Weibel (1994), раздел 10.5.
- ^ Вейбель (1994), теорема 10.9.18.
- ^ а б Гротендик. "Погоня за стеками". thescrivener.github.io. В архиве (PDF) из оригинала на 30 июл 2020. Получено 2020-09-17.
- ^ Тоен (2007), теорема 8.15.
- ^ Риццардо и др. (2019), теорема 1.4.
- ^ Даггер и Шипли (2009), замечание 4.9.
- ^ Weibel (1994), пример 10.2.8.
- ^ Вейбель (1994), определение 10.2.6.
- ^ Neeman (2001), замечание D.1.5.
- ^ Stacks Project, Тег 09IS, Stacks Project, Тег 09М1.
- ^ Neeman (2001), лемма D.1.3.
- ^ Neeman (1996), теоремы 3.1 и 4.1.
- ^ Neeman (1996), пример 4.2.
- ^ Бейлинсон и др. (1982), Определение 1.3.1.
- ^ Neeman (2001), Введение, после замечания 1.4.
- ^ Краузе (2010), теорема, введение.
- ^ Neeman (2001), замечание 3.2.7.
- ^ Равенель (1992), теорема 3.4.3.
Рекомендации
Вот некоторые вводные в учебниках триангулированные категории:
- Гельфанд, Сергей; Манин Юрий (2006), «IV. Триангулированные категории», Методы гомологической алгебры, Монографии Springer по математике (2-е изд.), Springer-Verlag, Дои:10.1007/978-3-662-12492-5, ISBN 978-3540435839, МИСТЕР 1950475
- Кашивара, Масаки; Шапира, Пьер (2006), Категории и связки, Grundlehren der Mathematischen Wissenschaften, Берлин, Нью-Йорк: Springer-Verlag, Дои:10.1007/3-540-27950-4, ISBN 978-3-540-27949-5, МИСТЕР 2182076
- Вейбель, Чарльз А. (1994). Введение в гомологическую алгебру. Кембриджские исследования в области высшей математики. 38. Издательство Кембриджского университета. ISBN 978-0-521-55987-4. МИСТЕР 1269324. OCLC 36131259.
Краткое резюме с приложениями:
- Кашивара, Масаки; Шапира, Пьер (2002), "Глава I. Гомологическая алгебра", Пучки на коллекторах, Grundlehren der Mathematischen Wissenschaften, Springer-Verlag, Дои:10.1007/978-3-662-02661-8, ISBN 978-3540518617, МИСТЕР 1074006
Еще несколько дополнительных ссылок:
- Бейлинсон, А.А.; Бернштейн, Дж.; Делинь, П. (2018) [1982], "Faisceaux Pervers", Astérisque, Société Mathématique de France, Париж, 100, ISBN 978-2-85629-878-7, МИСТЕР 0751966
- Даггер, Дэниел; Шипли, Брук (2009), «Любопытный пример триангулированных эквивалентных категорий моделей, которые не являются эквивалентами Квиллена», Алгебраическая и геометрическая топология, 9: 135–166, arXiv:0710.3070, Дои:10.2140 / agt.2009.9.135, МИСТЕР 2482071
- Хартсхорн, Робин (1966), "Глава I. Производная категория", Остатки и двойственность, Конспект лекций по математике 20, Springer-Verlag, стр. 20–48, Дои:10.1007 / BFb0080482, ISBN 978-3-540-03603-6, МИСТЕР 0222093
- Краузе, Хеннинг (2010), "Теория локализации для триангулированных категорий", Триангулированные категории, Серия лекций Лондонского математического общества, 375, Cambridge University Press, стр. 161–235, arXiv:0806.1324, Дои:10.1017 / CBO9781139107075.005, МИСТЕР 2681709
- Neeman, Amnon (1996), "Теорема двойственности Гротендика через методы Боусфилда и представимость Брауна", Журнал Американского математического общества, 9: 205–236, Дои:10.1090 / S0894-0347-96-00174-9, МИСТЕР 1308405
- Нееман, Амнон (2001), Триангулированные категории, Annals of Mathematics Studies, Princeton University Press, Дои:10.1515/9781400837212, ISBN 978-0691086866, МИСТЕР 1812507
- Puppe, Дитер (1962), "О формальной структуре стабильной теории гомотопий", Коллоквиум по алгебраической топологии, Математический институт Орхусского университета, стр. 65–71, Zbl 0139.41106
- Puppe, Дитер (1967), "Stabile Homotopietheorie. I.", Mathematische Annalen, 169: 243–274, Дои:10.1007 / BF01362348, МИСТЕР 0211400
- Равенел, Дуглас (1992), Нильпотентность и периодичность в стабильной теории гомотопий, Издательство Принстонского университета, ISBN 9780691025728, МИСТЕР 1192553
- Риццардо, Алиса; Ван ден Берг, Мишель; Neeman, Amnon (2019), «Пример не-Фурье-Мукаи функтора между производными категориями когерентных пучков», Inventiones Mathematicae, 216: 927–1004, arXiv:1410.4039, Дои:10.1007 / s00222-019-00862-9, МИСТЕР 3955712
- Тоен, Бертран (2007), «Гомотопическая теория dg-категорий и производная теория Морита», Inventiones Mathematicae, 167: 615–667, arXiv:математика / 0408337, Дои:10.1007 / s00222-006-0025-у, МИСТЕР 2276263
- Вердье, Жан-Луи (1977) [1963], "Деривированные категории: результаты исследований (état 0)", Cohomologie étale (SGA 41⁄2) (PDF), Конспект лекций по математике, 569, Springer, стр. 262–311, Дои:10.1007 / BFb0091525, ISBN 978-3-540-08066-4, МИСТЕР 3727440
- Вердье, Жан-Луи (1996) [1967], Des derivées derivées категорий abéliennes, Astérisque, 239, Société Mathématique de France, МИСТЕР 1453167
внешняя ссылка
- Дж. Питер Мэй, Аксиомы для триангулированных категорий
- Авторы проекта Stacks, The Stacks Project


![{ Displaystyle X [n] = Sigma ^ {n} X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08610d4aeee037672d8990b22933f4f76275179e)


![{ displaystyle w двоеточие Z к X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd0e1f46d0d9e4dda8d4d848dd1fa2cfab99a99e)
![{ Displaystyle X { xrightarrow {{} на вершине u}} Y { xrightarrow {{} на вершине v}} Z { xrightarrow {{} на вершине w}} X [1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d080709e649a0dc708fa1b07e8b4a57f296962df)

![{ displaystyle X { overset { text {id}} { to}} от X до 0 до X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17432691375f4c21be7690c6022e62271e0c37f5)
![{ Displaystyle X { xrightarrow {{} на вершине u}} от Y до Z до X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19d09ed580db17fa48bb1673a87d38e720445b97)

![{ Displaystyle X { xrightarrow {{} на вершине u}} Y { xrightarrow {{} на вершине v}} Z { xrightarrow {{} на вершине w}} X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbbac0e050cd6b115db02f6199ee220d36fb98ae)



![X '{ xrightarrow {guf ^ {{- 1}}}} Y' { xrightarrow {hvg ^ {{- 1}}}} Z '{ xrightarrow {f [1] wh ^ {{- 1}} }} X '[1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/86a457dcaf9a6f125a9bdec78ab8233ebe147ea5)
![{ Displaystyle Y { xrightarrow {{} на вершине v}} Z { xrightarrow {{} atop w}} X [1] { xrightarrow {-u [1]}} Y [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceafad558b94cffb57c6a3e8579a3fb02b0408ef)
![{ displaystyle Z [-1] { xrightarrow {-w [-1]}} X { xrightarrow {{} atop u}} Y { xrightarrow {{} atop v}} Z. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b979f0004827be755d5f48d6ddbb5aea1fb0bf17)
![[1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)
![[-1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/300bcd57c1f4d5f6c3e2f30e42008a3c84692fb7)
![{ displaystyle -w [-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e75add6c4209a6031944d66d3ca57947b7fa69b0)
![{ displaystyle Z [-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40456f93a60f65920a122a9882c7f7bf7a2d0351)
![{ Displaystyle (Х [1]) [- 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0dbad379d95045a74aff1cd59dc914544711dd8)
![[ИКС]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)
![{ displaystyle (X [1]) [- 1] { xrightarrow {}} X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/941f656437379b23d3b962fc3161408198994f51)


![{ displaystyle X { xrightarrow {u ,}} Y { xrightarrow {j}} Z '{ xrightarrow {k}} X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f158ae7293f1b53a9a60dcd05d9a9010237adb)
![{ Displaystyle Y { xrightarrow {v ,}} Z { xrightarrow {l}} X '{ xrightarrow {i}} Y [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2fafd394fe33e7d79af3887ef7d540c3d374f81)
![{ displaystyle X { xrightarrow {{} atop vu}} Z { xrightarrow {m}} Y '{ xrightarrow {n}} X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/552456ffc918cdc5d853061de0aea35ce82d16ca)
![{ displaystyle Z '{ xrightarrow {f}} Y' { xrightarrow {g}} X '{ xrightarrow {h}} Z' [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b771b4607151049622e907ebf3001eeab218141e)
![l = gm, quad k = nf, quad h = j [1] i, quad ig = u [1] n, quad fj = mv.](https://wikimedia.org/api/rest_v1/media/math/render/svg/83096d22d209b98bb9ebc59f212b2ceafd2b3b2a)












![{ Displaystyle от X к Y к Z к X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/588349d16ba4e081a8dc9a11f281b22e2eadc598)

![{ displaystyle { begin {matrix} R & to & 0 & to & R [+1] & to downarrow && downarrow &&& 0 & to & R [+1] & to & R [+1] & to end {matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20823feebf08901d8e44a6ccbd20a2d442ba6847)

![{ displaystyle { begin {align} { text {id}}: & R [+1] to R [+1] 0: & R [+1] to R [+1] end {выровнено} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebede7fff9b9fed15a68ec19e94f844f23740c63)


![{ displaystyle X to Y to { text {cone}} (f) to X [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79aa018e899a49107d2f0d1b8d94e352f1d2a7f1)
















![{ Displaystyle X к Y к Z к X [1], }](https://wikimedia.org/api/rest_v1/media/math/render/svg/590467d2035f7af35f5cc26fb4db1b16519b20d2)

![{ Displaystyle cdots к Z [-1] к X к Y к Z к X [1] к cdots, }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba09b21e0cc73f8189f10761f8963262d42ca888)
![{ Displaystyle cdots к F (Z [-1]) к F (X) к F (Y) к F (Z) к F (X [1]) к cdots. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/69d728735c719086dfe9d1a053dccbb36877d6c5)


![{ displaystyle cdots to operatorname {Hom} (B, X [i]) to operatorname {Hom} (B, Y [i]) to operatorname {Hom} (B, Z [i]) to operatorname {Hom} (B, X [i + 1]) to cdots}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18b72fdfde4ad75107902bce586659d7ef547a73)
![{ displaystyle cdots to operatorname {Hom} (Z, B [i]) to operatorname {Hom} (Y, B [i]) to operatorname {Hom} (X, B [i]) to operatorname {Hom} (Z, B [i + 1]) to cdots.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c6ff9644bfdee8c378ad2933992d55148464e72)
![{ displaystyle operatorname {Ext} ^ {i} (B, X) = operatorname {Hom} (B, X [i])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d753c4e47c464cac8215d1fcbfcb12a628c004bf)



![{ Displaystyle H ^ {0} (X [я]) cong H ^ {я} (X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c10462496314eefead7ffa1259b8bbcbfa5933eb)


![F (X) { xrightarrow {F (u)}} F (Y) { xrightarrow {F (v)}} F (Z) { xrightarrow { eta _ {X} F (w)}} F ( X) [1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c790de2fe6d10b9b2dc21b41d3d2e5384ba05851)





![{ Displaystyle Y [п] к X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b9312740eedb089a2cd42030302366a58a59ba4)






![{ Displaystyle от Y к X к LX к Y [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b820c7abb11d3e52553938399ff900d34c954ba9)

