Конверт (математика) - Envelope (mathematics)

Огибающую колебательного сигнала см. Конверт (волны). Относительно абстрактной концепции см. Конверт (теория категорий).

Построение огибающей семейства кривых.

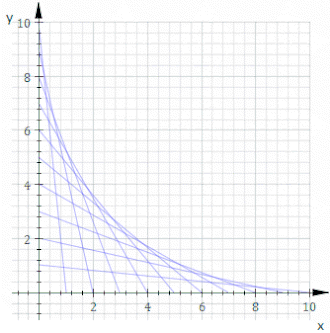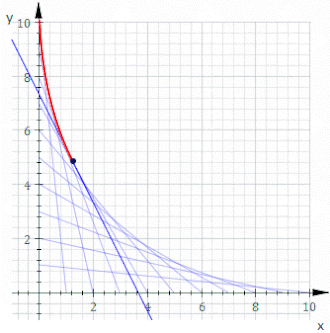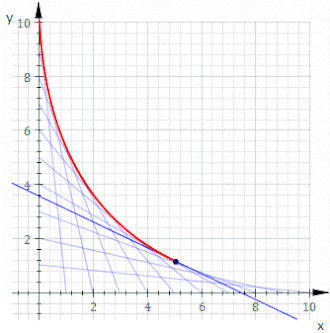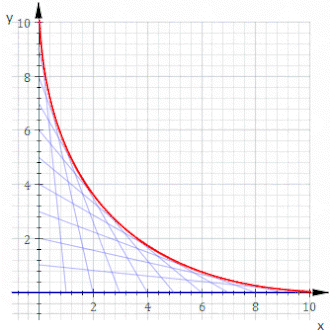
В геометрия, конверт плоского семейство кривых это изгиб то есть касательная каждому члену семьи в какой-то момент, и эти точки касания вместе образуют всю оболочку. Классически точку на конверте можно представить как пересечение двух "бесконечно мало смежные кривые, означающие предел пересечений соседних кривых. Эта идея может быть обобщенный в конверт из поверхности в космосе и так далее до более высоких измерений.

Чтобы иметь конверт, необходимо, чтобы отдельные члены семейства кривых были дифференцируемые кривые поскольку иначе понятие касания не применяется, и должен быть гладкий переход, происходящий через участников. Но этих условий недостаточно - у данной семьи может не быть конверта. Простым примером этого является семейство концентрических кругов расширяющегося радиуса.

Огибающая семейства кривых

Пусть каждая кривая C_т в семействе задается как решение уравнения ж_т(Икс, у) = 0 (см. неявная кривая ), куда т является параметром. Написать F(т, Икс, у)=ж_т(Икс, у) и предположим F дифференцируема.

Конверт семьи C_т тогда определяется как множество ${\displaystyle {\mathcal {D}}}$ точек (Икс,у), для которых одновременно

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0}$

за некоторую стоимость т,куда ${\displaystyle \partial F/\partial t}$ это частная производная из F относительно т.^[1]

Если т и ты, т≠ты - два значения параметра, то пересечение кривых C_т и C_ты дан кем-то

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

или, что то же самое,

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.}$

Устремление u → t дает определение выше.

Важный частный случай - это когда F(т, Икс, у) - многочлен от т. Это включает, по расчетные знаменатели, случай, когда F(т, Икс, у) - рациональная функция от т. В этом случае определение сводится к т быть двойным корнем F(т, Икс, у), поэтому уравнение огибающей можно найти, задав дискриминант из F до 0 (потому что определение требует F = 0 при некотором t и первой производной = 0, то есть его значение 0, и это min / max при этом t).

Например, пусть C_т быть линией, чья Икс и у перехваты т и 11−т, это показано на анимации выше. Уравнение C_т является

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

или, очищая фракции,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

Уравнение конверта тогда

${\displaystyle (-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,}$

Часто когда F не является рациональной функцией параметра, его можно свести к этому случаю соответствующей заменой. Например, если семья представлена C_θ с уравнением вида ты(Икс, у) cosθ +v(Икс, у) sinθ =ш(Икс, у), затем положив т=е^яθ, cosθ = (т+1/т) / 2, sinθ = (т-1/т)/2я изменяет уравнение кривой на

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

или же

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

Уравнение огибающей задается установкой дискриминанта на 0:

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

или же

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Альтернативные определения

1. Конверт E₁ предел пересечений близких кривых C_т.
2. Конверт E₂ кривая, касательная ко всем C_т.
3. Конверт E₃ - граница области, заполненной кривыми C_т.

потом ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$, ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ и ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$, куда ${\displaystyle {\mathcal {D}}}$ - это набор точек, определенных в начале родительского раздела этого подраздела.

Примеры

Пример 1

Эти определения E₁, E₂, и E₃ Из конверта могут быть разные наборы. Рассмотрим, например, кривую у = Икс³ параметризовано γ: р → р² куда γ (т) = (т,т³). Однопараметрическое семейство кривых будет задано касательными к γ.

Сначала вычисляем дискриминант ${\displaystyle {\mathcal {D}}}$. Производящая функция

${\displaystyle F(t,(x,y))=3t^{2}x-y-2t^{3}.}$

Вычисление частной производной F_т = 6т(Икс – т). Отсюда следует, что либо Икс = т или же т = 0. Сначала предположим, что Икс = т и т ≠ 0. Подставляя в F: ${\displaystyle F(t,(t,y))=t^{3}-y\,}$и так, предполагая, что т ≠ 0, следует, что F = F_т = 0 если и только если (Икс,у) = (т,т³). Далее, предполагая, что т = 0 и подставив в F дает F(0,(Икс,у)) = −у. Итак, если предположить т = 0, следует, что F = F_т = 0 если и только если у = 0. Таким образом, дискриминант - это исходная кривая и касательная к ней в точке γ (0):

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

Далее мы вычисляем E₁. Одна кривая задается F(т,(Икс,у)) = 0 и ближайшая кривая задается F(т + ε, (Икс,у)) где ε - какое-то очень маленькое число. Точка пересечения получается, если смотреть на предел F(т,(Икс,у)) = F(т + ε, (Икс,у)) при стремлении ε к нулю. Заметь F(т,(Икс,у)) = F(т + ε, (Икс,у)) если и только если

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Если т ≠ 0 тогда L имеет только один множитель ε. При условии, что т ≠ 0 то пересечение задается формулой

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .}$

С т ≠ 0 следует, что Икс = т. В у значение рассчитывается, зная, что эта точка должна лежать на касательной к исходной кривой γ: F(т,(Икс,у)) = 0. Подстановка и решение дают у = т³. Когда т = 0, L делится на ε². При условии, что т = 0 то пересечение задается формулой

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

Следует, что Икс = 0, и зная, что F(т,(Икс,у)) = 0 дает у = 0. Следует, что

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Далее мы вычисляем E₂. Сама кривая - это кривая, касательная ко всем своим касательным линиям. Следует, что

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Наконец, мы вычисляем E₃. Каждая точка на плоскости имеет по крайней мере одну касательную к γ, проходящую через нее, поэтому область, заполненная касательными линиями, составляет всю плоскость. Граница E₃ следовательно, пустое множество. Действительно, рассмотрим точку на плоскости, скажем (Икс₀,у₀). Эта точка лежит на касательной тогда и только тогда, когда существует т такой, что

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

Это кубик в т и поэтому имеет по крайней мере одно реальное решение. Отсюда следует, что хотя бы одна касательная к γ должна проходить через любую заданную точку на плоскости. Если у > Икс³ и у > 0 затем каждая точка (Икс,у) имеет ровно одну касательную к γ, проходящую через него. То же верно, если у < Икс³ у < 0. Если у < Икс³ и у > 0 затем каждая точка (Икс,у) имеет ровно три различные касательные к γ, проходящие через него. То же верно, если у > Икс³ и у < 0. Если у = Икс³ и у ≠ 0 затем каждая точка (Икс,у) имеет ровно две касательные к γ, проходящие через него (это соответствует кубике, имеющей один обычный корень и один повторяющийся корень). То же верно, если у ≠ Икс³ и у = 0. Если у = Икс³ и Икс = 0, т.е. Икс = у = 0, то через эту точку проходит единственная касательная к γ (это соответствует кубике, имеющей один действительный корень кратности 3). Следует, что

${\displaystyle E_{3}=\varnothing .}$

Пример 2

Этот график дает огибающую семейства линий, соединяющих точки (т,0), (0,k - т), в котором k принимает значение 1.

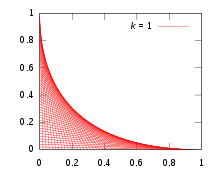
В струнное искусство Обычно перекрестно соединяют две линии с одинаковыми выводами. Какая кривая образуется?

Для простоты установите штифты на Икс- и у-оси; не-ортогональный макет - это вращение и масштабирование прочь. Общая прямолинейная резьба соединяет две точки (0, k−т) и (т, 0), где k - произвольная константа масштабирования, а семейство линий генерируется изменением параметра т. Исходя из простой геометрии, уравнение этой прямой имеет вид у = −(k − т)Икс/т + k − т. Перестановка и приведение в форму F(Икс,у,т) = 0 дает:

${\displaystyle F(x,y,t)=-{\frac {kx}{t}}-t+x+k-y=0\,}$

(1)

Теперь дифференцируйте F(Икс,у,т) относительно т и установите результат равным нулю, чтобы получить

${\displaystyle {\frac {\partial F(x,y,t)}{\partial t}}={\frac {kx}{t^{2}}}-1=0\,}$

(2)

Эти два уравнения совместно определяют уравнение огибающей. Из (2) имеем:

${\displaystyle t={\sqrt {kx}}\,}$

Подставляя это значение т в (1) и упрощение дает уравнение для огибающей:

${\displaystyle y=({\sqrt {x}}-{\sqrt {k}})^{2}\,}$

(3)

Или, преобразовав в более элегантную форму, которая показывает симметрию между x и y:

${\displaystyle {\sqrt {x}}+{\sqrt {y}}={\sqrt {k}}}$

(4)

Мы можем взять вращение осей, где б ось это линия у = х ориентированный на северо-восток и а ось это линия y = -x ориентирован на юго-восток. Эти новые топоры связаны с оригинальными х-у топоры х = (Ь + а) /√2 и у = (б-а) /√2 . После подстановки в (4) и разложения и упрощения получаем

${\displaystyle b={\frac {1}{k{\sqrt {2}}}}a^{2}+{\frac {k}{2{\sqrt {2}}}}}$,

(5)

что, по-видимому, является уравнением параболы с осью вдоль а = 0, или же у = х.

Пример 3

Позволять я ⊂ р - открытый интервал, и пусть γ: я → р² - гладкая плоская кривая, параметризованная длина дуги. Рассмотрим однопараметрическое семейство нормальных прямых к γ (я). Прямая нормальна к γ в точке γ (т), если он проходит через γ (т) и перпендикулярна касательный вектор к γ в точке γ (т). Позволять Т обозначим единичный касательный вектор к γ и пусть N обозначим единицу нормальный вектор. Использование точки для обозначения скалярное произведение, порождающее семейство для однопараметрического семейства нормальных прямых имеет вид F : я × р² → р куда

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Четко (Икс - γ) ·Т = 0 тогда и только тогда, когда Икс - γ перпендикулярно Т, или, что то же самое, тогда и только тогда, когда Икс - γ есть параллельно к N, или, что то же самое, тогда и только тогда, когда Икс = γ + λN для некоторого λ ∈ р. Следует, что

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}}$

- в точности нормальная прямая к γ в точке γ (т₀). Чтобы найти дискриминант F нам нужно вычислить его частную производную по т:

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,}$

где κ - кривизна кривой плоскости из γ. Было замечено, что F = 0 тогда и только тогда, когда Икс - γ = λN для некоторого λ ∈ р. При условии, что F = 0 дает

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

Если предположить, что κ ≠ 0, то λ = 1 / κ и, значит,

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

Это именно та эволюционировать кривой γ.

Пример 4

An астроид как огибающую семейства прямых, соединяющих точки (s,0), (0,т) с s² + т² = 1

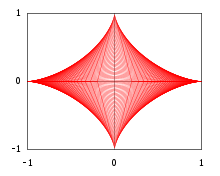
Следующий пример показывает, что в некоторых случаях оболочка семейства кривых может рассматриваться как топологическая граница объединения множеств, границы которых являются кривыми оболочки. За ${\displaystyle s>0}$ и ${\displaystyle t>0}$ рассмотрим (открытый) прямоугольный треугольник на декартовой плоскости с вершинами ${\displaystyle (0,0)}$, ${\displaystyle (s,0)}$ и ${\displaystyle (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.}$

Зафиксируйте показатель степени ${\displaystyle \alpha >0}$, и рассмотрим объединение всех треугольников ${\displaystyle T_{s,t}}$ подвергнутый принуждению ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$, то есть открытое множество

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Чтобы написать декартово представление для ${\displaystyle \textstyle \Delta _{\alpha }}$, начнем с любого ${\displaystyle \textstyle s>0}$, ${\displaystyle \textstyle t>0}$ удовлетворение ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$ и любой ${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$. В Неравенство Гёльдера в ${\displaystyle \textstyle \mathbb {R} ^{2}}$ относительно сопряженных показателей ${\displaystyle p:=1+{\frac {1}{\alpha }}}$ и ${\displaystyle \textstyle q:={1+\alpha }}$ дает:

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}}$,

с равенством тогда и только тогда, когда ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$В терминах объединения множеств последнее неравенство читается так: точка ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ принадлежит набору ${\displaystyle \textstyle \Delta _{\alpha }}$, то есть принадлежит какому-то ${\displaystyle \textstyle T_{s,t}}$ с ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$, тогда и только тогда, когда он удовлетворяет

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

Более того, граница в ${\displaystyle \mathbb {R} _{+}^{2}}$ из набора ${\displaystyle \textstyle \Delta _{\alpha }}$ является оболочкой соответствующего семейства отрезков прямых

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(то есть гипотенузы треугольников) и имеет декартово уравнение

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

Обратите внимание, что, в частности, значение ${\displaystyle \alpha =1}$ дает дугу параболы из примера 1, а значение ${\displaystyle \alpha =2}$ (что означает, что все гипотенузы являются отрезками единичной длины) дает астроид.

Пример 5

Огибающая орбит снарядов (с постоянной начальной скоростью) представляет собой вогнутую параболу. Начальная скорость 10 м / с. Мы принимаем грамм = 10 м / с².

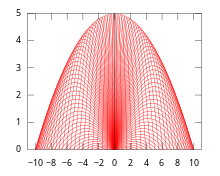
Рассмотрим следующий пример конверта в движении. Предположим, что на начальной высоте 0 бросается снаряд в воздух с постоянной начальной скоростью v но разные углы возвышения θ. Позволять Икс - горизонтальная ось на поверхности движения, и пусть у обозначают вертикальную ось. Тогда движение дает следующий дифференциал динамическая система:

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,}$

который удовлетворяет четырем первоначальные условия:

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Здесь т обозначает время движения, θ - угол места, грамм обозначает гравитационное ускорение, и v постоянная начальная скорость (не скорость ). Решение вышеуказанной системы может занять неявная форма:

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.}$

Чтобы найти уравнение огибающей, можно вычислить желаемую производную:

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

Исключив θ, можно получить следующее уравнение огибающей:

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Очевидно, что полученный конверт также является вогнутый парабола.

Огибающая семейства поверхностей

А однопараметрическое семейство поверхностей в трехмерном евклидовом пространстве задается системой уравнений

${\displaystyle F(x,y,z,a)=0}$

в зависимости от реального параметра а.^[2] Например, касательные плоскости к поверхности вдоль кривой поверхности образуют такое семейство.

Две поверхности, соответствующие разным значениям а и а ' пересекаются по общей кривой, определяемой

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.}$

В пределе как а ' подходы а, эта кривая стремится к кривой, содержащейся на поверхности в точке а

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Эта кривая называется характеристика семьи в а. В качестве а варьирует геометрическое место этих характеристических кривых, определяет поверхность, называемую конверт семейства поверхностей.

Огибающая семейства поверхностей касается каждой поверхности в семействе вдоль характеристической кривой на этой поверхности.

Обобщения

Идея оболочки семейства гладких подмногообразий следует естественным образом. Вообще говоря, если у нас есть семейство подмногообразий коразмерности c то нам нужно иметь хотя бы c-параметрическое семейство таких подмногообразий. Например: однопараметрическое семейство кривых в трехпространстве (c = 2) в общем случае не имеет конверта.

Приложения

Обыкновенные дифференциальные уравнения

Конверты связаны с изучением обыкновенные дифференциальные уравнения (ODE), и в частности особые решения ODE.^[3] Рассмотрим, например, однопараметрическое семейство касательных к параболе у = Икс². Они даются производящей семьей F(т,(Икс,у)) = т² – 2tx + у. Набор нулевого уровня F(т₀,(Икс,у)) = 0 дает уравнение касательной к параболе в точке (т₀,т₀²). Уравнение т² – 2tx + у = 0 всегда можно решить для у как функция Икс Итак, рассмотрим

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

Подстановка

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

дает ODE

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

Не удивительно у = 2tx − т² все решения этого ODE. Однако огибающая этого однопараметрического семейства линий, представляющая собой параболу у = Икс², также является решением этого ODE. Другой известный пример: Уравнение Клеро.

Уравнения с частными производными

Конверты можно использовать для построения более сложных решений первого порядка. уравнения в частных производных (PDE) от более простых.^[4] Позволять F(Икс,ты, Dты) = 0 - УЧП первого порядка, где Икс - переменная со значениями в открытом множестве Ω ⊂р^п, ты - неизвестная вещественная функция, Dты это градиент из ты, и F - непрерывно дифференцируемая функция, регулярная в Dты. Предположим, что ты(Икс;а) является м-параметрическое семейство решений: то есть для каждого фиксированного а ∈ А ⊂ р^м, ты(Икс;а) является решением дифференциального уравнения. Новое решение дифференциального уравнения можно построить, предварительно решив (если возможно)

${\displaystyle D_{a}u(x;a)=0\,}$

за а = φ (Икс) как функция Икс. Оболочка семейства функций {ты(·,а)}_а∈А определяется

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

а также решает дифференциальное уравнение (при условии, что оно существует как непрерывно дифференцируемая функция).

Геометрически график v(Икс) всюду касается графика некоторого члена семейства ты(Икс;а). Поскольку дифференциальное уравнение имеет первый порядок, оно накладывает условие только на касательную плоскость к графику, так что любая функция, всюду касающаяся решения, также должна быть решением. Эта же идея лежит в основе решения уравнения первого порядка как интеграла от Конус Монжа.^[5] Конус Монжа - это поле конусов в р^п+1 из (Икс,ты) переменные, вырезанные оболочкой касательных пространств к УЧП первого порядка в каждой точке. Решение PDE тогда является огибающей поля конуса.

В Риманова геометрия, если гладкая семья геодезические через точку п в Риманово многообразие есть конверт, тогда п имеет сопряженная точка где любая геодезическая семейства пересекает оболочку. То же самое верно и в целом в вариационное исчисление: если семейство экстремалей к функционалу через заданную точку п имеет оболочку, то точка, в которой экстремаль пересекает оболочку, является точкой, сопряженной с п.

Каустики

Отражающая каустика, генерируемая круг и параллельные лучи

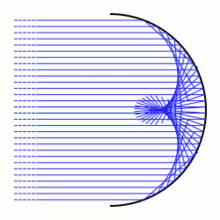
В геометрическая оптика, а едкий конверт семьи лучи света. На этой картинке есть дуга круга. Световые лучи (показаны синим цветом) исходят от источника в бесконечности, и так поступают параллельно. Когда они попадают в дугу окружности, световые лучи рассеиваются в разных направлениях в зависимости от закон отражения. Когда луч света попадает на дугу в точке, свет будет отражаться так, как если бы он был отражен от дуги. касательная линия в таком случае. Отраженные световые лучи дают однопараметрическое семейство линий на плоскости. Конверт этих строк и есть отражающая каустика. Отражающая каустика обычно состоит из гладкий очки и обыкновенный куспид точки.

С точки зрения вариационного исчисления, Принцип Ферма (в его современном виде) подразумевает, что лучи света являются экстремалями для функционала длины

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

среди гладких кривых γ на [а,б] с фиксированными концами γ (а) и γ (б). Каустика, определяемая данной точкой п (на изображении точка находится на бесконечности) - это множество точек, сопряженных с п.^[6]

Принцип Гюйгенса

Свет может проходить через анизотропные неоднородные среды с разной скоростью в зависимости от направления и начального положения светового луча. Граница множества точек, в которые свет может перемещаться из данной точки. q через время т известен как фронт волны по истечении времени т, обозначаемый здесь Φ_q(т). Он состоит именно из точек, до которых можно добраться из q во время т путешествуя со скоростью света. Принцип Гюйгенса утверждает, что фронт волны установлен Φ_q0(s + т) является огибающей семейства волновых фронтов Φ_q(s) за q ∈ Φ_q0(т). В общем, суть q₀ может быть заменен любой кривой, поверхностью или замкнутым множеством в пространстве.^[7]

Смотрите также

• Линейчатая поверхность
• Каустик (математика)

Рекомендации

1. Брюс, Дж. У .; Гиблин, П. Дж. (1984), Кривые и особенности, Издательство Кембриджского университета, ISBN  0-521-42999-4
2. Эйзенхарт, Лютер П. (2008), Трактат о дифференциальной геометрии кривых и поверхностей, Schwarz Press, ISBN  1-4437-3160-9
3. Форсайт, Эндрю Рассел (1959), Теория дифференциальных уравнений, Шесть томов в трех переплетах, Нью-Йорк: Dover Publications, МИСТЕР  0123757, §§100-106.
4. Эванс, Лоуренс К. (1998), Уравнения с частными производными, Провиденс, Р.И.: Американское математическое общество, ISBN  978-0-8218-0772-9.
5. Джон, Фриц (1991), Уравнения с частными производными (4-е изд.), Springer, ISBN  978-0-387-90609-6.
6. Родился, Макс (Октябрь 1999 г.), Принцип оптики, Издательство Кембриджского университета, ISBN  978-0-521-64222-4, Приложение I: Вариационное исчисление.
7. Арнольд, В.И. (1997), Математические методы классической механики, 2-е изд., Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-96890-2, §46.

внешняя ссылка

• Конверт (математика) на Британская энциклопедия
• Вайсштейн, Эрик В. "Конверт". MathWorld.
• «Огибающая семейства плоских кривых» в MathCurve.