Динамическая система - Dynamical system

В Аттрактор Лоренца возникает при изучении Осциллятор Лоренца, динамическая система.

В математика, а динамическая система это система, в которой функция описывает время зависимость от точка в геометрическое пространство. Примеры включают математические модели которые описывают качание часов маятник, поток воды в трубе, и количество рыб в озере каждую весну.

В любой момент времени динамическая система имеет государственный данный кортеж из действительные числа (а вектор ), который можно представить точкой в соответствующем пространство состояний (геометрический многообразие ). В правило эволюции динамической системы - это функция, которая описывает, какие будущие состояния следуют из текущего состояния. Часто функция детерминированный, то есть для заданного временного интервала только одно будущее состояние следует из текущего состояния.^[1]^[2] Однако некоторые системы стохастический, в этом случае случайные события также влияют на эволюцию переменных состояния.

В физика, а динамическая система описывается как «частица или ансамбль частиц, состояние которых изменяется во времени и, таким образом, подчиняется дифференциальным уравнениям, включающим производные по времени».^[3] Чтобы сделать прогноз относительно будущего поведения системы, реализуется аналитическое решение таких уравнений или их интегрирование с течением времени посредством компьютерного моделирования.

Изучение динамических систем находится в центре внимания теория динамических систем, который может применяться в самых разных областях, таких как математика, физика,^[4]^[5] биология,^[6] химия, инженерное дело,^[7] экономика,^[8] история, и лекарство. Динамические системы являются фундаментальной частью теория хаоса, логистическая карта динамика теория бифуркации, то самосборка и самоорганизация процессы, а край хаоса концепция.

Обзор

Концепция динамической системы берет свое начало в Ньютоновская механика. Здесь, как и в других естественных и инженерных дисциплинах, правило эволюции динамических систем является неявным отношением, которое дает состояние системы только на короткое время в будущем. (Отношение либо дифференциальное уравнение, разностное уравнение или другой шкала времени.) Чтобы определить состояние для всех будущих времен, требуется многократное повторение соотношения - каждое время опережения представляет собой небольшой шаг. Итерационная процедура называется решение системы или же интеграция системы. Если система может быть решена, то с учетом начальной точки можно определить все ее будущие позиции, набор точек, известный как траектория или же орбита.

До появления компьютеры поиск орбиты требовал сложных математических методов и мог быть выполнен только для небольшого класса динамических систем. Численные методы, реализованные на электронных вычислительных машинах, упростили задачу определения орбит динамической системы.

Для простых динамических систем часто бывает достаточно знания траектории, но большинство динамических систем слишком сложны, чтобы их можно было понять в терминах отдельных траекторий. Сложности возникают из-за:

Изучаемые системы могут быть известны только приблизительно - параметры системы могут быть неизвестны точно или члены могут отсутствовать в уравнениях. Используемые приближения ставят под сомнение обоснованность или актуальность численных решений. Чтобы ответить на эти вопросы, при изучении динамических систем было введено несколько понятий устойчивости, таких как Ляпуновская устойчивость или же структурная устойчивость. Устойчивость динамической системы подразумевает, что существует класс моделей или начальных условий, для которых траектории были бы эквивалентными. Операция сравнения орбит для определения их эквивалентность меняется с разными представлениями о стабильности.
Тип траектории может быть важнее одной конкретной траектории. Некоторые траектории могут быть периодическими, тогда как другие могут блуждать по множеству различных состояний системы. Приложения часто требуют перечисления этих классов или поддержки системы в пределах одного класса. Классификация всех возможных траекторий привела к качественному изучению динамических систем, то есть свойств, которые не меняются при изменении координат. Линейные динамические системы и системы, у которых есть два числа, описывающих состояние являются примерами динамических систем, в которых понятны возможные классы орбит.
Поведение траекторий как функция параметра может быть тем, что требуется для приложения. При изменении параметра динамические системы могут иметь точки бифуркации где качественное поведение динамической системы меняется. Например, он может перейти от периодических движений к явно неустойчивому поведению, как в переход к турбулентности жидкости.
Траектории системы могут казаться беспорядочными, как бы случайными. В этих случаях может потребоваться вычисление средних значений с использованием одной очень длинной траектории или множества различных траекторий. Средние хорошо определены для эргодические системы и более детальное понимание было разработано для гиперболические системы. Понимание вероятностных аспектов динамических систем помогло установить основы статистическая механика и из хаос.

История

Многие считают французского математика Анри Пуанкаре как основоположник динамических систем.^[9] Пуанкаре опубликовал две, ставшие теперь классическими, монографии: «Новые методы небесной механики» (1892–1899) и «Лекции по небесной механике» (1905–1910). В них он успешно применил результаты своих исследований к проблеме движения трех тел и подробно изучил поведение решений (частота, устойчивость, асимптотика и т. Д.). Эти документы включали Теорема Пуанкаре о возвращении, в котором говорится, что определенные системы через достаточно долгое, но конечное время вернутся в состояние, очень близкое к исходному.

Александр Ляпунов разработал много важных методов приближения. Его методы, разработанные им в 1899 г., позволяют определять устойчивость систем обыкновенных дифференциальных уравнений. Он создал современную теорию устойчивости динамической системы.

В 1913 г. Джордж Дэвид Биркофф доказал Пуанкаре "Последняя геометрическая теорема ", частный случай проблема трех тел, результат, который сделал его всемирно известным. В 1927 году он опубликовал Динамические системы. Самым надежным результатом Биркгофа стало его открытие в 1931 году того, что сейчас называется эргодическая теорема. Объединение идей от физика на эргодическая гипотеза с теория меры, эта теорема решила, по крайней мере в принципе, фундаментальную проблему статистическая механика. Эргодическая теорема также повлияла на динамику.

Стивен Смейл также добились значительных успехов. Его первым вкладом был Подкова Смейла это послужило толчком к значительным исследованиям динамических систем. Он также изложил исследовательскую программу, проводимую многими другими.

Александр Николаевич Шарковский развитый Теорема шарковского на периоды дискретные динамические системы в 1964 году. Одно из следствий теоремы состоит в том, что если дискретная динамическая система на реальная линия имеет периодическая точка периода 3, то в нем должны быть периодические точки любого другого периода.

В конце 20 века палестинский инженер-механик Али Х. Найфех применяемый нелинейная динамика в механический и инженерное дело системы.^[10] Его новаторская работа в прикладной нелинейной динамике оказала влияние на создание и обслуживание машины и структуры которые распространены в повседневной жизни, например корабли, краны, мосты, здания, небоскребы, реактивные двигатели, ракетные двигатели, самолет и космический корабль.^[11]

Основные определения

Динамическая система - это многообразие M называется фазовым (или состоянием) пространством, наделенным семейством гладких эволюционных функций Φ^т что для любого элемента т ∈ Т, время, нанесите на карту точку фазовое пространство обратно в фазовое пространство. Понятие гладкости меняется в зависимости от приложений и типа многообразия. Есть несколько вариантов для набораТ. Когда Т принимается за действительные, динамическая система называется поток; и если Т ограничивается неотрицательными действительными числами, то динамическая система является полупоток. Когда Т принимается целыми числами, это каскад или карта; и ограничение на неотрицательные целые числа есть полукаскад.

Примечание. Существует еще одно техническое условие: Φ^т это действие Т на M. Сюда входят факты, что Φ⁰ - тождественная функция и что Φ^{с + т} композиция Φ^s и Φ^т. Это полугрупповое действие, что не требует наличия отрицательных значений для т, и не требует функций Φ^т быть обратимым.

Примеры

Функция эволюции Φ^т часто является решением дифференциальное уравнение движения

{displaystyle {dot {x}} = v (x).}

Уравнение дает производную по времени, обозначенную точкой, от траектории Икс(т) на фазовом пространстве, начиная с некоторой точкиИкс₀. В векторное поле v(Икс) - гладкая функция, которая в каждой точке фазового пространства M обеспечивает вектор скорости динамической системы в этой точке. (Эти векторы не являются векторами в фазовом пространствеM, но в касательное пространство Т_ИксM по делуИкс.) Для гладкого Φ^т, из него можно получить автономное векторное поле.

Нет необходимости ни в производных высшего порядка в уравнении, ни во временной зависимости в v(Икс), потому что их можно устранить, рассматривая системы более высоких измерений. Другие виды дифференциальные уравнения может использоваться для определения правила эволюции:

{displaystyle G (x, {точка {x}}) = 0}

это пример уравнения, возникающего в результате моделирования механических систем со сложными ограничениями.

Дифференциальные уравнения, определяющие эволюционную функцию Φ^т часто обыкновенные дифференциальные уравнения; в этом случае фазовое пространство M - конечномерное многообразие. Многие концепции динамических систем можно распространить на бесконечномерные многообразия, т.е. Банаховы пространства - в этом случае дифференциальные уравнения имеют вид уравнения в частных производных. В конце 20 века динамическая системная перспектива уравнений в частных производных начала набирать популярность.

Дальнейшие примеры

Линейные динамические системы

Линейные динамические системы могут быть решены в терминах простых функций и классификации поведения всех орбит. В линейной системе фазовое пространство - это N-мерное евклидово пространство, поэтому любая точка фазового пространства может быть представлена вектором с N числа. Анализ линейных систем возможен, поскольку они удовлетворяют принцип суперпозиции: если ты(т) и ш(т) удовлетворяют дифференциальному уравнению для векторного поля (но не обязательно начальному условию), то так будет ты(т) + ш(т).

Потоки

Для поток, векторное поле v (Икс) является аффинный функция положения в фазовом пространстве, то есть

{displaystyle {точка {x}} = v (x) = Ax + b,}

с А матрица, б вектор чисел и Икс вектор положения. Решение этой системы можно найти, используя принцип суперпозиции (линейности). б ≠ 0 с А = 0 - это просто прямая линия в направленииб:

{displaystyle Phi ^ {t} (x_ {1}) = x_ {1} + bt.}

Когда б равен нулю и А ≠ 0 начало координат является точкой равновесия (или особой точки) потока, т. Е. Если Икс₀ = 0, то орбита остается на месте. Для других начальных условий уравнение движения задается формулой экспонента матрицы: для начальной точки Икс₀,

{displaystyle Phi ^ {t} (x_ {0}) = e ^ {tA} x_ {0}.}

Когда б = 0, собственные значения из А определить структуру фазового пространства. Из собственных значений и собственные векторы из А можно определить, будет ли начальная точка сходиться или расходиться к точке равновесия в начале координат.

Расстояние между двумя разными начальными условиями в случае А 0 будет изменяться экспоненциально в большинстве случаев, либо экспоненциально быстро сходясь к точке, либо экспоненциально быстро расходясь. Линейные системы демонстрируют чувствительную зависимость от начальных условий в случае расхождения. Для нелинейных систем это одно из (необходимых, но не достаточных) условий для хаотичное поведение.

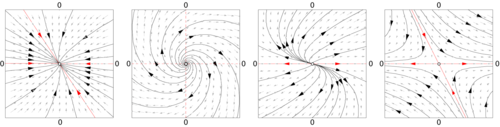
Линейные векторные поля и несколько траекторий.

Карты

А дискретное время, аффинный динамическая система имеет вид матричное разностное уравнение:

{displaystyle x_ {n + 1} = Ax_ {n} + b,}

с А матрица и б вектор. Как и в непрерывном случае, изменение координат Икс → Икс + (1 − А)^–1б убирает термин б из уравнения. В новом система координат, начало координат - неподвижная точка карты, а решения - линейной системы А^пИкс₀. Решения для карты больше не кривые, а точки, прыгающие в фазовом пространстве. Орбиты организованы в виде кривых или волокон, которые представляют собой наборы точек, которые отображаются сами в себя под действием карты.

Как и в непрерывном случае, собственные значения и собственные векторы А определить структуру фазового пространства. Например, если ты₁ является собственным вектором А, с действительным собственным значением меньше единицы, то прямые, заданные точками вдоль α ты₁, с α ∈ р, - инвариантная кривая отображения. Точки на этой прямой переходят в фиксированную точку.

Также много другие дискретные динамические системы.

Местная динамика

Качественные свойства динамических систем не меняются при плавном изменении координат (иногда это принимают за определение качественных): особая точка векторного поля (точка, гдеv(Икс) = 0) останется особой точкой при гладких преобразованиях; а периодическая орбита представляет собой петлю в фазовом пространстве, и плавные деформации фазового пространства не могут изменить ее как петлю. Именно в окрестностях особых точек и периодических орбит можно хорошо понять структуру фазового пространства динамической системы. В качественном исследовании динамических систем подход состоит в том, чтобы показать, что есть изменение координат (обычно неуказанное, но вычислимое), которое делает динамическую систему настолько простой, насколько это возможно.

Исправление

Поток в большинстве небольших участков фазового пространства можно сделать очень простым. Если у это точка, в которой векторное поле v(у) ≠ 0, то происходит смена координат области вокруг у где векторное поле становится серией параллельных векторов одинаковой величины. Это известно как теорема исправления.

В теорема исправления говорит, что вдали от особые точки динамика точки на небольшом участке - прямая линия. Патч иногда можно увеличить, сшив вместе несколько патчей, и когда это работает во всем фазовом пространстве M динамическая система интегрируемый. В большинстве случаев патч нельзя распространить на все фазовое пространство. В векторном поле могут быть особые точки (где v(Икс) = 0); или пятна могут становиться все меньше и меньше по мере приближения к какой-то точке. Более тонкая причина - это глобальное ограничение, когда траектория начинается в патче, а после посещения ряда других патчей возвращается к исходной. Если в следующий раз орбита будет обходить фазовое пространство по-другому, то исправить векторное поле во всей серии пятен будет невозможно.

Около периодических орбит

Вообще говоря, в окрестности периодической орбиты теорема исправления неприменима. Пуанкаре разработал подход, который преобразует анализ около периодической орбиты в анализ карты. Выберите точку Икс₀ на орбите γ и рассмотрим точки фазового пространства в этой окрестности, перпендикулярные v(Икс₀). Эти точки являются Раздел Пуанкаре S(γ, Икс₀) орбиты. Теперь поток определяет карту, Карта Пуанкаре F : S → S, для точек, начинающихся в S и возвращаясь кS. Не все эти точки будут возвращаться одинаково долго, но это время будет близко к тому времени, которое потребуетсяИкс₀.

Пересечение периодической орбиты с сечением Пуанкаре является неподвижной точкой отображения Пуанкаре F. Путем перевода можно предположить, что точка находится в Икс = 0. Ряд Тейлора отображения равен F(Икс) = J · Икс + O (Икс²), поэтому смена координат час можно только ожидать упрощения F к своей линейной части

{displaystyle h ^ {- 1} circ Fcirc h (x) = Jcdot x.}

Это известно как уравнение сопряжения. Поиск условий для выполнения этого уравнения был одной из основных задач исследования динамических систем. Пуанкаре первым подошел к нему, предполагая, что все функции аналитические, и в процессе обнаружил условие нерезонансности. Если λ₁, ..., λ_ν являются собственными значениями J они будут резонансными, если одно собственное значение является целочисленной линейной комбинацией двух или более других. Как условия формы λ_я - (кратное другим собственным значениям) входит в знаменатель членов функции час, условие нерезонансности также известно как проблема малых делителей.

Результаты конъюгации

Результаты о существовании решения уравнения сопряжения зависят от собственных значений J и степень гладкости, требуемая от час. В качестве J не требует особых симметрий, его собственные значения обычно являются комплексными числами. Когда собственные значения J не находятся в единичном круге, динамика вблизи фиксированной точки Икс₀ из F называется гиперболический а когда собственные значения находятся на единичном круге и комплексны, динамика называется эллиптический.

В гиперболическом случае Теорема Хартмана – Гробмана. дает условия существования непрерывной функции, отображающей окрестность неподвижной точки отображения в линейное отображение J · Икс. Гиперболический случай также структурно стабильный. Небольшие изменения в векторном поле вызовут только небольшие изменения в отображении Пуанкаре, и эти небольшие изменения будут отражаться в небольших изменениях положения собственных значений J в комплексной плоскости, что означает, что карта все еще гиперболическая.

В Колмогорова – Арнольда – Мозера (КАМ) Теорема дает поведение вблизи эллиптической точки.

Теория бифуркации

Когда эволюционное отображение Φ^т (или векторное поле он выводится из) зависит от параметра μ, структура фазового пространства также будет зависеть от этого параметра. Небольшие изменения могут не привести к качественным изменениям в фазовое пространство до особого значения μ₀ достигнуто. В этот момент фазовое пространство качественно меняется, и говорят, что динамическая система пережила бифуркацию.

Теория бифуркации рассматривает структуру в фазовом пространстве (обычно фиксированная точка, периодическая орбита или инвариант тор ) и изучает его поведение в зависимости от параметраμ. В точке бифуркации структура может изменить свою устойчивость, разделиться на новые структуры или слиться с другими структурами. Используя аппроксимацию карт рядами Тейлора и понимание различий, которые могут быть устранены путем изменения координат, можно каталогизировать бифуркации динамических систем.

Бифуркации гиперболической неподвижной точки Икс₀ системной семьи F_μ можно охарактеризовать собственные значения первой производной системы DF_μ(Икс₀), вычисленные в точке бифуркации. Для карты бифуркация произойдет, когда есть собственные значения DF_μ на единичном круге. Для потока это произойдет, когда на мнимой оси есть собственные значения. Для получения дополнительной информации см. Основную статью о Теория бифуркации.

Некоторые бифуркации могут привести к очень сложным структурам в фазовом пространстве. Например, Сценарий Рюэля – Такенса описывает, как периодическая орбита раздваивается на тор, а тор - на странный аттрактор. В другом примере Удвоение периода Фейгенбаума описывает, как устойчивая периодическая орбита проходит через серию бифуркации удвоения периода.

Эргодические системы

Во многих динамических системах можно выбрать координаты системы так, чтобы объем (на самом деле ν-мерный объем) в фазовом пространстве был инвариантным. Это происходит с механическими системами, выведенными из законов Ньютона, если координатами являются положение и импульс, а объем измеряется в единицах (положение) × (импульс). Поток берет точки подмножества А в точки Φ^т(А) и инвариантность фазового пространства означает, что

{displaystyle mathrm {vol} (A) = mathrm {vol} (Phi ^ {t} (A)).}

в Гамильтонов формализм По заданной координате можно получить соответствующий (обобщенный) импульс, при котором связанный объем сохраняется потоком. Говорят, что объем вычисляется Мера Лиувилля.

В гамильтоновой системе не все возможные конфигурации положения и импульса могут быть достигнуты из начального условия. Из-за сохранения энергии доступны только состояния с той же энергией, что и начальное условие. Состояния с одинаковой энергией образуют энергетическую оболочку Ω, подмногообразие фазового пространства. Объем энергетической оболочки, вычисленный с помощью меры Лиувилля, сохраняется при эволюции.

Для систем, в которых объем сохраняется потоком, Пуанкаре открыл теорема о возвращении: Предположим, что фазовое пространство имеет конечный лиувиллевский объем, и пусть F - карта, сохраняющая объем фазового пространства, и А подмножество фазового пространства. Тогда почти каждая точка А возвращается к А бесконечно часто. Теорема Пуанкаре о возвращении использовалась Цермело возражать против Больцман вывод увеличения энтропии в динамической системе сталкивающихся атомов.

Одним из вопросов, поднятых работой Больцмана, было возможное равенство между средними по времени и средними по пространству, то, что он назвал эргодическая гипотеза. Гипотеза гласит, что время, которое типичная траектория проводит в регионе А это объем (А) / объем (Ом).

Эргодическая гипотеза оказалась не самым важным свойством, необходимым для развития статистическая механика и ряд других свойств, подобных эргодике, были введены для отражения соответствующих аспектов физических систем. Купман подошел к изучению эргодических систем с помощью функциональный анализ. Наблюдаемый а представляет собой функцию, которая с каждой точкой фазового пространства связывает число (например, мгновенное давление или среднюю высоту). Значение наблюдаемой можно вычислить в другое время, используя функцию эволюции φ^т. Это вводит оператор U^т, то оператор передачи,

{displaystyle (U ^ {t} a) (x) = a (Phi ^ {- t} (x)).}

Изучая спектральные свойства линейного оператора U появляется возможность классифицировать эргодические свойства Φ^т. При использовании подхода Купмана, рассматривающего действие потока на наблюдаемую функцию, конечномерная нелинейная задача, включающая Φ^т отображается в бесконечномерную линейную задачу, включающуюU.

Мера Лиувилля, ограниченная энергетической поверхностью Ω, является основой для средних значений, вычисленных в равновесная статистическая механика. Среднее по времени вдоль траектории эквивалентно среднему по пространству, вычисленному с помощью Фактор Больцмана exp (−βЧАС). Эта идея была обобщена Синаем, Боуэном и Рюэлем (SRB) на более широкий класс динамических систем, который включает диссипативные системы. SRB меры заменяют фактор Больцмана, и они определяются на аттракторах хаотических систем.

Нелинейные динамические системы и хаос

Простые нелинейные динамические системы и даже кусочно-линейные системы могут демонстрировать совершенно непредсказуемое поведение, которое может показаться случайным, несмотря на то, что они по своей сути детерминированы. Это, казалось бы, непредсказуемое поведение было названо хаос. Гиперболические системы - это точно определенные динамические системы, которые проявляют свойства, приписываемые хаотическим системам. В гиперболических системах касательное пространство, перпендикулярное траектории, можно хорошо разделить на две части: одну с точками, сходящимися к орбите ( стабильное многообразие) и еще одна из точек, расходящихся с орбиты ( неустойчивый коллектор).

Эта ветвь математика имеет дело с долгосрочным качественным поведением динамических систем. Здесь основное внимание уделяется не поиску точных решений уравнений, определяющих динамическую систему (что часто безнадежно), а, скорее, ответам на такие вопросы, как «успокоится ли система. устойчивое состояние в долгосрочной перспективе, и если да, то каковы возможные аттракторы ? »или« Зависит ли долгосрочное поведение системы от ее начального состояния? »

Обратите внимание, что проблема не в хаотическом поведении сложных систем. Метеорология В течение многих лет известно, что оно связано со сложным - даже хаотичным - поведением. Теория хаоса была настолько удивительной, потому что хаос можно найти в почти тривиальных системах. В логистическая карта является полиномом только второй степени; то карта подковы кусочно-линейный.

Геометрическое определение

Динамическая система - это набор ${displaystyle langle {mathcal {M}}, f, {mathcal {T}} angle}$ , с ${displaystyle {mathcal {M}}}$ многообразие (локально банахово или евклидово пространство), ${displaystyle {mathcal {T}}}$ область для времени (неотрицательные действительные числа, целые числа, ...) и ж правило эволюции т → ж^т (с ${displaystyle tin {mathcal {T}}}$ ) такие, что ж^т это диффеоморфизм коллектора самому себе. Итак, f - отображение во временной области ${displaystyle {mathcal {T}}}$ в пространство диффеоморфизмов многообразия себе. Другими словами, ж(т) - диффеоморфизм, каждый раз т в домене ${displaystyle {mathcal {T}}}$ .

Измерьте теоретическое определение

Формально динамическую систему можно определить как сохраняющее меру преобразование сигма-алгебра, четверка (Икс, Σ, μ, τ). Здесь, Икс это набор, а Σ - сигма-алгебра на Икс, так что пара (Икс, Σ) - измеримое пространство. μ - конечная мера на сигма-алгебре, так что тройка (Икс, Σ, μ) является вероятностное пространство. Карта τ: Икс → Икс как говорят Σ-измеримый тогда и только тогда, когда для любого σ ∈ Σ выполняется ${displaystyle au ^ {- 1} сигма в сигме}$ . Отображение τ называется сохранить меру тогда и только тогда, когда для любого σ ∈ Σ выполняется ${displaystyle mu (au ^ {- 1} sigma) = mu (sigma)}$ . Объединяя вышесказанное, отображение τ называется сохраняющее меру преобразование Икс, если это карта из Икс для самого себя, оно Σ-измеримо и сохраняет меру. Четырехместный (Икс, Σ, μ, τ) для такого τ тогда определяется как динамическая система.

Карта τ воплощает эволюцию динамической системы во времени. Таким образом, для дискретных динамических систем повторяет ${displaystyle au ^ {n} = au circ au circ cdots circ au}$ для целого числа п изучаются. Для непрерывных динамических систем отображение τ понимается как отображение эволюции за конечное время, и конструкция более сложна.

Многомерное обобщение

Динамические системы определяются одной независимой переменной, обычно считающейся временем. Более общий класс систем определяется над несколькими независимыми переменными и поэтому называется многомерные системы. Такие системы полезны для моделирования, например, обработка изображений.

Смотрите также

дальнейшее чтение

Работы с широким охватом:

Ральф Абрахам и Джерролд Э. Марсден (1978). Основы механики. Бенджамин – Каммингс. ISBN 978-0-8053-0102-1. (доступно как переиздание: ISBN 0-201-40840-6)
Энциклопедия математических наук (ISSN 0938-0396 ) имеет подсерию по динамическим системам с обзорами текущих исследований.
Кристиан Бонатти; Лоренцо Х. Диас; Марсело Виана (2005). Динамика за пределами однородной гиперболичности: глобальная геометрическая и вероятностная перспектива. Springer. ISBN 978-3-540-22066-4.
Стивен Смейл (1967). «Дифференцируемые динамические системы». Бюллетень Американского математического общества. 73 (6): 747–817. Дои:10.1090 / S0002-9904-1967-11798-1.

Вступительные тексты с уникальной перспективой:

В. И. Арнольд (1982). Математические методы классической механики. Springer-Verlag. ISBN 978-0-387-96890-2.
Джейкоб Палис и Велингтон-де-Мело (1982). Геометрическая теория динамических систем: введение. Springer-Verlag. ISBN 978-0-387-90668-3.
Дэвид Рюэлль (1989). Элементы дифференцируемой динамики и теории бифуркаций. Академическая пресса. ISBN 978-0-12-601710-6.
Тим Бедфорд, Майкл Кин и Кэролайн Серии, ред. (1991). Эргодическая теория, символическая динамика и гиперболические пространства. Издательство Оксфордского университета. ISBN 978-0-19-853390-0.CS1 maint: несколько имен: список авторов (связь)
Ральф Х. Абрахам и Кристофер Д. Шоу (1992). Динамика - геометрия поведения, 2-е издание.. Эддисон-Уэсли. ISBN 978-0-201-56716-8.

Учебники

Кэтлин Т. Аллигуд, Тим Д. Зауэр и Джеймс А. Йорк (2000). Хаос. Введение в динамические системы. Springer Verlag. ISBN 978-0-387-94677-1.
Одед Галор (2011). Дискретные динамические системы. Springer. ISBN 978-3-642-07185-0.
Моррис В. Хирш, Стивен Смейл и Роберт Л. Девани (2003). Дифференциальные уравнения, динамические системы и введение в хаос. Академическая пресса. ISBN 978-0-12-349703-1.
Анатоль Каток; Борис Хассельблатт (1996). Введение в современную теорию динамических систем. Кембридж. ISBN 978-0-521-57557-7.
Стивен Линч (2010). Динамические системы с приложениями с использованием Maple 2-е изд.. Springer. ISBN 978-0-8176-4389-8.
Стивен Линч (2014). Динамические системы с приложениями, использующими MATLAB 2nd Edition. Издательство Springer International. ISBN 978-3319068190.
Стивен Линч (2017). Динамические системы с приложениями с использованием Mathematica 2-е изд.. Springer. ISBN 978-3-319-61485-4.
Стивен Линч (2018). Динамические системы с приложениями, использующими Python. Издательство Springer International. ISBN 978-3-319-78145-7.
Джеймс Мейсс (2007). Дифференциальные динамические системы. СИАМ. ISBN 978-0-89871-635-1.
Дэвид Д. Нолти (2015). Введение в современную динамику: хаос, сети, пространство и время. Издательство Оксфордского университета. ISBN 978-0199657032.
Жюльен Клинтон Спротт (2003). Хаос и анализ временных рядов. Издательство Оксфордского университета. ISBN 978-0-19-850839-7.
Стивен Х. Строгац (1994). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике. Эддисон Уэсли. ISBN 978-0-201-54344-5.
Тешл, Джеральд (2012). Обыкновенные дифференциальные уравнения и динамические системы.. Провиденс: Американское математическое общество. ISBN 978-0-8218-8328-0.
Стивен Виггинс (2003). Введение в прикладные динамические системы и хаос. Springer. ISBN 978-0-387-00177-7.

Популяризации:

Флорин Дьяку и Филип Холмс (1996). Небесные встречи. Принстон. ISBN 978-0-691-02743-2.
Джеймс Глейк (1988). Хаос: создание новой науки. Пингвин. ISBN 978-0-14-009250-9.
Ивар Экеланд (1990). Математика и неожиданное (мягкая обложка). Издательство Чикагского университета. ISBN 978-0-226-19990-0.
Ян Стюарт (1997). Играет ли Бог в кости? Новая математика хаоса. Пингвин. ISBN 978-0-14-025602-4.

внешняя ссылка

Сервер препринтов Arxiv имеет ежедневное представление (нерецензированных) рукописей в динамических системах.
Энциклопедия динамических систем Часть Scholarpedia - рецензируются и написаны приглашенными экспертами.
Нелинейная динамика. Модели бифуркации и хаоса Элмера Г. Винса
Sci.Nonlinear FAQ 2.0 (сентябрь 2003 г.) предоставляет определения, объяснения и ресурсы, связанные с нелинейной наукой

Интернет-книги или конспекты лекций

Геометрическая теория динамических систем. Конспект лекций Нильса Берглунда для курса в ETH на продвинутом уровне бакалавриата.
Динамические системы. В книге Джорджа Д. Биркгофа 1927 года уже используется современный подход к динамическим системам.
Хаос: классический и квантовый. Введение в динамические системы с точки зрения периодической орбиты.
Обучающие динамические системы. Учебник по изучению динамических систем.
Обыкновенные дифференциальные уравнения и динамические системы.. Конспект лекций Джеральд Тешл

Исследовательские группы

Группа Динамических Систем Гронинген, IWI, Университет Гронингена.
Хаос @ UMD. Концентрируется на приложениях динамических систем.
[1], СУНИ Стоуни Брук. Списки конференций, исследователей и некоторые открытые проблемы.
Центр динамики и геометрии, Штат Пенсильвания.
Системы управления и динамические системы, Калтех.
Лаборатория нелинейных систем, Федеральная политехническая школа Лозанны (EPFL).
Центр динамических систем, Бременский университет
Группа системного анализа, моделирования и прогнозирования, Оксфордский университет
Группа нелинейной динамики, Instituto Superior Técnico, Технический университет Лиссабона
Динамические системы, IMPA, Instituto Nacional de Matemática Pura e Applicada.
Рабочая группа по нелинейной динамике, Институт компьютерных наук Чешской академии наук.
UPC Dynamical Systems Group, Барселона, Политехнический университет Каталонии.
Центр управления, динамических систем и вычислений, Калифорнийский университет в Санта-Барбаре.

[1] Строгац, С. Х. (2001). Нелинейная динамика и хаос: с приложениями к физике, биологии и химии. Персей.

[2] Каток, А .; Хассельблатт, Б. (1995). Введение в современную теорию динамических систем. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-34187-5.

[3] "Природа". Springer Nature. Получено 17 февраля 2017.

[4] Melby, P .; и другие. (2005). «Динамика самонастраивающихся систем с шумом». Хаос: междисциплинарный журнал нелинейной науки. 15 (3): 033902. Bibcode:2005 Хаос..15c3902M. Дои:10.1063/1.1953147. PMID 16252993.

[5] Гинтаутас, В .; и другие. (2008). «Резонансное форсирование выбранных степеней свободы многомерной хаотической динамики карты». J. Stat. Phys. 130. arXiv:0705.0311. Bibcode:2008JSP ... 130..617G. Дои:10.1007 / s10955-007-9444-4. S2CID 8677631.

[6] Джексон, Т .; Радунская, А. (2015). Применение динамических систем в биологии и медицине. Springer.

[7] Крейсциг, Эрвин (2011). Высшая инженерная математика. Хобокен: Вайли. ISBN 978-0-470-64613-7.

[8] Гандольфо, Джанкарло (2009) [1971]. Экономическая динамика: методы и модели (Четвертое изд.). Берлин: Springer. ISBN 978-3-642-13503-3.

[9] Холмс, Филип. «Пуанкаре, небесная механика, теория динамических систем и« хаос »». Отчеты по физике 193.3 (1990): 137-163.

[Rega-10] Рега, Джузеппе (2019). «Дань Али Х. Найфе (1933-2017)». Симпозиум IUTAM по использованию нелинейной динамики для инженерных систем. Springer. С. 1–2. ISBN 9783030236922.

[fi-11] «Али Хасан Найфех». Награды института Франклина. Институт Франклина. 4 февраля 2014 г.. Получено 25 августа 2019.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]