Аттрактор Рёсслера - Rössler attractor

Аттрактор Рёсслера

Аттрактор Рёсслера как стереограмма с участием ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, ${\displaystyle c=14}$

В Аттрактор Рёсслера /ˈрɒsлər/ это аттрактор для Система Рёсслера, система трех нелинейный обыкновенные дифференциальные уравнения первоначально изученный Отто Рёсслер.^[1][2] Эти дифференциальные уравнения определяют динамическая система с непрерывным временем что показывает хаотичный динамика, связанная с фрактал свойства аттрактора.^[3]

Некоторые свойства системы Рёсслера можно вывести с помощью линейных методов, таких как собственные векторы, но основные функции системы требуют нелинейных методов, таких как Карты Пуанкаре и бифуркационные диаграммы. В оригинальной статье Рёсслера утверждается, что аттрактор Рёсслера должен вести себя аналогично аттрактору Рёсслера. Аттрактор Лоренца, но также будет легче анализировать качественно.^[1] An орбита внутри аттрактора следует по внешней спирали, близкой к ${\displaystyle x,y}$ самолет вокруг неустойчивой фиксированной точки. Как только график достаточно развернется по спирали, вторая фиксированная точка влияет на график, вызывая подъем и скручивание ${\displaystyle z}$-размер. Во временной области становится очевидным, что, хотя каждая переменная колеблется в пределах фиксированного диапазона значений, колебания являются хаотическими. Этот аттрактор имеет некоторое сходство с аттрактором Лоренца, но он проще и имеет только один многообразие. Отто Рёсслер разработал аттрактор Рёсслера в 1976 г.,^[1] но первоначально теоретические уравнения позже оказались полезными при моделировании равновесия в химических реакциях.

Определение

Определяющими уравнениями системы Рёсслера являются:^[3]

${\displaystyle {\begin{cases}{\frac {dx}{dt}}=-y-z\\{\frac {dy}{dt}}=x+ay\\{\frac {dz}{dt}}=b+z(x-c)\end{cases}}}$

Рёсслер изучил хаотический аттрактор с участием ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, и ${\displaystyle c=5.7}$, хотя свойства ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, и ${\displaystyle c=14}$ с тех пор стали использоваться чаще. Другая линия пространства параметров была исследована с помощью топологического анализа. Это соответствует ${\displaystyle b=2}$, ${\displaystyle c=4}$, и ${\displaystyle a}$ был выбран в качестве параметра бифуркации.^[4] Как Рёсслер открыл эту систему уравнений, исследовали Летелье и Мессагер.^[5]

Анализ

${\displaystyle x,y}$ плоскости аттрактора Рёсслера с ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, ${\displaystyle c=5.7}$

Отчасти элегантность аттрактора Рёсслера объясняется тем, что два его уравнения линейны; установка ${\displaystyle z=0}$, позволяет исследовать поведение на ${\displaystyle x,y}$ самолет

${\displaystyle {\begin{cases}{\frac {dx}{dt}}=-y\\{\frac {dy}{dt}}=x+ay\end{cases}}}$

Стабильность в ${\displaystyle x,y}$ плоскость затем можно найти, вычислив собственные значения из Якобиан ${\displaystyle {\begin{pmatrix}0&-1\\1&a\\\end{pmatrix}}}$, которые ${\displaystyle (a\pm {\sqrt {a^{2}-4}})/2}$. Из этого мы видим, что когда ${\displaystyle 0<a<2}$, собственные значения являются комплексными, и оба имеют положительную действительную составляющую, что делает начало координат нестабильным из-за внешней спирали на ${\displaystyle x,y}$ самолет. Теперь рассмотрим ${\displaystyle z}$ плоское поведение в контексте этого диапазона для ${\displaystyle a}$. Пока ${\displaystyle x}$ меньше чем ${\displaystyle c}$, то ${\displaystyle c}$ срок будет держать орбиту близко к ${\displaystyle x,y}$ самолет. По мере приближения орбиты ${\displaystyle x}$ лучше чем ${\displaystyle c}$, то ${\displaystyle z}$-значения начинают расти. Так как ${\displaystyle z}$ поднимается, однако, ${\displaystyle -z}$ в уравнении для ${\displaystyle dx/dt}$ останавливает рост ${\displaystyle x}$.

Фиксированные точки

Чтобы найти неподвижные точки, три уравнения Рёсслера устанавливаются равными нулю и (${\displaystyle x}$,${\displaystyle y}$,${\displaystyle z}$) координаты каждой фиксированной точки определялись путем решения полученных уравнений. Это дает общие уравнения каждой из координат неподвижной точки ^[6]:

${\displaystyle {\begin{cases}x={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2}}\\y=-\left({\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\right)\\z={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\end{cases}}}$

Что, в свою очередь, можно использовать для отображения фактических фиксированных точек для данного набора значений параметров:

${\displaystyle \left({\frac {c+{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c-{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c+{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

${\displaystyle \left({\frac {c-{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c+{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c-{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

Как показано на общих графиках аттрактора Ресслера выше, одна из этих неподвижных точек находится в центре петли аттрактора, а другая - относительно далеко от аттрактора.

Собственные значения и собственные векторы

Устойчивость каждой из этих фиксированных точек можно проанализировать, определив их соответствующие собственные значения и собственные векторы. Начиная с якобиана:

${\displaystyle {\begin{pmatrix}0&-1&-1\\1&a&0\\z&0&x-c\\\end{pmatrix}}}$

собственные значения можно определить, решив следующую кубику:

${\displaystyle -\lambda ^{3}+\lambda ^{2}(a+x-c)+\lambda (ac-ax-1-z)+x-c+az=0\,}$

Для центральной фиксированной точки исходные значения параметров Ресслера a = 0,2, b = 0,2 и c = 5,7 дают собственные значения:

${\displaystyle \lambda _{1}=0.0971028+0.995786i\,}$

${\displaystyle \lambda _{2}=0.0971028-0.995786i\,}$

${\displaystyle \lambda _{3}=-5.68718\,}$

Величина отрицательного собственного значения характеризует уровень притяжения вдоль соответствующего собственного вектора. Точно так же величина положительного собственного значения характеризует уровень отталкивания по соответствующему собственному вектору.

Собственные векторы, соответствующие этим собственным значениям:

${\displaystyle v_{1}={\begin{pmatrix}0.7073\\-0.07278-0.7032i\\0.0042-0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.7073\\0.07278+0.7032i\\0.0042+0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.1682\\-0.0286\\0.9853\\\end{pmatrix}}}$

Исследование собственных векторов центральной неподвижной точки: синяя линия соответствует стандартному аттрактору Ресслера, генерируемому с помощью ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, и ${\displaystyle c=5.7}$.

Аттрактор Рёсслера с ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, ${\displaystyle c=5.7}$

Эти собственные векторы имеют несколько интересных следствий. Во-первых, две пары собственное значение / собственный вектор (${\displaystyle v_{1}}$ и ${\displaystyle v_{2}}$) ответственны за устойчивое скольжение наружу, которое происходит в основном диске аттрактора. Последняя пара собственное значение / собственный вектор притягивает вдоль оси, которая проходит через центр многообразия и учитывает движение по оси z, которое происходит внутри аттрактора. Этот эффект примерно демонстрируется на рисунке ниже.

На рисунке исследуются собственные векторы центральной неподвижной точки. Синяя линия соответствует стандартному аттрактору Рёсслера, генерируемому с помощью ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, и ${\displaystyle c=5.7}$. Красная точка в центре этого аттрактора - это ${\displaystyle FP_{1}}$. Красная линия, пересекающая эту фиксированную точку, является иллюстрацией плоскости отталкивания, создаваемой ${\displaystyle v_{1}}$ и ${\displaystyle v_{2}}$. Зеленая линия - это иллюстрация привлекающего ${\displaystyle v_{3}}$. Пурпурная линия образуется путем отступления назад во времени от точки на собственном векторе притяжения, которая немного выше ${\displaystyle FP_{1}}$ - он иллюстрирует поведение точек, над которыми полностью доминирует этот вектор. Обратите внимание, что пурпурная линия почти касается плоскости аттрактора, прежде чем подтянуться вверх в фиксированную точку; это говорит о том, что общий вид и поведение аттрактора Ресслера в значительной степени является продуктом взаимодействия между притягивающими ${\displaystyle v_{3}}$ и отталкивающий ${\displaystyle v_{1}}$ и ${\displaystyle v_{2}}$ самолет. В частности, это означает, что последовательность, сгенерированная из уравнений Рёсслера, начнет циклически повторяться. ${\displaystyle FP_{1}}$, начните тянуть вверх в ${\displaystyle v_{3}}$ вектор, создавая восходящее плечо кривой, которая слегка изгибается внутрь по направлению к вектору, прежде чем снова вытолкнуть наружу, когда он тянется обратно к плоскости отталкивания.

Для фиксированной точки выброса исходные значения параметров Рёсслера ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, и ${\displaystyle c=5.7}$ дают собственные значения:

${\displaystyle \lambda _{1}=-0.0000046+5.4280259i}$

${\displaystyle \lambda _{2}=-0.0000046-5.4280259i}$

${\displaystyle \lambda _{3}=0.1929830}$

Собственные векторы, соответствующие этим собственным значениям:

${\displaystyle v_{1}={\begin{pmatrix}0.0002422+0.1872055i\\0.0344403-0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.0002422-0.1872055i\\0.0344403+0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.0049651\\-0.7075770\\0.7066188\\\end{pmatrix}}}$

Хотя эти собственные значения и собственные векторы существуют в аттракторе Ресслера, их влияние ограничено итерациями системы Ресслера, начальные условия которой находятся в общей окрестности этой фиксированной точки выброса. За исключением тех случаев, когда начальные условия лежат в плоскости притяжения, создаваемой ${\displaystyle \lambda _{1}}$ и ${\displaystyle \lambda _{2}}$, это влияние эффективно включает подталкивание результирующей системы к общему аттрактору Ресслера. Когда результирующая последовательность приближается к центральной неподвижной точке и к самому аттрактору, влияние этой удаленной неподвижной точки (и ее собственных векторов) будет уменьшаться.

Карта Пуанкаре

Отображение Пуанкаре для аттрактора Рёсслера с ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, ${\displaystyle c=14}$

В Карта Пуанкаре строится путем построения графика значения функции каждый раз, когда она проходит через заданную плоскость в определенном направлении. Примером может быть построение ${\displaystyle y,z}$ значение каждый раз, когда он проходит через ${\displaystyle x=0}$ самолет, где ${\displaystyle x}$ меняется с отрицательного на положительный, что обычно делается при изучении аттрактора Лоренца. В случае аттрактора Ресслера ${\displaystyle x=0}$ самолет неинтересен, так как карта всегда пересекает ${\displaystyle x=0}$ самолет в ${\displaystyle z=0}$ из-за природы уравнений Рёсслера. в ${\displaystyle x=0.1}$ самолет для ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, ${\displaystyle c=14}$карта Пуанкаре показывает подъем ${\displaystyle z}$ ценности как ${\displaystyle x}$ увеличивается, как и следовало ожидать из-за подъема и скручивания участка графика Ресслера. Количество точек на этом конкретном графике Пуанкаре бесконечно, но когда ${\displaystyle c}$ значение, количество точек может варьироваться. Например, с ${\displaystyle c}$ значение 4, есть только одна точка на отображении Пуанкаре, потому что функция дает периодическую орбиту периода один, или если ${\displaystyle c}$ установлено значение 12,8, будет шесть точек, соответствующих шестому периоду обращения по орбите.

Отображение локальных максимумов

${\displaystyle Z_{n}}$ vs. ${\displaystyle Z_{n+1}}$

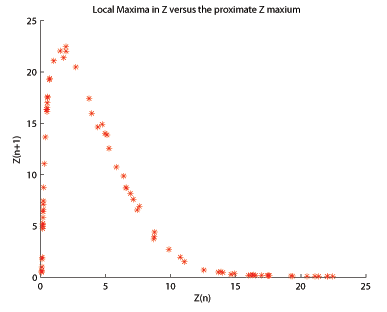
В оригинальной статье об аттракторе Лоренца^[7] Эдвард Лоренц проанализировали локальные максимумы ${\displaystyle z}$ против непосредственно предшествующих локальных максимумов. При визуализации сюжет напоминал карта палатки, подразумевая, что аналогичный анализ может использоваться между картой и аттрактором. Для аттрактора Ресслера, когда ${\displaystyle z_{n}}$ локальный максимум наносится на следующий локальный ${\displaystyle z}$ максимум, ${\displaystyle z_{n+1}}$, итоговый график (показан здесь для ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, ${\displaystyle c=5.7}$) является одномодальным, напоминающим перекошенный Карта Энона. Зная, что аттрактор Рёсслера можно использовать для создания псевдо-одномерного отображения, следует использовать аналогичные методы анализа. Бифуркационная диаграмма - особенно полезный метод анализа.

Вариация параметров

Поведение аттрактора Рёсслера во многом зависит от значений его постоянных параметров. ${\displaystyle a}$, ${\displaystyle b}$, и ${\displaystyle c}$. В общем, изменение каждого параметра имеет сравнимый эффект, заставляя систему сходиться к периодической орбите, фиксированной точке или уходить в бесконечность, однако конкретные диапазоны и индуцированное поведение существенно различаются для каждого параметра. Периодические орбиты или «единичные циклы» системы Рёсслера определяются числом витков вокруг центральной точки, которые возникают до того, как серия петель начинает повторяться.

Бифуркационные диаграммы являются обычным инструментом для анализа поведения динамические системы, одним из которых является аттрактор Рёсслера. Они создаются путем выполнения уравнений системы, сохранения всех переменных, кроме одной, постоянными, и изменения последней. Затем строится график точек, в которых конкретное значение для измененной переменной посещается после нейтрализации переходных факторов. Хаотические области обозначаются закрашенными участками графика.

Варьируя

Вот, ${\displaystyle b}$ фиксируется на 0,2, ${\displaystyle c}$ установлен на 5,7 и ${\displaystyle a}$ изменения. Численное исследование поведения аттрактора при изменении ${\displaystyle a}$ предполагает, что он оказывает непропорциональное влияние на поведение аттрактора. Результаты анализа:

• ${\displaystyle a\leq 0}$: Сходится к центральной фиксированной точке
• ${\displaystyle a=0.1}$: Единичный цикл периода 1
• ${\displaystyle a=0.2}$: Стандартное значение параметра, выбранное Рёсслером, хаотичное.
• ${\displaystyle a=0.3}$: Хаотический аттрактор, значительно больше Лента Мебиуса -подобный (складывающийся).
• ${\displaystyle a=0.35}$: Подобно .3, но все более хаотично
• ${\displaystyle a=0.38}$: Подобно .35, но все более хаотично.

Варьируя b

Бифуркационная диаграмма аттрактора Ресслера при варьировании ${\displaystyle b}$

Вот, ${\displaystyle a}$ фиксируется на 0,2, ${\displaystyle c}$ установлен на 5,7 и ${\displaystyle b}$ изменения. Как показано на прилагаемой диаграмме, как ${\displaystyle b}$ стремится к 0, аттрактор приближается к бесконечности (обратите внимание на подъем для очень малых значений ${\displaystyle b}$. По сравнению с другими параметрами, варьирующимися ${\displaystyle b}$ генерирует больший диапазон при появлении орбит с периодом 3 и периодом 6. В отличие от ${\displaystyle a}$ и ${\displaystyle c}$, более высокие значения ${\displaystyle b}$ сходятся к периоду-1, а не к хаотическому состоянию.

Различный c

Бифуркационная диаграмма аттрактора Ресслера при варьировании ${\displaystyle c}$

Вот, ${\displaystyle a=b=0.1}$ и ${\displaystyle c}$ изменения. В бифуркационная диаграмма показывает, что низкие значения ${\displaystyle c}$ периодические, но быстро становятся хаотическими, поскольку ${\displaystyle c}$ увеличивается. Этот шаблон повторяется как ${\displaystyle c}$ возрастает - есть участки периодичности, чередующиеся с периодами хаоса, и тенденция к орбитам с более высокими периодами, поскольку ${\displaystyle c}$ увеличивается. Например, период один оборот появляется только для значений ${\displaystyle c}$ около 4 и больше не встречается на бифуркационной диаграмме. То же явление наблюдается с периодом три; до тех пор ${\displaystyle c=12}$орбиты периода три могут быть найдены, но после этого они не появляются.

Графическая иллюстрация изменения аттрактора в диапазоне ${\displaystyle c}$ Значения иллюстрируют общее поведение, наблюдаемое для всех этих анализов параметров - частые переходы между периодичностью и апериодичностью.

Различный c

c = 4, период 1

c = 6, период 2

c = 8.5, период 4

c = 8,7, период 8

c = 9, хаотично

c = 12, период 3

c = 12,6, период 6

c = 13, хаотично

c = 18, хаотично

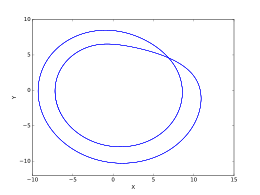
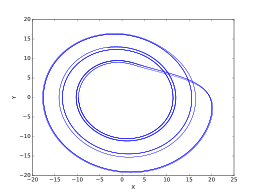
Приведенный выше набор изображений иллюстрирует изменения в пост-переходной системе Рёсслера как ${\displaystyle c}$ варьируется в диапазоне значений. Эти изображения были созданы с помощью ${\displaystyle a=b=.1}$.

• ${\displaystyle c=4}$, орбита периода-1.
• ${\displaystyle c=6}$, орбита периода-2.
• ${\displaystyle c=8.5}$, период-4 орбиты.
• ${\displaystyle c=8.7}$, период 8 орбиты.
• ${\displaystyle c=9}$, разреженный хаотический аттрактор.
• ${\displaystyle c=12}$, орбита периода-3.
• ${\displaystyle c=12.6}$, период-6 орбита.
• ${\displaystyle c=13}$, разреженный хаотический аттрактор.
• ${\displaystyle c=18}$, заполненный хаотический аттрактор.

Периодические орбиты

Аттрактор плотно заполнен периодические орбиты: решения, для которых существует ненулевое значение ${\displaystyle T}$ такой, что ${\displaystyle {\vec {x}}(t+T)={\vec {x}}(t)}$. Эти интересные решения могут быть получены численно, используя Метод Ньютона. Периодические орбиты - это корни функции ${\displaystyle \Phi _{t}-Id}$, где ${\displaystyle \Phi _{t}}$ это эволюция во времени ${\displaystyle t}$ и ${\displaystyle Id}$ это личность. Поскольку большая часть динамики происходит в плоскости x-y, периодические орбиты могут быть классифицированы по их номер намотки вокруг центрального равновесия после проекции.

Таблица периодических орбит по номеру обмотки k

k=1

k = 2

k = 3

Время не в масштабе. Использованы исходные параметры (a, b, c) = (0,2,0,2,5,7).

Из численных экспериментов кажется, что существует уникальная периодическая орбита для всех положительных чисел витков. Это отсутствие вырождения, вероятно, связано с отсутствием симметрии проблемы. Аттрактор можно разбить на более удобные для восприятия инвариантные многообразия: 1D периодические орбиты и 2D устойчивые и неустойчивые многообразия периодических орбит. Эти инвариантные многообразия составляют естественный каркас аттрактора, как и рациональное число относятся к действительные числа.

Для целей теория динамических систем, может быть интересно топологические инварианты этих многообразий. Периодические орбиты являются копиями ${\displaystyle S^{1}}$ встроенный в ${\displaystyle \mathbb {R} ^{3}}$, поэтому их топологические свойства можно понять с помощью теория узлов. Периодические орбиты с номерами витков 1 и 2 образуют Ссылка Хопфа, показывая, что нет диффеоморфизм может разделить эти орбиты.

Ссылки на другие темы

Появление полос в аттракторе Рёсслера похоже на Кантор набор повернулся вокруг своей середины. Кроме того, полувручение, которое происходит в аттракторе Рёсслера, влияет только на его часть. Рёсслер показал, что его аттрактор на самом деле был комбинацией «нормальной полосы» и Лента Мебиуса.^[8]

использованная литература

1. Рёсслер, О. (1976), "Уравнение непрерывного хаоса", Письма по физике, 57A (5): 397–398, Bibcode:1976ФЛА ... 57..397Р, Дои:10.1016/0375-9601(76)90101-8.
2. Рёсслер, О. (1979), «Уравнение гиперхаоса», Письма по физике, 71A (2, 3): 155–157, Bibcode:1979ФЛА ... 71..155Р, Дои:10.1016/0375-9601(79)90150-6.
3. Пайтген, Хайнц-Отто; Юргенс, Хартмут; Саупе, Дитмар (2004), «12.3 Аттрактор Рёсслера», Хаос и фракталы: новые рубежи науки, Springer, стр. 636–646..
4. Letellier, C .; П. Дутертре; Б. Маэ (1995). «Неустойчивые периодические орбиты и шаблоны системы Рёсслера: к систематической топологической характеристике». Хаос. 5 (1): 272–281. Bibcode:1995 Хаос ... 5..271л. Дои:10.1063/1.166076.
5. Letellier, C .; В. Мессагер (2010). «Влияния на самую раннюю работу Отто Э. Рёсслера о хаосе». Международный журнал бифуркации и хаоса. 20 (11): 3585–3616. Bibcode:2010IJBC ... 20.3585L. Дои:10.1142 / s0218127410027854.
6. Martines-Arano, H .; García-Pérez, B.E .; Vidales-Hurtado, M.A .; Trejo-Valdez, M .; Эрнандес-Гомес, L.H .; Торрес-Торрес, К. (2019). «Хаотические сигнатуры, проявляемые плазмонными эффектами в наночастицах Au с клетками». Датчики. 19: 4728.
7. Лоренц, Э. (1963), «Детерминированный непериодический поток», J. Atmos. Sci., 20 (2): 130–141, Bibcode:1963JAtS ... 20..130L, Дои:10.1175 / 1520-0469 (1963) 020 <0130: DNF> 2.0.CO; 2.
8. Рёсслер, Отто Э. (1976). «Хаотическое поведение в простой реакционной системе». Zeitschrift für Naturforschung A. 31 (3–4): 259–264. Bibcode:1976ZNatA..31..259R. Дои:10.1515 / зна-1976-3-408.

внешние ссылки

• Flash-анимация с помощью PovRay
• Rossler1976.pdf
• Аттракторы Лоренца и Рёсслера - Java-анимация
• 3D-аттракторы: программа для Mac для визуализации и исследования аттракторов Ресслера и Лоренца в 3-х измерениях.
• Аттрактор Рёсслера в Scholarpedia
• Аттрактор Рёсслера: численный интерактивный эксперимент в 3D - experience.math.cnrs.fr- (javascript / webgl)