Качающаяся машина Этвуда - Swinging Atwoods machine - Wikipedia
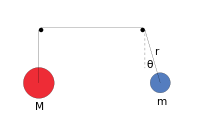
В качающаяся машина Этвуда (SAM) - это механизм, напоминающий простой Машина Этвуда за исключением того, что одна из масс может качаться в двухмерной плоскости, создавая динамическая система то есть хаотичный для некоторых параметров системы и первоначальные условия.
В частности, он состоит из двух масс (маятник, масса и противовес, масса ) связаны нерастяжимый, безмассовая струна подвешена на двух без трения шкивы нулевого радиуса так, чтобы маятник мог свободно вращаться вокруг своего шкива, не сталкиваясь с противовесом.[1]
Обычная машина Этвуда допускает только «побеги» (т.е. либо маятник, либо противовес в конечном итоге сталкивается со своим шкивом), за исключением . Однако качающаяся машина Этвуда с имеет большой пространство параметров условий, которые приводят к множеству движений, которые можно классифицировать как завершающие или не прекращающиеся, периодические, квазипериодические или хаотические, ограниченные или неограниченные, сингулярные или неособые[1][2] из-за маятника реактивная центробежная сила противодействовать весу противовеса.[1] Исследование SAM началось как часть докторской диссертации 1982 г. Улыбки и слезы (имея в виду форму некоторых траекторий системы) на Николас Туфилларо в Рид Колледж, режиссер Дэвид Дж. Гриффитс.[3]
Уравнения движения

Качающаяся машина Этвуда представляет собой систему с двумя степенями свободы. Мы можем вывести его уравнения движения, используя либо Гамильтонова механика или же Лагранжева механика. Пусть качающаяся масса будет а неподвижная масса должна быть . Кинетическая энергия системы, , является:
куда расстояние от качающейся массы до ее оси, а - угол качающейся массы относительно направления прямо вниз. Потенциальная энергия исключительно из-за ускорение силы тяжести:
Затем мы можем записать лагранжиан, , и гамильтониан, системы:
Тогда мы можем выразить гамильтониан через канонические импульсы: , :
Анализ Лагранжа можно применить для получения двух связанных обыкновенных дифференциальных уравнений второго порядка в и . Во-первых, уравнение:
И уравнение:
Упростим уравнения, определив отношение масс . Приведенное выше становится:
Гамильтонов анализ может также применяться для определения четырех ОДУ первого порядка в терминах , и соответствующие им канонические импульсы и :
Обратите внимание, что в обоих этих выводах, если установить и угловая скорость к нулю, полученный частный случай - это регулярное нераскачивающееся Машина Этвуда:
Качающаяся машина Этвуда имеет четырехмерный фазовое пространство определяется , и соответствующие им канонические импульсы и . Однако из-за сохранения энергии фазовое пространство ограничено тремя измерениями.
Система с массивными шкивами
Если шкивы в системе считаются имеющими момент инерции и радиус , тогда гамильтониан SAM равен:[4]
Где Mт эффективная полная масса системы,
Это сводится к версии выше, когда и стать нулевым. Уравнения движения теперь:[4]
куда .
Интегрируемость
Гамильтоновы системы можно классифицировать как интегрируемый и неинтегрируемый. ЗУР интегрируема, когда отношение масс .[5] Система также выглядит вполне нормально для , но случай - единственное известное интегрируемое отношение масс. Было показано, что система не интегрируема при .[6] Для многих других значений отношения масс (и начальных условий) SAM отображает хаотическое движение.
Численные исследования показывают, что когда орбита сингулярна (начальные условия: ) маятник выполняет одиночный симметричный цикл и возвращается в исходное положение, независимо от значения . Когда маленький (почти вертикальный), траектория описывает «слезу», когда она большая, она описывает «сердце». Эти траектории можно точно решить алгебраически, что необычно для системы с нелинейным гамильтонианом.[7]
Траектории
Качающаяся масса качающейся машины Этвуда движется по интересным траекториям или орбитам при различных начальных условиях и различных соотношениях масс. К ним относятся периодические орбиты и орбиты столкновения.
Неособые орбиты
Для определенных условий система выставляет сложное гармоническое движение.[1] Орбита называется невырожденной, если качающаяся масса не касается шкива.
- Выбор неособых орбит

Орбита качающейся машины Атвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Атвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Атвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Атвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.
Периодические орбиты

Когда различные гармонические составляющие в системе находятся в фазе, результирующая траектория является простой и периодической, такой как траектория «улыбки», которая напоминает траекторию обычной маятник, и различные петли.[3][8] Как правило, периодическая орбита существует, когда выполняется следующее:[1]
Простейшим случаем периодических орбит является орбита «улыбки», которую Туфилларо назвал Введите орбиты в своей статье 1984 года.[1]
- Выбор периодических орбит

Орбита "улыбки" качающейся машины Этвуда для , , и нулевая начальная скорость.
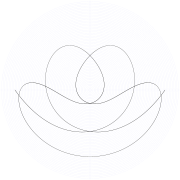
Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.
Особые орбиты
Движение сингулярно, если в какой-то момент качающаяся масса проходит через начало координат. Поскольку система инвариантный при обращении времени и переносе это эквивалентно тому, что маятник начинается в начале координат и запускается наружу:[1]
Область, близкая к оси, особенная, так как близка к нулю и уравнения движения требуют деления на . Поэтому для тщательного анализа этих случаев необходимо использовать специальные методы.[9]
Ниже приведены графики произвольно выбранных особых орбит.
- Выбор особых орбит

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.

Орбита качающейся машины Этвуда для , , и нулевая начальная скорость.
Столкновение орбит
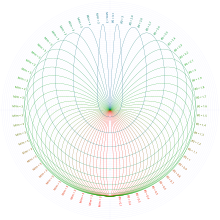
Орбиты столкновения (или завершающие особые) орбиты - это подмножество особых орбит, образующихся, когда качающаяся масса выбрасывается из своей оси с начальной скоростью, так что она возвращается к оси вращения (т. Е. Сталкивается с ней):
Самый простой случай столкновения орбит - орбиты с отношением масс 3, которые всегда будут возвращаться симметрично в исходную точку после выброса из нее, и были названы Тип B орбиты в исходной статье Туфилларо.[1] Их также называли глазницами в форме слезы, сердца или кроличьего уха из-за их внешнего вида.[3][7][8][9]
Когда качающаяся масса возвращается в исходное положение, масса противовеса, должен мгновенно менять направление, вызывая бесконечное натяжение соединительной струны. Таким образом, мы можем считать, что движение прекращается в это время.[1]
Ограниченность
Для любого начального положения можно показать, что качающаяся масса ограничена кривой, которая является коническая секция.[2] Поворот всегда фокус этой ограничивающей кривой. Уравнение для этой кривой может быть получено путем анализа энергии системы и использования сохранения энергии. Предположим, что освобожден от покоя в и . Таким образом, общая энергия системы составляет:
Однако обратите внимание, что в граничном случае скорость качающейся массы равна нулю.[2] Следовательно, мы имеем:
Чтобы увидеть, что это уравнение конического сечения, мы выделяем для :
Обратите внимание, что числитель является константой, зависящей только от начального положения в этом случае, поскольку мы предположили, что начальное состояние находится в состоянии покоя. Однако постоянная энергии также может быть вычислен для ненулевой начальной скорости, и уравнение остается верным во всех случаях.[2] В эксцентриситет конического сечения . За , это эллипс, а система ограничена, и качающаяся масса всегда остается внутри эллипса. За , это парабола и для это гипербола; в любом из этих случаев он не ограничен. В качестве становится сколь угодно большим, ограничивающая кривая приближается к окружности. Область, ограниченная кривой, известна как область Хилла.[2]
Недавнее трехмерное расширение
В 2016 году был анонсирован новый интегрируемый случай проблемы трехмерной вращающейся машины Этвуда (3D-SAM).[10] Как и в 2D-версии, проблема интегрируема, когда .
Рекомендации
- ^ а б c d е ж грамм час я Туфилларо, Николас Б .; Abbott, Tyler A .; Гриффитс, Дэвид Дж. (1984). «Качающаяся машина Этвуда». Американский журнал физики. 52 (10): 895–903. Bibcode:1984AmJPh..52..895T. Дои:10.1119/1.13791.
- ^ а б c d е Туфилларо, Николас Б .; Nunes, A .; Касасаяс, Дж. (1988). «Неограниченные орбиты качающейся машины Этвуда». Американский журнал физики. 56: 1117. Bibcode:1988AmJPh..56.1117T. Дои:10.1119/1.15774.
- ^ а б c Туфилларо, Николас Б. (1982). Улыбки и слезы (Тезис). Рид Колледж.
- ^ а б Пужоль, Оливье; Perez, J.P .; Simo, C .; Саймон, С .; Вейль, Дж. (2010). «Качающаяся машина Этвуда: экспериментальные и численные результаты, а также теоретическое исследование». Physica D. 239 (12): 1067–1081. arXiv:0912.5168. Bibcode:2010PhyD..239.1067P. Дои:10.1016 / j.physd.2010.02.017.
- ^ Туфилларо, Николас Б. (1986). «Интегрируемое движение качающейся машины Этвуда». Американский журнал физики. 54 (2): 142. Bibcode:1986AmJPh..54..142T. Дои:10.1119/1.14710.
- ^ Casasayas, J .; Nunes, A .; Туфилларо, Н. (1990). «Качающаяся машина Этвуда: интегрируемость и динамика». Journal de Physique. 51 (16): 1693–1702. Дои:10.1051 / jphys: 0199000510160169300. ISSN 0302-0738.
- ^ а б Туфилларо, Николас Б. (1994). "Слеза и сердечные орбиты качающейся машины Этвудса". Американский журнал физики. 62 (3): 231–233. arXiv:chao-dyn / 9302006. Bibcode:1994AmJPh..62..231T. Дои:10.1119/1.17602.
- ^ а б Туфилларо, Николас Б. (1985). «Движения качающейся машины Этвуда». Journal de Physique. 46 (9): 1495–1500. Дои:10.1051 / jphys: 019850046090149500.
- ^ а б Туфилларо, Николас Б. (1985). «Столкновение орбит качающейся машины Этвуда» (PDF). Journal de Physique. 46: 2053–2056. Дои:10.1051 / jphys: 0198500460120205300.
- ^ Эльмандух, А.А. (2016). «Об интегрируемости движения трехмерного качающегося станка Этвуда и связанных с этим проблем». Письма о физике A. 380: 989. Bibcode:2016ФЛА..380..989Е. Дои:10.1016 / j.physleta.2016.01.021.
дальнейшее чтение
- Алмейда, М.А., Морейра, И.С. и Santos, F.C. (1998) "Об анализе Зиглина-Йошиды для некоторых классов однородных гамильтоновых систем", Бразильский журнал физики Том 28, номер 4, Сан-Паулу, декабрь.
- Баррера, Эммануэль Ян (2003) Динамика двухкачажной машины Этвуда, Б.С. Диссертация, Национальный институт физики, Филиппинский университет.
- Бабелон, О., М. Талон, М.К. Пейранере (2010), «Анализ Ковалевски качающейся машины Этвуда», Журнал физики A: математический и теоретический Vol. 43 (8).
- Брун Б. (1987) "Хаос и порядок в слабосвязанных системах нелинейных осцилляторов". Physica Scripta Том 35 (1).
- Дж. Касасаяс, Н. Б. Туфилларо и А. Нунес (1989) "Бесконечное многообразие качающейся машины Этвуда". Европейский журнал физики Том 10 (10), с. 173.
- Касасаяс, Дж., А. Нуньес и Н. Б. Туфилларо (1990) «Качающаяся машина Этвуда: интегрируемость и динамика». Journal de Physique Том 51, стр. 1693.
- Чоудхури, А. Рой и М. Дебнат (1988) "Качающаяся машина Этвуда. Дальняя и близкая к резонансной области", Международный журнал теоретической физики, Vol. 27 (11), с. 1405-1410.
- Гриффитс Д. Дж. И Т. А. Эбботт (1992) "Комментарий к" "Удивительная демонстрация механики" " Американский журнал физики Том 60 (10), с. 951-953.
- Морейра, И. и М.А. Алмейда (1991) «Симметрии Нётер и качающаяся машина Этвуда», Журнал физики II Франция 1, стр. 711-715.
- А. Нунес, Дж. Касасаяс и Н. Б. Туфилларо (1995) "Периодические орбиты интегрируемой качающейся машины Атвуда". Американский журнал физики Том 63 (2), с. 121-126.
- Ouazzani-T.H., A. и Ouzzani-Jamil, M., (1995) "Бифуркации торов Лиувилля интегрируемого случая качающейся машины Атвуда". Il Nuovo Cimento B Vol. 110 (9).
- Оливье, Пуйоль, JP Perez, JP Ramis, C. Simo, S. Simon, JA Weil (2010), «Качающаяся машина Этвуда: экспериментальные и численные результаты, а также теоретическое исследование». Physica D 239. С. 1067–1081.
- Sears, R. (1995) "Комментарий к" Удивительной демонстрации механики ", Американский журнал физики, Vol. 63 (9), с. 854-855.
- Йехиа, Х.М., (2006) "Об интегрируемости движения тяжелой частицы на наклонном конусе и качающейся машине Атвуда", Сообщения об исследованиях в области механики Vol. 33 (5), стр. 711–716.
внешняя ссылка
- Пример использования в бакалавриате: симплектические интеграторы
- Курс Имперского колледжа
- Oscilaciones en la máquina de Atwood
- «Улыбки и слезы» (1982)
- 2007 Мастерская
- 2010 Видео экспериментальной качающейся машины Этвуда
- Обновленная информация о качающейся машине Этвуда на заседании APS 2010 г., 8:24, пятница, 19 марта 2010 г., Портленд, Орегон
- Интерактивное веб-приложение Swinging Atwood's Machine
- Открытый исходный код Java для запуска Swinging Atwood's Machine
















































































