Внешний бильярд - Outer billiard

Внешний бильярд это динамическая система на основе выпуклый форма в плоскости. Классически эта система определяется для Евклидова плоскость но можно также рассмотреть систему в гиперболическая плоскость или в других пространствах, подходящих для обобщения плоскости. Внешний бильярд отличается от обычного динамический бильярд в том, что он имеет дело с дискретной последовательностью ходов за пределами форма, а не внутри нее.

Определения

Внешняя карта бильярда

Пусть P будет выпуклый Если задана точка x0 вне P, обычно существует уникальная точка x1 (также вне P), так что отрезок линии, соединяющий x0 с x1, равен касательная к P на его середина и человек, идущий от x0 к x1, увидит P справа. (См. Рисунок.) MapF: x0 -> x1 называется внешняя карта бильярда.

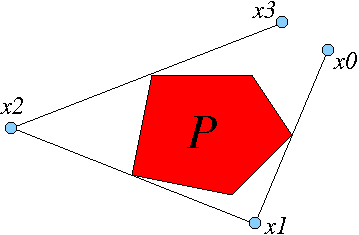
Внешний бильярд определяется относительно пятиугольника

В обратный (или наоборот) внешнее отображение биллиарда также определяется как отображение x1 -> x0. Обратную карту можно получить, просто заменив слово верно к слову оставили в приведенном выше определении. Рисунок показывает ситуацию в Евклидова плоскость, но определение вгиперболическая плоскость по сути то же самое.

Орбиты

Внешний бильярд орбита это набор всех итерации точки, а именно ... x0 <--> x1 <--> x2 <--> x3 ... То есть, начните с x0 и итеративно примените как внешнее отображение биллиарда, так и обратное внешнее отображение биллиарда. строго выпуклая форма, например эллипс, каждая точка вне P имеет корректно определенную орбиту. Когда писа многоугольник, некоторые точки могут не иметь четко определенных орбит из-за потенциальной неоднозначности выбора средней точки соответствующей касательной. Тем не менее в многоугольном случае почти каждый точка имеет четко определенную орбиту.

Орбита называется периодический если это в конечном итоге повторится.
Орбита называется апериодический (или же непериодический), если он не периодический.
Орбита называется ограниченный (или же стабильный), если некоторая ограниченная область на плоскости содержит всю орбиту.
Орбита называется неограниченный (или же неустойчивый), если он не ограничен.

Многомерные пространства

Определение внешней биллиардной системы в многомерном пространстве выходит за рамки данной статьи. В отличие от обычного бильярд, определение не однозначно. Естественным местом для карты является комплексное векторное пространство. В этом случае есть естественный выбор прямой, касательной к выпуклый тело в каждой точке. Эти касательные можно получить, начав с нормалей и используя сложная структура повернуть на 90 градусов. Эти выделенные касательные можно использовать для определения внешнего биллиарда примерно так, как указано выше. Подробнее см. Книгу С. Табачникова (цитируется в ссылках).

История

Большинство людей приписывают появление внешнего бильярда Бернхард Нойманн в конце 1950-х, хотя кажется, что некоторые люди ссылаются на более раннюю постройку 1945 года, построенную М. Дэем. Юрген Мозер популяризировал систему в 1970-х как игрушечную модель длянебесная механика. Эта система изучалась классически в Евклидова плоскость, а совсем недавно в гиперболическая плоскость. Можно также рассматривать многомерные пространства, хотя серьезных исследований еще не проводилось.Бернхард Нойманн неформально поставил вопрос о том, можно ли иметь неограниченные орбиты во внешней бильярдной системе, и Мозер сформулировал его в письменной форме в 1973 г. Иногда этот основной вопрос называли вопрос Мозера-Неймана.Этот вопрос изначально задавался для фигур в Евклидова плоскость и решенная только недавно, возникла серьезная проблема в этой области.

Вопрос Мозера-Неймана

Ограниченные орбиты на евклидовой плоскости

В 70-е годы Юрген Мозер набросал доказательство, основанное на К.А.М. теория, что внешний биллиард относительно a6-кратнодифференцируемый форма позитивного кривизна ограничены все орбиты. В 1982 г. Рафаэль Дуади дало полное доказательство этого результата. Большой прогресс в многоугольном случае произошел в течение нескольких лет, когда три авторских коллектива, Вивальди-Шайденко (1987), Колодзей (1989) и Гуткин-Симаньи (1991), использовали разные методы, показали, что внешний бильярд относительно квазирациональный У многоугольника все орбиты ограничены. Понятие квазирациональности носит технический характер (см. Ссылки), но включает в себя класс правильные многоугольники и выпуклые рациональные многоугольники, а именно те выпуклые многоугольники чьи вершины имеют рациональный координаты. В случае рациональных многоугольников все орбиты периодичны. В 1995 году Табачников показал, что внешний бильярд для правильный пятиугольник имеет некоторые апериодические орбиты, тем самым проясняя различие между динамикой в рациональном и регулярном случаях. В 1996 г. Бойленд показал, что внешние биллиарды относительно некоторых фигур могут иметь орбиты, которые накапливаются в форме. В 2005 г. Д. Генин показал, что все орбиты являются ограничен, когда форма является трапеция, тем самым показывая, что квазирациональность не необходимо условие ограниченности всех орбит системы (не все трапеции квазирациональны.)

Неограниченные орбиты на евклидовой плоскости

В 2007 году Р. Э. Шварц показал, что у внешнего бильярда есть неограниченные орбиты, если их определить относительно Пенроуз Воздушный змей, таким образом отвечая на исходный вопрос Мозера-Неймана утвердительно. выпуклый четырехугольник от воздушных змеев и дротиков Мозаики Пенроуза Впоследствии Шварц показал, что внешний бильярд имеет неограниченные орбиты, когда он определяется относительно любого иррационального воздушного змея. Anиррациональный змей это четырехугольник со следующим свойством: Один из диагонали из четырехугольник делит регион на два треугольники равной площади и другой диагональ делит регион на два треугольники чьи районы не рациональный В 2008 году Долгопят-Фаяд показал, что внешние биллиарды, определенные относительно полудиска, имеют неограниченные орбиты. В полудиск это область, которую можно получить, разрезая диск Доказательство Долгопят-Фаяда надежно и также работает для областей, полученных путем разрезания диска почти пополам, когда слово Около правильно интерпретируется.

Неограниченные орбиты в гиперболической плоскости

В 2003 году Догру и Табачников показали, что все орбиты неограниченны для определенного класса выпуклые многоугольники в гиперболическая плоскость Такие полигоны авторы называют большой. (См. Ссылку для определения.) Затем Догру и Оттен расширили эту работу в 2011 году, указав условия, при которых у правильной многоугольной таблицы в гиперболической плоскости все орбиты неограничены, то есть являются большими.

Существование периодических орбит

В обычном многоугольный бильярд, существование периодических орбит - большая нерешенная проблема. Например, неизвестно, есть ли у каждого стола треугольной формы периодическая биллиардная дорожка. Больший прогресс был достигнут в отношении внешних биллиардов, хотя ситуация еще далека от понимания. Как упоминалось выше, все орбиты являются периодическими, когда система определена относительно выпуклого рационального многоугольника в Евклидова плоскость. Более того, это старая теорема Ч. Культера (написанная С. Табачниковым) о том, что внешний бильярд относительно любого выпуклый многоугольник имеет периодические орбиты - фактически апериодическую орбиту вне любой данной ограниченной области.

Открытые вопросы

Внешний бильярд все еще находится на начальной стадии. Большинство проблем до сих пор не решены. Вот несколько открытых проблем в этой области.

Покажите, что внешний биллиард относительно почти каждый выпуклый многоугольник имеет неограниченные орбиты.
Покажите, что внешний биллиард относительно правильный многоугольник имеет почти каждый орбита периодическая. Случаи равноматериального треугольника и квадрата тривиальны, и Табачников ответил на это для правильного пятиугольника. Это единственные известные случаи.
шире, охарактеризовать структуру множества периодических орбит относительно типичных выпуклый многоугольник.
понять структуру периодических орбит относительно простых форм в гиперболической плоскости, таких как маленькие равносторонние треугольники.