Гидравлическая механика - Fluid mechanics

Гидравлическая механика это филиал физика озабочен механикой жидкости (жидкости, газы, и плазма ) и силы на них.^[1]:3Он имеет приложения в широком спектре дисциплин, в том числе механический, гражданский, химический и биомедицинская инженерия, геофизика, океанография, метеорология, астрофизика, и биология.

Его можно разделить на статика жидкости, исследование жидкостей в состоянии покоя; и динамика жидкостей, исследование влияния сил на движение жидкости.^[1]:3Это филиал механика сплошной среды, предмет, который моделирует материю без использования информации о том, что она состоит из атомов; то есть моделирует материю из макроскопический точка зрения, а не с микроскопический. Гидромеханика, особенно гидродинамика, является активной областью исследований, как правило, математически сложной. Многие проблемы частично или полностью не решены, и их лучше всего решать численные методы, как правило, с помощью компьютеров. Современная дисциплина, называемая вычислительная гидродинамика (CFD), посвящена этому подходу.^[2] Велосиметрия изображения частиц, экспериментальный метод для визуализации и анализа потока жидкости, также использует преимущества очень визуальной природы потока жидкости.

Краткая история

Основная статья: История гидромеханики

Изучение механики жидкости восходит, по крайней мере, к временам древняя Греция, когда Архимед исследовал статику жидкости и плавучесть и сформулировал свой знаменитый закон, известный теперь как Принцип архимеда, который был опубликован в его работе О плавающих телах - вообще считается первой крупной работой по механике жидкости. Быстрый прогресс в механике жидкости начался с Леонардо да Винчи (наблюдения и эксперименты), Евангелиста Торричелли (изобрел барометр ), Исаак Ньютон (исследовано вязкость ) и Блез Паскаль (исследовано гидростатика, сформулированный Закон Паскаля ), и был продолжен Даниэль Бернулли с введением математической гидродинамики в Гидродинамика (1739).

Невязкое течение было дополнительно проанализировано различными математиками (Жан ле Ронд д'Аламбер, Жозеф Луи Лагранж, Пьер-Симон Лаплас, Симеон Дени Пуассон ) и вязкое течение исследовалось множеством инженеры включая Жан Леонар Мари Пуазей и Готхильф Хаген. Дальнейшее математическое обоснование было предоставлено Клод-Луи Навье и Джордж Габриэль Стоукс в Уравнения Навье – Стокса, и пограничные слои были исследованы (Людвиг Прандтль, Теодор фон Карман ), в то время как различные ученые, такие как Осборн Рейнольдс, Андрей Колмогоров, и Джеффри Ингрэм Тейлор улучшил понимание вязкости жидкости и турбулентность.

Основные филиалы

Статика жидкости

Основная статья: Статика жидкости

Статика жидкости или же гидростатика это раздел механики жидкости, изучающий жидкости на отдыхе. Он включает изучение условий, при которых жидкости находятся в состоянии покоя в стабильный равновесие; и контрастирует с динамика жидкостей, исследование жидкостей в движении. Гидростатика предлагает физические объяснения многих явлений повседневной жизни, например, почему атмосферное давление меняется с высота, почему дерево и масло плавают на воде и почему поверхность воды всегда ровная, независимо от формы емкости. Гидростатика - основа гидравлика, то инженерное дело оборудования для хранения, транспортировки и использования жидкостей. Это также актуально для некоторых аспектов геофизика и астрофизика (например, в понимании тектоника плит и аномалии в Гравитационное поле Земли ), к метеорология, к лекарство (в контексте артериальное давление ) и многие другие области.

Динамика жидкостей

Основная статья: Динамика жидкостей

Динамика жидкостей это подраздел механики жидкости, который занимается поток жидкости- наука о движении жидкостей и газов.^[3] Гидродинамика предлагает систематическую структуру, которая лежит в основе практические дисциплины - который охватывает эмпирические и полуэмпирические законы, вытекающие из измерение расхода и используется для решения практических задач. Решение задачи гидродинамики обычно включает расчет различных свойств жидкости, таких как скорость, давление, плотность, и температура, как функции пространства и времени. В нем есть несколько субдисциплин, в том числе аэродинамика^[4][5][6][7] (исследование воздуха и других газов в движении) и гидродинамика^[8][9] (исследование жидкости в движении). Гидродинамика имеет широкий спектр приложений, включая расчет силы и движения на самолет, определяя массовый расход из нефть через трубопроводы, прогнозируя развитие Погода шаблоны, понимание туманности в межзвездное пространство и моделирование взрывы. Некоторые гидродинамические принципы используются в транспортная инженерия и динамика толпы.

Связь с механикой сплошной среды

Гидравлическая механика - это одна из дисциплин механика сплошной среды, как показано в следующей таблице.

Механика сплошной среды Изучение физики сплошных материалов	Механика твердого тела Изучение физики сплошных материалов с заданной формой покоя.	Эластичность Описывает материалы, которые после нанесения возвращаются в исходную форму. подчеркивает удалены.
		Пластичность Описывает материалы, которые необратимо деформируются после значительного приложенного напряжения.	Реология Изучение материалов как с твердыми, так и с жидкостными характеристиками.
	Гидравлическая механика Изучение физики сплошных материалов, которые деформируются под действием силы.	Неньютоновские жидкости не претерпевают деформаций, пропорциональных приложенному напряжению сдвига.
		Ньютоновские жидкости претерпевают деформации, пропорциональные приложенному напряжению сдвига.

С механической точки зрения жидкость - это вещество, которое не поддерживает напряжение сдвига; поэтому покоящаяся жидкость имеет форму сосуда, в котором она находится. Жидкость в состоянии покоя не имеет напряжения сдвига.

Предположения

Баланс для некоторого интегрированного количества жидкости в контрольный объем заключен в поверхность управления.

Допущения, присущие жидкостной механической обработке физической системы, могут быть выражены с помощью математических уравнений. По сути, предполагается, что каждая жидкостная механическая система подчиняется:

• Сохранение массы
• Сохранение энергии
• Сохранение импульса
• Предположение о континууме

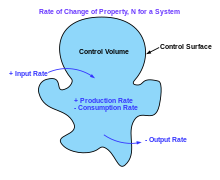
Например, предположение о сохранении массы означает, что для любого фиксированного контрольный объем (например, сферический объем) - окруженный поверхность управления - скорость изменения массы, содержащейся в этом объеме, равна скорости, с которой масса проходит через поверхность от за пределами к внутри, минус скорость, с которой масса проходит от внутри к за пределами. Это можно выразить как уравнение в интегральной форме над контрольным объемом.^[10]:74

В предположение континуума идеализация механика сплошной среды под которыми жидкости можно рассматривать как непрерывный хотя в микроскопическом масштабе они состоят из молекулы. В предположении континуума макроскопические (наблюдаемые / измеряемые) свойства, такие как плотность, давление, температура и объемная скорость, считаются хорошо определенными для «бесконечно малых» элементов объема - малых по сравнению с характерным масштабом длины системы, но большой по сравнению с масштабом молекулярной длины. Свойства жидкости могут непрерывно изменяться от одного элемента объема к другому и представляют собой средние значения молекулярных свойств. Гипотеза континуума может привести к неточным результатам в таких приложениях, как сверхзвуковые скоростные потоки или молекулярные потоки в наномасштабе.^[11] Те проблемы, для которых гипотеза континуума не работает, могут быть решены с использованием статистическая механика. Чтобы определить, применима или нет гипотеза континуума, Число Кнудсена, определяемый как отношение молекулярных длина свободного пробега до характерной длины шкала, оценивается. Проблемы с числами Кнудсена ниже 0,1 можно оценить с помощью гипотезы континуума, но можно применить молекулярный подход (статистическая механика), чтобы найти движение жидкости для больших чисел Кнудсена.

Уравнения Навье – Стокса

Основная статья: Уравнения Навье – Стокса

В Уравнения Навье – Стокса (названный в честь Клод-Луи Навье и Джордж Габриэль Стоукс ) находятся дифференциальные уравнения которые описывают баланс сил в данной точке жидкости. Для несжимаемая жидкость с векторным полем скорости ${\displaystyle \mathbf {u} }$, уравнения Навье – Стокса имеют вид^{[12][13][14][15]}

${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} =-{\frac {1}{\rho }}\nabla P+\nu \nabla ^{2}\mathbf {u} }$.

Эти дифференциальные уравнения для деформируемых материалов являются аналогами уравнений движения Ньютона для частиц - уравнения Навье – Стокса описывают изменения в импульс (сила ) в ответ на давление ${\displaystyle P}$ и вязкость, параметризованная кинематическая вязкость ${\displaystyle \nu }$ здесь. Изредка, силы тела, такие как гравитационная сила или сила Лоренца, добавляются к уравнениям.

Решения уравнений Навье – Стокса для данной физической задачи необходимо искать с помощью исчисление. На практике точно таким образом можно решить только самые простые случаи. Эти случаи обычно связаны с нетурбулентным, устойчивым потоком, в котором Число Рейнольдса маленький. В более сложных случаях, особенно связанных с турбулентность В настоящее время решения уравнений Навье – Стокса, таких как глобальные погодные системы, аэродинамика, гидродинамика и многие другие, можно найти только с помощью компьютеров. Эта отрасль науки называется вычислительная гидродинамика.^{[16][17][18][19][20]}

Невязкие и вязкие жидкости

An невязкая жидкость не имеет вязкость, ${\displaystyle \nu =0}$. На практике невязкий поток - это идеализация, облегчающий математическую обработку. На самом деле, чисто невязкие потоки, как известно, реализуются только в случае сверхтекучесть. В противном случае жидкости обычно вязкий, свойство, которое часто является наиболее важным в пограничный слой возле твердой поверхности,^[21] где поток должен совпадать с условие противоскольжения на твердом. В некоторых случаях математику жидкостной механической системы можно рассматривать, предполагая, что жидкость вне пограничных слоев невязкая, а затем соответствие его решение для тонкого ламинарный пограничный слой.

Для потока жидкости через пористую границу скорость жидкости может быть разной между свободной жидкостью и жидкостью в пористой среде (это связано с условием Бивера и Джозефа). Кроме того, это полезно при низких дозвуковой скорости, чтобы предположить, что газ несжимаемый - то есть плотность газа не меняется, даже если скорость и статическое давление изменять.

Ньютоновская и неньютоновская жидкости

А Ньютоновская жидкость (названный в честь Исаак Ньютон ) определяется как жидкость чей напряжение сдвига линейно пропорциональна скорость градиент в направлении перпендикуляр к плоскости сдвига. Это определение означает, что независимо от сил, действующих на жидкость, она продолжает течь. Например, вода - это ньютоновская жидкость, потому что она продолжает проявлять свойства жидкости независимо от того, сколько ее перемешивают или перемешивают. Чуть менее строгое определение: тащить маленького объекта, медленно перемещающегося через жидкость, пропорционально силе, приложенной к объекту. (Сравнивать трение ). Важные жидкости, такие как вода, а также большинство газов, ведут себя - с хорошим приближением - как ньютоновские жидкости при нормальных условиях на Земле.^[10]:145

Напротив, перемешивание неньютоновская жидкость может оставить после себя «дыру». Со временем он будет постепенно заполняться - такое поведение наблюдается в таких материалах, как пудинг, Oobleck, или же песок (хотя песок не совсем жидкость). В качестве альтернативы, перемешивание неньютоновской жидкости может привести к снижению вязкости, поэтому жидкость будет казаться «тоньше» (это видно при отсутствии капель. краски ). Существует много типов неньютоновских жидкостей, поскольку они определяются как нечто, что не подчиняется определенному свойству - например, большинство жидкостей с длинными молекулярными цепями могут реагировать неньютоновским образом.^[10]:145

Уравнения для ньютоновской жидкости.

Основная статья: Ньютоновская жидкость

Константа пропорциональности между тензором вязких напряжений и градиентом скорости известна как вязкость. Простое уравнение для описания поведения несжимаемой ньютоновской жидкости:

${\displaystyle \tau =-\mu {\frac {dv}{dy}}}$

куда

${\displaystyle \tau }$ напряжение сдвига, оказываемое жидкостью ("тащить ")

${\displaystyle \mu }$ вязкость жидкости - константа пропорциональности

${\displaystyle {\frac {dv}{dy}}}$ - градиент скорости, перпендикулярный направлению сдвига.

Для ньютоновской жидкости вязкость по определению зависит только от температура и давление, а не силы, действующие на него. Если жидкость несжимаемый уравнение, определяющее вязкое напряжение (в Декартовы координаты ) является

${\displaystyle \tau _{ij}=\mu \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}\right)}$

куда

${\displaystyle \tau _{ij}}$ напряжение сдвига на ${\displaystyle i^{th}}$ грань жидкого элемента в ${\displaystyle j^{th}}$ направление

${\displaystyle v_{i}}$ - скорость в ${\displaystyle i^{th}}$ направление

${\displaystyle x_{j}}$ это ${\displaystyle j^{th}}$ координата направления.

Если жидкость несжимаема, общий вид вязкого напряжения в ньютоновской жидкости имеет вид

${\displaystyle \tau _{ij}=\mu \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}-{\frac {2}{3}}\delta _{ij}\nabla \cdot \mathbf {v} \right)+\kappa \delta _{ij}\nabla \cdot \mathbf {v} }$

куда ${\displaystyle \kappa }$ - второй коэффициент вязкости (или объемная вязкость). Если жидкость не подчиняется этому соотношению, ее называют неньютоновская жидкость, которых существует несколько типов. Неньютоновские жидкости могут быть пластичными, пластичными по Бингему, псевдопластическими, дилатантными, тиксотропными, реопектическими, вязкоупругими.

В некоторых приложениях делается еще одно грубое разделение на жидкости: идеальные и неидеальные жидкости. Идеальная жидкость не является вязкой и не оказывает никакого сопротивления силе сдвига. Идеальной жидкости действительно не существует, но в некоторых расчетах это предположение оправдано. Одним из примеров этого является течение вдали от твердых поверхностей. Во многих случаях вязкие эффекты сосредоточены вблизи твердых границ (например, в пограничных слоях), в то время как в областях поля течения, удаленных от границ, вязкими эффектами можно пренебречь, и жидкость там рассматривается как невязкая (идеальная поток). В пренебрежении вязкостью член, содержащий тензор вязких напряжений ${\displaystyle \mathbf {\tau } }$ в уравнении Навье – Стокса обращается в нуль. Приведенное в таком виде уравнение называется Уравнение Эйлера.

Смотрите также

• Физический портал

• Аэродинамика
• Прикладная механика
• Принцип Бернулли
• Сообщающиеся сосуды
• Вычислительная гидродинамика
• Скорректированный расход топлива
• Вторичный поток
• Различные типы граничных условий в гидродинамике

Рекомендации

1. Уайт, Фрэнк М. (2011). Механика жидкости (7-е изд.). Макгроу-Хилл. ISBN  978-0-07-352934-9.
2. Ту, Цзиюань; Йео, Гуань Хэн; Лю, Чаокун (21 ноября 2012 г.). Вычислительная гидродинамика: практический подход. ISBN  978-0080982434.
3. Бэтчелор, К. К., & Бэтчелор, Г. К. (2000). Введение в гидродинамику. Издательство Кембриджского университета.
4. Бертин, Дж. Дж., И Смит, М. Л. (1998). Аэродинамика для инженеров (Том 5). Река Аппер Сэдл, Нью-Джерси: Prentice Hall.
5. Андерсон-младший, Дж. Д. (2010). Основы аэродинамики. Тата Макгроу-Хилл Образование.
6. Хоутон, Э. Л., и Карпентер, П. В. (2003). Аэродинамика для студентов инженерных специальностей. Эльзевир.
7. Милн-Томсон, Л. М. (1973). Теоретическая аэродинамика. Курьерская корпорация.
8. Милн-Томсон, Л. М. (1996). Теоретическая гидродинамика. Курьерская корпорация.
9. Биркгоф, Г. (2015). Гидродинамика. Издательство Принстонского университета.
10. Бэтчелор, Джордж К. (1967). Введение в динамику жидкости. Издательство Кембриджского университета. п. 74. ISBN  0-521-66396-2.
11. Гринкорн, Роберт (3 октября 2018 г.). Основы импульса, тепла и массообмена. CRC Press. п. 18. ISBN  978-1-4822-9297-8.
12. Константин П. и Фойас К. (1988). Уравнения Навье-Стокса. Издательство Чикагского университета.
13. Темам, Р. (2001). Уравнения Навье-Стокса: теория и численный анализ (Том 343). Американское математическое общество.
14. Фойас, К., Мэнли, О., Роза, Р., и Темам, Р. (2001). Уравнения Навье-Стокса и турбулентность (Том 83). Издательство Кембриджского университета.
15. Жиро, В., и Равиар, П. А. (2012). Методы конечных элементов для уравнений Навье-Стокса: теория и алгоритмы (Том 5). Springer Science & Business Media.
16. Андерсон, Дж. Д., и Вендт, Дж. (1995). Вычислительная гидродинамика (Том 206). Нью-Йорк: Макгроу-Хилл.
17. Чанг, Т. Дж. (2010). Вычислительная гидродинамика. Издательство Кембриджского университета.
18. Блазек, Дж. (2015). Вычислительная гидродинамика: принципы и приложения. Баттерворт-Хайнеманн.
19. Весселинг, П. (2009). Принципы вычислительной гидродинамики (Том 29). Springer Science & Business Media.
20. Андерсон Д., Таннехилл Дж. К. и Плетчер Р. Х. (2016). Вычислительная механика жидкости и теплопередача. Тейлор и Фрэнсис.
21. Kundu, Pijush K .; Коэн, Ира М .; Доулинг, Дэвид Р. «10». Механика жидкости (6-е изд.). Академическая пресса. ISBN  978-0124059351.

дальнейшее чтение

• Фалькович, Григорий (2011), Механика жидкости (краткий курс для физиков), Издательство Кембриджского университета, Дои:10.1017 / CBO9780511794353, ISBN  978-1-107-00575-4
• Kundu, Pijush K .; Коэн, Ира М. (2008), Механика жидкости (4-е пересмотренное издание), Academic Press, ISBN  978-0-12-373735-9
• Карри, И. Г. (1974), Фундаментальная механика жидкостей, McGraw-Hill, Inc., ISBN  0-07-015000-1
• Massey, B .; Уорд-Смит, Дж. (2005), Механика жидкостей (8-е изд.), Тейлор и Фрэнсис, ISBN  978-0-415-36206-1
• Назаренко, Сергей (2014), Гидродинамика на примерах и решениях, CRC Press (группа Тейлор и Фрэнсис), ISBN  978-1-43-988882-7

внешняя ссылка

• Бесплатные книги по механике жидкостей
• Ежегодный обзор гидромеханики
• CFDWiki - справочник по вычислительной гидродинамике.
• Образовательная скорость изображения частиц - ресурсы и демонстрации