Теорема о разделении гиперплоскостей - Hyperplane separation theorem - Wikipedia

Иллюстрация теоремы об отделении гиперплоскостей.

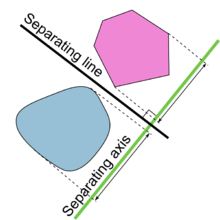
В геометрия, то теорема об отделении гиперплоскостей это теорема о непересекающийся выпуклые множества в п-размерный Евклидово пространство. Есть несколько довольно похожих версий. В одной из версий теоремы, если оба эти множества закрыто и хотя бы один из них компактный, то есть гиперплоскость между ними и даже две параллельные гиперплоскости между ними, разделенные промежутком. В другой версии, если оба непересекающихся выпуклых множества открыты, то между ними есть гиперплоскость, но не обязательно какой-либо зазор. Ось, ортогональная разделяющей гиперплоскости, называется разделительная ось, поскольку ортогональные прогнозы выпуклых тел на ось не пересекаются.

Теорема об отделении гиперплоскостей возникает из-за Герман Минковски. В Теорема Хана – Банаха об отделимости обобщает результат на топологические векторные пространства.

Связанный результат - поддерживающая теорема о гиперплоскости.

В контексте машины опорных векторов, то оптимально разделяющая гиперплоскость или же гиперплоскость с максимальным запасом это гиперплоскость который разделяет два выпуклые оболочки очков и равноудаленный из двух.^[1][2][3]

Заявления и доказательства

Теорема о разделении гиперплоскостей^[4] — Позволять А и B - два непересекающихся непустых выпуклых подмножества р^п. Тогда существует ненулевой вектор v и реальное число c такой, что

${\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}$

для всех Икс в А и у в B; т.е. гиперплоскость ${\displaystyle \langle \cdot ,v\rangle =c}$, v нормальный вектор, разделяет А и B.

Доказательство основано на следующей лемме.

Лемма — Позволять ${\displaystyle K}$ - непустое замкнутое выпуклое подмножество р^п. Тогда существует единственный вектор в ${\displaystyle K}$ минимальной нормы (длины).

Доказательство леммы: Позволять ${\displaystyle \delta =\inf\{|x|:x\in K\}.}$ Позволять ${\displaystyle x_{j}}$ быть последовательностью в ${\displaystyle K}$ такой, что ${\displaystyle |x_{j}|\to \delta }$. Обратите внимание, что ${\displaystyle (x_{i}+x_{j})/2}$ в ${\displaystyle K}$ поскольку ${\displaystyle K}$ выпуклый и поэтому ${\displaystyle |x_{i}+x_{j}|^{2}\geq 4\delta ^{2}}$.С

${\displaystyle |x_{i}-x_{j}|^{2}=2|x_{i}|^{2}+2|x_{j}|^{2}-|x_{i}+x_{j}|^{2}\leq 2|x_{i}|^{2}+2|x_{j}|^{2}-4\delta ^{2}\to 0}$

в качестве ${\displaystyle i,j\to \infty }$, ${\displaystyle x_{i}}$ это Последовательность Коши и так имеет предел Икс в ${\displaystyle K}$. Он уникален, поскольку если у в ${\displaystyle K}$ и имеет норму δ, то${\displaystyle |x-y|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0}$ и Икс = у. ${\displaystyle \square }$

Доказательство теоремы: Даны непересекающиеся непустые выпуклые множества А, B, позволять

${\displaystyle K=A+(-B)=\{x-y\mid x\in A,y\in B\}.}$

С ${\displaystyle -B}$ выпуклый, а сумма выпуклых множеств выпукло, ${\displaystyle K}$ выпуклый. По лемме замыкание ${\displaystyle {\overline {K}}}$ из ${\displaystyle K}$, которая является выпуклой, содержит вектор ${\displaystyle v}$ минимальной нормы. С ${\displaystyle {\overline {K}}}$ выпукло, для любого ${\displaystyle n}$ в ${\displaystyle K}$, отрезок линии

${\displaystyle v+t(n-v),\,0\leq t\leq 1}$

лежит в ${\displaystyle {\overline {K}}}$ и так

${\displaystyle |v|^{2}\leq |v+t(n-v)|^{2}=|v|^{2}+2t\langle v,n-v\rangle +t^{2}|n-v|^{2}}$.

За ${\displaystyle 0<t\leq 1}$, то есть:

${\displaystyle 0\leq 2\langle v,n\rangle -2|v|^{2}+t|n-v|^{2}}$

и позволяя ${\displaystyle t\to 0}$ дает: ${\displaystyle \langle n,v\rangle \geq |v|^{2}}$. Следовательно, для любого x из А и у в B, у нас есть: ${\displaystyle \langle x-y,v\rangle \geq |v|^{2}}$. Таким образом, если v отлична от нуля, доказательство завершено, так как

${\displaystyle \inf _{x\in A}\langle x,v\rangle \geq |v|^{2}+\sup _{y\in B}\langle y,v\rangle .}$

В более общем плане (охватывая случай v = 0), сначала рассмотрим случай, когда внутренность ${\displaystyle K}$ непусто. Внутренность исчерпывается вложенной последовательностью непустых компактных выпуклых подмножеств ${\displaystyle K_{1}\subset K_{2}\subset K_{3}\subset \cdots }$. Поскольку 0 отсутствует в ${\displaystyle K}$, каждый ${\displaystyle K_{n}}$ содержит ненулевой вектор ${\displaystyle v_{n}}$ минимальной длины и, согласно аргументам в начале, мы имеем: ${\displaystyle \langle x,v_{n}\rangle \geq 0}$ для любого ${\displaystyle x\in K_{n}}$. Мы можем нормализовать ${\displaystyle v_{n}}$иметь длину один. Тогда последовательность ${\displaystyle v_{n}}$ содержит сходящуюся подпоследовательность (поскольку n-сфера компактно) с пределом v, которая не равна нулю. У нас есть ${\displaystyle \langle x,v\rangle \geq 0}$ для любого Икс в интерьере ${\displaystyle K}$ и по непрерывности то же самое верно для всех Икс в ${\displaystyle K}$. Завершим доказательство, как и раньше. Наконец, если ${\displaystyle K}$ имеет пустой интерьер, аффинное множество что он охватывает, имеет размер меньше, чем все пространство. как следствие ${\displaystyle K}$ содержится в некоторой гиперплоскости ${\displaystyle \langle \cdot ,v\rangle =c}$; таким образом, ${\displaystyle \langle x,v\rangle \geq c}$ для всех Икс в ${\displaystyle K}$ и завершаем доказательство, как и раньше. ${\displaystyle \square }$

Количество измерений должно быть конечным. В бесконечномерных пространствах есть примеры двух замкнутых выпуклых непересекающихся множеств, которые не могут быть разделены замкнутой гиперплоскостью (гиперплоскостью, где непрерывный линейный функционал равен некоторой константе) даже в слабом смысле, когда неравенства не являются строгими.^[5]

Приведенное выше доказательство также доказывает первую версию теоремы, упомянутой в статье (чтобы увидеть ее, заметьте, что ${\displaystyle K}$ в доказательстве замкнуто при условии следующей теоремы.)

Теорема о разделении I —  Позволять А и B - два непересекающихся непустых замкнутых выпуклых множества, одно из которых компактно. Тогда существует ненулевой вектор v и реальные числа ${\displaystyle c_{1}<c_{2}}$ такой, что

${\displaystyle \langle x,v\rangle >c_{2}\,{\text{ and }}\langle y,v\rangle <c_{1}}$

для всех Икс в А и у в B.

Здесь нельзя ослабить компактность гипотезы; см. пример в следующем разделе. Эта версия теоремы разделения действительно обобщается на бесконечномерность; обобщение более известно как Теорема Хана – Банаха об отделимости.

У нас также есть:

Теорема о разделении II —  Позволять А и B - два непересекающихся непустых выпуклых множества. Если А открыто, то существует ненулевой вектор v и реальное число ${\displaystyle c}$ такой, что

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle \leq c}$

для всех Икс в А и у в B. Если оба множества открыты, то существует ненулевой вектор v и реальное число ${\displaystyle c}$ такой, что

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle <c}$

для всех Икс в А и у в B.

Это следует из стандартного варианта, поскольку разделяющая гиперплоскость не может пересекать внутренности выпуклых множеств.

Обратное к теореме

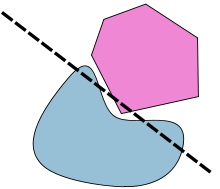
Заметим, что существование гиперплоскости, которая только «разделяет» два выпуклых множества в слабом смысле нестрогости обоих неравенств, очевидно, не означает, что эти два множества не пересекаются. Оба набора могут иметь точки, расположенные на гиперплоскости.

Контрпримеры и уникальность

В теорема не применяется если одно из тел невыпуклое.

Если один из А или же B невыпукло, то есть много возможных контрпримеров. Например, А и B могли быть концентрические круги. Более тонкий контрпример - это тот, в котором А и B оба закрыты, но ни один из них не является компактным. Например, если А является замкнутой полуплоскостью и B ограничен одним плечом гиперболы, то строго разделяющей гиперплоскости не существует:

${\displaystyle A=\{(x,y):x\leq 0\}}$

${\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }$

(Хотя, согласно примеру второй теоремы, существует гиперплоскость, разделяющая их внутренности.) Другой тип контрпримера имеет А компактный и B открыто. Например, A может быть замкнутым квадратом, а B может быть открытым квадратом, который касается А.

В первой версии теоремы, очевидно, разделяющая гиперплоскость никогда не бывает единственной. Во второй версии он может быть уникальным, а может и не быть. Технически разделительная ось никогда не бывает уникальной, потому что ее можно перемещать; во второй версии теоремы разделяющая ось может быть единственной с точностью до сдвига.

Использование при обнаружении столкновений

Теорема о разделяющей оси (SAT) говорит, что:

Два выпуклых объекта не перекрываются, если существует линия (называемая осью), на которую проекции двух объектов не перекрываются.

SAT предлагает алгоритм проверки того, пересекаются ли два выпуклых тела или нет.

Независимо от размерности, разделительная ось всегда является линией. Например, в 3D пространство разделено плоскостями, но разделительная ось перпендикулярна разделительной плоскости.

Теорема о разделяющей оси может быть применена для быстрого обнаружение столкновения между полигональными сетками. Каждый лицо с нормальный или другое направление объекта используется как разделительная ось, а также в качестве перекрестных произведений. Обратите внимание, что это дает возможные разделяющие оси, а не разделяющие линии / плоскости.

Если бы перекрестные произведения не использовались, определенные случаи без столкновения «ребро-кромка» рассматривались бы как конфликтующие. Для повышения эффективности параллельные оси могут быть рассчитаны как одна ось.

Смотрите также

• Двойной конус
• Лемма Фаркаша
• Теорема Кирхбергера
• Оптимальный контроль

Примечания

1. Хасти, Тревор; Тибширани, Роберт; Фридман, Джером (2008). Элементы статистического обучения: интеллектуальный анализ данных, вывод и прогнозирование (PDF) (Второе изд.). Нью-Йорк: Спрингер. С. 129–135.
2. Виттен, Ян Х .; Франк, Эйбе; Холл, Марка А .; Пал, Кристофер Дж. (2016). Интеллектуальный анализ данных: практические инструменты и методы машинного обучения (Четвертое изд.). Морган Кауфманн. С. 253–254.
3. Дайзенрот, Марк Питер; Фейсал, А. Альдо; Онг, Ченг Сун (2020). Математика для машинного обучения. Издательство Кембриджского университета. С. 337–338. ISBN  978-1-108-45514-5.
4. Бойд и Ванденберге 2004, Упражнение 2.22.
5. Хаим Брезис, Анализируйте функционал: теория и приложения, 1983, remarque 4, с. 7.

Рекомендации

• Бойд, Стивен П .; Ванденберге, Ливен (2004). Выпуклая оптимизация (pdf). Издательство Кембриджского университета. ISBN  978-0-521-83378-3.
• Гольштейн, Э. Г .; Третьяков, Н.В. (1996). Модифицированные лагранжианы и монотонные отображения в оптимизации. Нью-Йорк: Вили. п. 6. ISBN  0-471-54821-9.
• Симидзу, Киётака; Ишизука, Йо; Бард, Джонатан Ф. (1997). Недифференцируемое двухуровневое математическое программирование. Бостон: Kluwer Academic Publishers. п. 19. ISBN  0-7923-9821-1.

внешняя ссылка

• Обнаружение столкновений и ответ