Дополнение Минковского - Minkowski addition

Красная цифра - это сумма Минковского синих и зеленых фигур.

В геометрия, то Сумма Минковского (также известен как расширение ) двух наборы из векторы положения А и B в Евклидово пространство формируется путем добавления каждого вектора в А каждому вектору в B, т.е. множество

${\displaystyle A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}.}$

Аналогично Разница Минковского (или геометрическая разница)^[1] определяется с помощью операция дополнения в качестве

${\displaystyle A-B=(A^{c}+B)^{c}}$

В целом ${\displaystyle A-B\neq A+(-B)}$. Например, в одномерном случае ${\displaystyle A=[-2,2]}$ и ${\displaystyle B=[-1,1]}$ разница Минковского ${\displaystyle A-B=[-1,1]}$, в то время как ${\displaystyle A+(-B)=A+B=[-3,3].}$

В двумерном случае разность Минковского тесно связана с эрозия (морфология) в обработка изображений.

Сумма Минковского А + B

B

А

Концепция названа в честь Герман Минковски.

Пример

Например, если у нас есть два набора А и B, каждый из трех векторов положения (неформально трех точек), представляющих вершины из двух треугольники в ${\displaystyle \mathbb {R} ^{2}}$, с координатами

${\displaystyle A=\{(1,0),(0,1),(0,-1)\}}$

и

${\displaystyle B=\{(0,0),(1,1),(1,-1)\}}$

то их сумма Минковского равна

${\displaystyle A+B=\{(1,0),(2,1),(2,-1),(0,1),(1,2),(1,0),(0,-1),(1,0),(1,-2)\}}$

который состоит из вершин шестиугольника.

Для Минковского добавление нулевой набор, {0}, содержащий только нулевой вектор, 0, является элемент идентичности: для каждого подмножества S векторного пространства,

${\displaystyle S+\{0\}=S.}$

В пустой набор важно в сложении Минковского, потому что пустое множество уничтожает все остальные подмножества: для каждого подмножества S векторного пространства, его сумма с пустым множеством пуста:

${\displaystyle S+\emptyset =\emptyset .}$

в выпуклый корпус красного набора каждая синяя точка является выпуклое сочетание некоторых красных точек.

Дополнение Минковского наборов. Сумма квадратов Q₁=[0,1]² и Q₂=[1,2]² это квадрат Q₁+Q₂=[1,3]².

Выпуклые оболочки сумм Минковского

Сложение Минковского хорошо себя ведет в отношении операции взятия выпуклые оболочки, как показывает следующее предложение:

• Для всех непустых подмножеств S₁ и S₂ вещественного векторного пространства, выпуклая оболочка их суммы Минковского является суммой Минковского их выпуклых оболочек:

${\displaystyle \operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).}$

Этот результат верен в более общем случае для любого конечного набора непустых множеств:

${\displaystyle \operatorname {Conv} \left(\sum {S_{n}}\right)=\sum \operatorname {Conv} (S_{n}).}$

В математической терминологии операции суммирования Минковского и формирования выпуклые оболочки находятся поездка на работу операции.^[2][3]

Если S выпуклое множество, то ${\displaystyle \mu S+\lambda S}$ также выпуклое множество; более того

${\displaystyle \mu S+\lambda S=(\mu +\lambda )S}$

для каждого ${\displaystyle \mu ,\lambda \geq 0}$. И наоборот, если это "распределительное свойство "выполняется для всех неотрицательных действительных чисел, ${\displaystyle \mu ,\lambda }$, то множество выпукло.^[4]

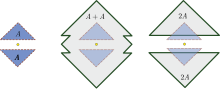
На рисунке показан пример невыпуклого множества, для которого А + А ⊋ 2А.

Пример невыпуклого множества, такого что А + А ≠ 2А

Пример в одном измерении: B= [1,2] ∪ [4,5]. Нетрудно подсчитать, что 2B= [2,4] ∪ [8,10] но B+B= [2,4] ∪ [5,7] ∪ [8,10], поэтому снова B+B ⊋ 2B.

Суммы Минковского действуют линейно на периметре двумерных выпуклых тел: периметр суммы равен сумме периметров. Кроме того, если K является (внутренним) a кривая постоянной ширины, то сумма Минковского K а его поворот на 180 ° представляет собой диск. Эти два факта можно объединить, чтобы получить краткое доказательство Теорема Барбье по периметру кривых постоянной ширины.^[5]

Приложения

Минковский играет центральную роль в математическая морфология. Возникает в парадигма мазка и кисти из 2D компьютерная графика (с различным использованием, в частности Дональд Э. Кнут в Метафонт ), а как сплошная развертка операция по 3D компьютерная графика. Также было показано, что он тесно связан с Дистанция движителя земли, и, соответственно, оптимальный транспорт.^[6]

Планирование движения

Суммы Минковского используются в планирование движения объекта среди препятствий. Они используются для вычисления конфигурационное пространство, который представляет собой набор всех допустимых положений объекта. В простой модели поступательного движения объекта в плоскости, где положение объекта может быть однозначно задано положением фиксированной точки этого объекта, пространство конфигурации представляет собой сумму Минковского множества препятствий и подвижного объекта. объект помещен в начало координат и повернут на 180 градусов.

Обработка с числовым программным управлением (ЧПУ)

В числовое управление обработка, программирование инструмента ЧПУ использует тот факт, что сумма Минковского отрезной кусок своей траекторией придает форму прорези в материале.

3D твердотельное моделирование

В OpenSCAD Суммы Минковского используются, чтобы очертить фигуру другой фигурой, создавая композицию обеих фигур.

Теория агрегации

Суммы Минковского также часто используются в теории агрегирования, когда отдельные объекты, подлежащие агрегированию, характеризуются посредством множеств.^[7][8]

Обнаружение столкновений

Суммы Минковского, особенно разности Минковского, часто используются вместе с Алгоритмы GJK вычислить обнаружение столкновения для выпуклой оболочки в физические двигатели.

Алгоритмы вычисления сумм Минковского

Сложение Минковского и выпуклые оболочки. Шестнадцать темно-красных точек (справа) образуют сумму Минковского четырех невыпуклых множеств (слева), каждое из которых состоит из пары красных точек. Их выпуклые корпуса (заштрихованные розовым цветом) содержат знаки плюса (+): правый знак плюса - это сумма левых знаков плюса.

Планарный корпус

Два выпуклых многоугольника на плоскости

Для двух выпуклые многоугольники п и Q в самолете с м и п вершин, их сумма Минковского представляет собой выпуклый многоугольник с не более чем м + п вершин и может быть вычислена за время O (м + п) с помощью очень простой процедуры, которую можно неформально описать следующим образом. Предположим, что края многоугольника заданы и направление, скажем, против часовой стрелки, вдоль границы многоугольника. Тогда легко увидеть, что эти ребра выпуклого многоугольника упорядочены по формуле полярный угол. Разрешите нам объединить упорядоченные последовательности направленных кромок от п и Q в единую упорядоченную последовательность S. Представьте, что эти края твердые стрелки которые можно свободно перемещать, сохраняя при этом их параллельность первоначальному направлению. Соберите эти стрелки в порядке последовательности S прикрепив хвостик следующей стрелки к головке предыдущей стрелки. Оказывается, в результате многоугольная цепь на самом деле будет выпуклым многоугольником, который является суммой Минковского п и Q.

Другой

Если один многоугольник выпуклый, а другой - нет, сложность их суммы Минковского составляет O (nm). Если оба они невыпуклые, сложность их суммы Минковского равна O ((mn)²).

Существенная сумма Минковского

Есть еще понятие существенная сумма Минковского +_е двух подмножеств евклидова пространства. Обычная сумма Минковского может быть записана как

${\displaystyle A+B=\{z\in \mathbb {R} ^{n}\,|\,A\cap (z-B)\neq \emptyset \}.}$

Таким образом существенная сумма Минковского определяется

${\displaystyle A+_{\mathrm {e} }B=\{z\in \mathbb {R} ^{n}\,|\,\mu \left[A\cap (z-B)\right]>0\},}$

куда μ обозначает п-размерный Мера Лебега. Причиной появления термина «существенный» является следующее свойство индикаторные функции: пока

${\displaystyle 1_{A\,+\,B}(z)=\sup _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),}$

видно, что

${\displaystyle 1_{A\,+_{\mathrm {e} }\,B}(z)=\mathop {\mathrm {ess\,sup} } _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),}$

где "ess sup" обозначает существенный супремум.

L^п Сумма Минковского

За K и L компактные выпуклые подмножества в ${\displaystyle \mathbb {R} ^{n}}$, сумма Минковского описывается функция поддержки выпуклых множеств:

${\displaystyle h_{K+L}=h_{K}+h_{L}.}$

За р ≥ 1, Firey^[9] определил L^п Сумма Минковского K +_пL компактных выпуклых множеств K и L в ${\displaystyle \mathbb {R} ^{n}}$ содержащий происхождение как

${\displaystyle h_{K+_{p}L}^{p}=h_{K}^{p}+h_{L}^{p}.}$

Посредством Неравенство Минковского, функция час_{K +пL} снова положительно однородна и выпукла и, следовательно, опорная функция компакта выпуклой. Это определение является основным в L^п Теория Брунна-Минковского.

Смотрите также

• Сумма Бляшке
• Теорема Брунна – Минковского., неравенство об объемах сумм Минковски
• Свертка
• Расширение
• Эрозия
• Интервальная арифметика
• Смешанный объем (a.k.a. Quermassintegral или же собственный объем )
• Параллельная кривая
• Лемма Шепли – Фолкмана.
• Топологическое векторное пространство # Свойства
• Зонотоп

Примечания

1. Хадвигер, Хьюго (1950), "Minkowskische Addition und Subtraktion trustbiger Punktmengen und die Theoreme von Erhard Schmidt", Математика. Z., 53 (3): 210–218, Дои:10.1007 / BF01175656
2. Теорема 3 (страницы 562–563): Крейн, М.; Шмулян В. (1940). «О правильно выпуклых множествах в пространстве, сопряженном с банаховым пространством». Анналы математики. Вторая серия. 41. С. 556–583. Дои:10.2307/1968735. JSTOR  1968735. МИСТЕР  0002009.
3. Для коммутативности сложения Минковского и выпуклость см. теорему 1.1.2 (стр. 2–3) у Шнайдера; в этой ссылке обсуждается большая часть литературы по выпуклые оболочки Минковского суммы в «Главе 3, добавление Минковского» (страницы 126–196): Шнайдер, Рольф (1993). Выпуклые тела: теория Брунна – Минковского.. Энциклопедия математики и ее приложений. 44. Кембридж: Издательство Кембриджского университета. С. xiv + 490. ISBN  978-0-521-35220-8. МИСТЕР  1216521.
4. Глава 1: Шнайдер, Рольф (1993). Выпуклые тела: теория Брунна – Минковского.. Энциклопедия математики и ее приложений. 44. Кембридж: Издательство Кембриджского университета. С. xiv + 490. ISBN  978-0-521-35220-8. МИСТЕР  1216521.
5. Теорема Барбье (Ява) в завязать узел.
6. Клайн, Джеффри (2019). «Свойства d-мерной задачи землекопа». Дискретная прикладная математика. 265: 128–141. Дои:10.1016 / j.dam.2019.02.042.
7. Зеленюк, В (2015). «Агрегация масштабной эффективности». Европейский журнал операционных исследований. 240 (1): 269–277. Дои:10.1016 / j.ejor.2014.06.038.
8. Mayer, A .; Зеленюк, В. (2014). «Агрегация показателей производительности Мальмквиста с учетом перераспределения ресурсов». Европейский журнал операционных исследований. 238 (3): 774–785. Дои:10.1016 / j.ejor.2014.04.003.
9. Файери, Уильям Дж. (1962) "п-средства выпуклых тел », Математика. Сканд., 10: 17–24, Дои:10.7146 / math.scand.a-10510

Рекомендации

• Эрроу, Кеннет Дж.; Хан, Фрэнк Х. (1980). Общий конкурентный анализ. Учебники по экономике. 12 (перепечатка (1971) Сан-Франциско, Калифорния: Holden-Day, Inc. Тексты по математической экономике.6 ред.). Амстердам: Северная Голландия. ISBN  978-0-444-85497-1. МИСТЕР  0439057.
• Гарднер, Ричард Дж. (2002), "Неравенство Брунна-Минковского", Бык. Амер. Математика. Soc. (Н.С.), 39 (3): 355–405 (электронная), Дои:10.1090 / S0273-0979-02-00941-2
• Грин, Джерри; Хеллер, Уолтер П. (1981). «1 Математический анализ и выпуклость с приложениями к экономике». В Стрелка, Кеннет Джозеф; Intriligator, Майкл Д. (ред.). Справочник по математической экономике, Томя. Справочники по экономике. 1. Амстердам: Издательство Северной Голландии, стр. 15–52. Дои:10.1016 / S1573-4382 (81) 01005-9. ISBN  978-0-444-86126-9. МИСТЕР  0634800.
• Генри Манн (1976), Теоремы сложения: теоремы сложения теории групп и теории чисел (Исправленная перепечатка изд. Wiley 1965 г.), Хантингтон, Нью-Йорк: издательство Robert E. Krieger Publishing Company, ISBN  978-0-88275-418-5 - через http://www.krieger-publishing.com/subcats/Mat MathematicsandStatistics/mat Mathematicsandstatistics.html
• Рокафеллар, Р. Тиррелл (1997). Выпуклый анализ. Ориентиры Принстона в математике (Перепечатка серии математических исследований Принстона 1979 г.28 ред.). Принстон, Нью-Джерси: Издательство Принстонского университета. С. xviii + 451. ISBN  978-0-691-01586-6. МИСТЕР  1451876.
• Натансон, Мелвин Б. (1996), Аддитивная теория чисел: обратные задачи и геометрия сумм, GTM, 165, Спрингер, Zbl  0859.11003.
• Окс, Эдуард; Шарир, Миха (2006), "Суммы Минковского монотонных и простых многоугольников", Дискретная и вычислительная геометрия, 35 (2): 223–240, Дои:10.1007 / s00454-005-1206-у.
• Шнайдер, Рольф (1993), Выпуклые тела: теория Брунна-Минковского, Кембридж: Издательство Кембриджского университета.
• Тао, Теренс и Ву, Ван (2006), Аддитивная комбинаторика, Издательство Кембриджского университета.
• Mayer, A .; Зеленюк, В. (2014). «Агрегация показателей производительности Мальмквиста с учетом перераспределения ресурсов». Европейский журнал операционных исследований. 238 (3): 774–785. Дои:10.1016 / j.ejor.2014.04.003.
• Зеленюк, В (2015). «Агрегация масштабной эффективности». Европейский журнал операционных исследований. 240 (1): 269–277. Дои:10.1016 / j.ejor.2014.06.038.

внешняя ссылка

• «Сложение Минковского», Энциклопедия математики, EMS Press, 2001 [1994]
• Хау, Роджер (1979), О тенденции к выпуклости векторной суммы множеств, Документы для обсуждения Фонда Коулза, 538, Фонд Коулза для исследований в области экономики, Йельский университет
• Суммы Минковского, в Библиотека алгоритмов вычислительной геометрии
• Сумма Минковского двух треугольников и Сумма Минковского диска и многоугольника Джордж Бек, Демонстрационный проект Wolfram.
• Добавление Минковского выпуклых форм к Александр Богомольный: апплет
• Викиучебники: Руководство пользователя OpenSCAD / Преобразования # minkowski Мариус Кинтель: Приложение