Законы формы - Laws of Form
Законы формы (далее LoF) - это книга Г. Спенсер-Браун, опубликованный в 1969 году, который пересекает границу между математика и философия. LoF описывает три различных логические системы:
- «Первичная арифметика» (описанная в главе 4 LoF), модели которых включают Логическая арифметика;
- Главная алгебра "(Глава 6 LoF), чья модели включить двухэлементная булева алгебра (далее сокращенно 2), Логическая логика, а классический пропозициональное исчисление;
- «Уравнения второй степени» (глава 11), чьи интерпретации включают конечные автоматы и Церковь Алонсо Ограниченная рекурсивная арифметика (RRA).
"Граничная алгебра" принадлежит Мегуайру (2011)[1] термин для объединения первичной алгебры и первичной арифметики. Законы формы иногда свободно относится к «первичной алгебре», а также к LoF.
Книга
Эта секция нужны дополнительные цитаты для проверка. (Ноябрь 2018) (Узнайте, как и когда удалить этот шаблон сообщения) |
В предисловии говорится, что работа была впервые исследована в 1959 году, и Спенсер Браун цитирует Бертран Рассел как поддержку его начинанию. Он также благодарит Дж. С. П. Миллер из Университетский колледж Лондона за помощь с корректурой и другие рекомендации. В 1963 году Спенсера Брауна пригласил Гарри Фрост, штатный преподаватель кафедры физических наук кафедры заочного обучения Лондонский университет читать курс математики логики.
LoF возникла в результате работы в области электронной инженерии, которую его автор сделал около 1960 года, и из последующих лекций по математическая логика он дал под эгидой Лондонский университет программа расширения. LoF вышла в нескольких выпусках. Вторая серия изданий появилась в 1972 году с «Предисловием к первому американскому изданию», в котором подчеркивалось использование парадоксов самореференции.[2] самым последним из них был немецкий перевод 1997 года, который никогда не выходил из печати.
Математика заполняет только около 55 пикселей и довольно элементарна.[оригинальное исследование? ] Но LoF 'мистическая и декламационная проза, и ее любовь к парадокс, сделать его трудным для всех. Спенсер-Браун находился под влиянием Витгенштейн и Р. Д. Лэнг. LoF также перекликается с рядом тем из сочинений Чарльз Сандерс Пирс, Бертран Рассел, и Альфред Норт Уайтхед.
Вся книга написана оперативно, давая читателю инструкции вместо того, чтобы рассказывать ему, что «есть». В соответствии с интересом Дж. Спенсер-Брауна к парадоксам, единственное предложение, которое делает утверждение, что что-то есть, - это утверждение, в котором говорится, что такие утверждения не используются в этой книге.[3] За исключением этого предложения, книгу можно рассматривать как пример E-Prime.
Прием
Якобы произведение формальной математики и философии, LoF стал чем-то вроде культовая классика: похвалил Хайнц фон Ферстер когда он рассмотрел это для Каталог всей Земли.[4] Согласные указывают на LoF как воплощение загадочной "математики сознание ", его алгебраический символизм захватывает (возможно, даже") неявный корень познание: умение «различать». LoF утверждает, что первичная алгебра обнаруживает разительную связь между логика, Булева алгебра, арифметика и философия языка и разум.
Банашевский (1977)[5] утверждает, что первичная алгебра - не что иное, как новые обозначения для булевой алгебры. Действительно, двухэлементная булева алгебра 2 можно рассматривать как предполагаемую интерпретацию первичной алгебры. Но все же обозначения первичной алгебры:
- Полностью использует двойственность характеризуя не только Булевы алгебры но все решетки;
- Подчеркивает, насколько синтаксически различные утверждения в логике и 2 может иметь идентичный семантика;
- Значительно упрощает вычисления булевой алгебры и доказательства в приговор и силлогистический логика.
Более того, синтаксис первичной алгебры может быть расширен на формальные системы, отличные от 2 и сентенциальная логика, приводящая к граничной математике (см. связанные работы ниже).
LoF оказал влияние, среди прочего, Хайнц фон Ферстер, Луи Кауфман, Никлас Луман, Умберто Матурана, Франсиско Варела и Уильям Бриккен. Некоторые из этих авторов изменили первичную алгебру множеством интересных способов.
LoF утверждал, что некоторые хорошо известные математические гипотезы очень давно, такие как Теорема о четырех цветах, Последняя теорема Ферма, а Гипотеза Гольдбаха, доказуемы с помощью расширений первичной алгебры. Спенсер-Браун в конце концов распространил предполагаемое доказательство теоремы о четырех цветах, но оно встретило скептицизм.[6]
Форма (Глава 1)
Символ:
Также называемый «знаком» или «крестом», это основная черта Законов Формы. В неповторимой и загадочной моде Спенсер-Брауна Знак символизирует корень познание, т.е. дуалистический Знак указывает на возможность отличить «это» от «всего остального». но этот".
В LoF, Крест обозначает «различие», и его можно рассматривать как обозначающее сразу следующее:
- Акт проведения границы вокруг чего-либо, таким образом отделяя это от всего остального;
- То, что становится отличным от всего, проводя границы;
- Переход с одной стороны границы на другую.
Все три способа подразумевают действие со стороны когнитивной сущности (например, человека), проводящей различие. Так как LoF кладет это:
«Первая команда:
- Проведите различие
вполне можно выразить такими способами, как:
- Пусть будет различие,
- Найдите различие,
- Смотрите различие,
- Опишите различие,
- Определите различие,
Или:
- Пусть будет проведено различие ". (LoF, Примечания к главе 2)
Контрапунктом для отмеченного состояния является состояние Unmarked, которое представляет собой просто ничто, пустоту или невыразимое бесконечное, представленное пробелом. Это просто отсутствие Креста. Никаких различий и пересечений не проводилось. Отмеченное состояние и пустота - два примитивных значения Законов Формы.
Крест можно рассматривать как обозначение различия между двумя состояниями: одно «рассматривается как символ», а другое не рассматривается. Из этого факта возникает любопытный резонанс с некоторыми теориями сознание и язык. Как это ни парадоксально, Форма одновременно является Наблюдателем и Наблюдаемым, а также является творческим актом проведения наблюдения. LoF (исключая заднюю часть) закрывается словами:
... первое различие, Знак и наблюдатель не только взаимозаменяемы, но и идентичны по форме.
К. С. Пирс пришел к похожему пониманию в 1890-х; увидеть § Связанных с работой.
Первичная арифметика (Глава 4)
В синтаксис первичной арифметики выглядит следующим образом. Всего два атомарные выражения:
- Пустой крест
 ;
; - Пустая страница полностью или частично («пустота»).
Есть два индуктивных правила:
- Крест
 может быть написано поверх любого выражения;
может быть написано поверх любого выражения; - Любые два выражения могут быть соединенный.
В семантика первичной арифметики, пожалуй, не что иное, как единственный явный определение в LoF: «Различие - совершенное воздержание».
Пусть «немаркированное состояние» будет синонимом пустоты. Пусть пустой Крест обозначает «отмеченное состояние». Перекрестие означает переход от одного значения, неотмеченного или отмеченного состояния, к другому. Теперь мы можем сформулировать «арифметический» аксиомы A1 и A2, на которых основана первичная арифметика (и, следовательно, все законы формы):
«А1. Закон призвания». Двойной вызов из состояния неотличим от однократного вызова. Дважды провести различие дает тот же эффект, что и один раз. Например, сказать «Да будет свет», а затем снова сказать «Да будет свет» - все равно, что сказать это один раз. Формально:
«A2. Закон пересечения». После перехода из немаркированного состояния в отмеченное, повторное пересечение («повторное пересечение»), начиная с отмеченного состояния, возвращает единицу в немаркированное состояние. Следовательно, обратное пересечение аннулирует пересечение. Формально:
И в A1, и в A2 выражение справа от '=' содержит меньше символов, чем выражение слева от '='. Это говорит о том, что каждое первичное арифметическое выражение при повторном применении А1 и А2 может быть упрощенный в одно из двух состояний: отмеченное или немаркированное состояние. Это действительно так, и результатом является «упрощение» выражения. Две фундаментальные метатеоремы первичной арифметики утверждают, что:
- Каждое конечное выражение имеет уникальное упрощение. (T3 в LoF);
- Начиная с начального отмеченного или немаркированного состояния, «усложнение» выражения конечным числом повторных применений A1 и A2 не может привести к выражению, упрощение которого отличается от начального состояния. (T4 в LoF).
Таким образом связь из логическая эквивалентность перегородки все первичные арифметические выражения на два классы эквивалентности: те, которые упрощают до Креста, и те, которые упрощают до пустоты.
A1 и A2 имеют свободные аналоги в свойствах последовательных и параллельных электрических цепей, а также в других способах построения диаграмм процессов, включая блок-схемы. A1 соответствует параллельному соединению, а A2 - последовательному соединению, при том понимании, что различение соответствует изменению способа соединения двух точек в цепи, а не просто добавлению проводки.
Первичная арифметика аналогична следующим формальным языкам из математика и Информатика:
- А Язык Дайка порядка 1 с нулевым алфавитом;
- Простейший контекстно-свободный язык в Иерархия Хомского;
- А переписать систему это сильно нормализующий и сливаться.
Фраза «исчисление показаний» в LoF является синонимом «первичной арифметики».
Понятие канона
Концепция, свойственная LoF это "каноник". В то время как LoF не определяет канон, следующие два отрывка из Примечаний к гл. 2 подходят:
Более важные структуры командования иногда называют каноны. Это способы, которыми руководящие предписания, кажется, группируются в созвездия, и, таким образом, никоим образом не являются независимыми друг от друга. Канон отличается тем, что находится вне (то есть, описывает) строящуюся систему, но команда строить (например, «провести различие»), даже если она может иметь центральное значение, не является каноном. Канон - это приказ или набор приказов, которые разрешают или разрешают, но не создают или создают.
... основная форма математической коммуникации - это не описание, а предписание ... Музыка - это похожая форма искусства, композитор даже не пытается описать набор звуков, которые он имеет в виду, а тем более набор чувств, вызванных ими , но записывает набор команд, которые, если исполнитель им подчиняется, могут привести к воспроизведению для слушателя первоначального опыта композитора.
Эти отрывки относятся к различию в металогия между объектный язык, формальный язык обсуждаемой логической системы, и метаязык, язык (часто естественный язык), отличный от объектного языка, используемый для описания и обсуждения объектного языка. Первая цитата, кажется, утверждает, что каноны являются частью метаязыка. Вторая цитата, кажется, утверждает, что утверждения на объектном языке, по сути, являются командами, адресованными читателю автором. Ни то и другое утверждение не выполняется в стандартной металогике.
Первичная алгебра (глава 6)
Синтаксис
Для любого действительного первичного арифметического выражения вставьте в одно или несколько мест любое количество латинских букв с необязательными числовыми индексами; результат - первичная алгебра формула. Письма, используемые в математика и логика называются переменные. Переменная первичной алгебры указывает место, где можно записать примитивное значение ![]() или его дополнение
или его дополнение ![]() . Несколько экземпляров одной и той же переменной обозначают несколько местоположений одного и того же примитивного значения.
. Несколько экземпляров одной и той же переменной обозначают несколько местоположений одного и того же примитивного значения.
Правила логической эквивалентности
Знак '=' может связывать два логически эквивалентных выражения; результат уравнение. Под «логически эквивалентным» понимается то, что два выражения имеют одинаковое упрощение. Логическая эквивалентность является отношение эквивалентности над множеством формул первичной алгебры, управляемой правилами R1 и R2. Пусть «C» и «D» будут формулами, каждая из которых содержит хотя бы один экземпляр подформулы А:
- R1, Замена равных. Заменить один или больше экземпляры А в C от B, в результате чего E. Если А=B, тогда C=E.
- R2, Равномерная замена. Заменить все экземпляры А в C и D с участием B. C становится E и D становится F. Если C=D, тогда E=F. Обратите внимание, что А=B не требуется.
R2 очень часто используется в первичная алгебра демонстрации (см. ниже) почти всегда в тишине. Эти правила обычно используются в логика и большая часть математики, почти всегда бессознательно.
В первичная алгебра состоит из уравнения, т.е. пары формул, соединенных инфиксом '='. R1 и R2 позволяют преобразовывать одно уравнение в другое. Следовательно первичная алгебра является эквациональный формальная система, как и многие алгебраические структуры, в том числе Булева алгебра, которые разновидности. Раньше уравнительная логика была распространена Principia Mathematica (например, Пирс,1,2,3 Johnson 1892) и имеет современных защитников (Gries and Schneider 1993).
Обычный математическая логика состоит из тавтологический формулы, обозначенные префиксом турникет. Чтобы обозначить, что первичная алгебра формула А это тавтология просто напишите "А =![]() ". Если заменить '=' в R1 и R2 с двусмысленный, полученные правила выполняются в традиционной логике. Однако традиционная логика в основном полагается на правило modus ponens; таким образом, обычная логика понент. Эквационально-поненциальная дихотомия выделяет многое из того, что отличает математическую логику от остальной математики.
". Если заменить '=' в R1 и R2 с двусмысленный, полученные правила выполняются в традиционной логике. Однако традиционная логика в основном полагается на правило modus ponens; таким образом, обычная логика понент. Эквационально-поненциальная дихотомия выделяет многое из того, что отличает математическую логику от остальной математики.
Инициалы
An начальный это первичная алгебра уравнение, проверяемое процедура принятия решения и как таковой не ан аксиома. LoF кладет инициалы:
|
| = . |
Отсутствие чего-либо справа от "=" выше является преднамеренным.
|
| C | = |
| . |
J2 знакомый распределительный закон из сентенциальная логика и Булева алгебра.
Другой набор инициалов, более удобный для вычислений:
| А | = | А. |
|
| = | . |
| А |
| = | А |
| . |
Это благодаря C2 что первичная алгебра это решетка. Благодаря J1a, это дополненная решетка чья верхняя граница ![]() . От J0,
. От J0, ![]() - соответствующая нижняя граница и элемент идентичности. J0 также является алгебраической версией A2 и проясняет смысл, в котором
- соответствующая нижняя граница и элемент идентичности. J0 также является алгебраической версией A2 и проясняет смысл, в котором ![]() псевдонимы с пустой страницей.
псевдонимы с пустой страницей.
T13 в LoF обобщает C2 следующим образом. Любые первичная алгебра (или сентенциональная логика) формула B можно рассматривать как заказанное дерево с участием ветви. Потом:
T13: А подформула А можно копировать по желанию на любую глубину B больше, чем у А, так долго как А и его копия находятся в той же ветке B. Кроме того, учитывая несколько экземпляров А в той же ветке B, все экземпляры, кроме самых мелких, являются избыточными.
Хотя для доказательства T13 потребуется индукция, интуиция, лежащая в основе этого, должна быть ясна.
C2 или его эквивалент называется:
- «Поколение» в LoF;
- «Исключение» у Джонсона (1892);
- «Проникновение» в творчестве Уильяма Бриккена.
Возможно, это первый пример аксиомы или правила с силой C2 было «Правило (де) итерации», объединяющее T13 и AA = A, из К. С. Пирс с экзистенциальные графы.
LoF утверждает, что конкатенацию можно читать как поездка на работу и ассоциация по умолчанию и, следовательно, не нужно явно предполагать или демонстрировать. (Пирс сделал аналогичное утверждение о своем экзистенциальные графы.) Пусть точка будет временным обозначением для установления группировки. Эта конкатенация коммутирует и объединяется, чтобы продемонстрировать:
- Начальная AC.D=CD.A и последствия AA=А (Бирн, 1946). Этот результат верен для всех решетки, потому что AA=А является простым следствием закон поглощения, справедливое для всех решеток;
- Инициалы AC.D=AD.C и J0. поскольку J0 только для решеток с нижней границей, этот метод верен только для ограниченные решетки (которые включают первичная алгебра и 2). Коммутативность тривиальна; просто установите А=
 . Ассоциативность: AC.D = CA.D = CD.A = A.CD.
. Ассоциативность: AC.D = CA.D = CD.A = A.CD.
Продемонстрировав ассоциативность, точку можно отбросить.
Инициалы в Meguire (2011): AC.D=CD.A, называется B1; Би 2, J0 выше; B3, J1a выше; и B4, C2. По дизайну эти инициалы очень похожи на аксиомы для абелева группа, G1-G3 ниже.
Теория доказательств
В первичная алгебра содержит три вида доказанных утверждений:
- Следствие это первичная алгебра уравнение проверено демонстрация. Демонстрация состоит из последовательности шаги, каждый шаг оправдан первоначальными или ранее продемонстрированными последствиями.
- Теорема это заявление в метаязык проверено доказательство, то есть аргумент, сформулированный на метаязыке, который принимают обученные математики и логики.
- Начальная, определенный выше. Демонстрации и доказательства используют инициал как аксиому.
Различие между последствиями и теорема справедливо для всех формальных систем, включая математику и логику, но обычно не делается явным. Демонстрация или процедура принятия решения могут быть выполнены и проверены компьютером. В доказательство из теорема не может быть.
Позволять А и B быть первичная алгебра формулы. Демонстрация А=B может происходить двумя способами:
- Изменить А по шагам, пока B получается, или наоборот;
- Упростите оба
 и
и 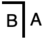 к
к  . Это известно как «расчет».
. Это известно как «расчет».
однажды А=B было продемонстрировано, А=B может использоваться для обоснования шагов в последующих демонстрациях. первичная алгебра для демонстраций и расчетов часто требуется не более J1a, J2, C2, и последствия ![]() (C3 в LoF),
(C3 в LoF), ![]() (C1), и AA=А (C5).
(C1), и AA=А (C5).
Следствие 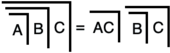 , C7 ' в LoF, позволяет алгоритм, нарисованный в LoFs доказательство T14, которое преобразует произвольный первичная алгебра формулу эквивалентной формулы, глубина которой не превышает двух. В результате нормальная форма, то первичная алгебра аналог конъюнктивная нормальная форма. LoF (T14–15) доказывает первичная алгебра аналог известного Булева алгебра Теорема о том, что каждая формула имеет нормальную форму.
, C7 ' в LoF, позволяет алгоритм, нарисованный в LoFs доказательство T14, которое преобразует произвольный первичная алгебра формулу эквивалентной формулы, глубина которой не превышает двух. В результате нормальная форма, то первичная алгебра аналог конъюнктивная нормальная форма. LoF (T14–15) доказывает первичная алгебра аналог известного Булева алгебра Теорема о том, что каждая формула имеет нормальную форму.
Позволять А быть подформула некоторых формула B. В паре с C3, J1a можно рассматривать как условие закрытия для расчетов: B это тавтология если и только если А и (А) оба появляются в глубине 0 B. Связанное условие появляется в некоторых версиях естественный вычет. Демонстрация расчетом часто немного больше, чем:
- Повторный вызов T13 для удаления повторяющихся подформул;
- Удаление любых подформул вида
 .
.
Последний шаг расчета всегда вызывает J1a.
LoF включает элегантные новые доказательства следующего стандарта метатеория:
- Полнота: все первичная алгебра последствия очевидны по инициалам (T17).
- Независимость: J1 не может быть продемонстрировано из J2 и наоборот (T18).
Это сентенциальная логика полностью преподается в каждом первом университетском курсе в математическая логика. Но университетские курсы по булевой алгебре редко упоминают полноту 2.
Интерпретации
Если состояния «Отмечено» и «Без пометки» читаются как Булево значения 1 и 0 (или Правда и Ложь), первичная алгебра интерпретирует 2 (или сентенциальная логика ). LoF показывает, как первичная алгебра может интерпретировать силлогизм. Каждый из них интерпретации обсуждается в подразделе ниже. Расширение первичная алгебра чтобы он мог интерпретировать стандарт логика первого порядка еще предстоит сделать, но Пирс с бета экзистенциальные графы предполагают, что это расширение возможно.
Двухэлементная булева алгебра 2
В первичная алгебра элегантное минималистское обозначение двухэлементная булева алгебра 2. Позволять:
- Один из булевых присоединиться (+) или встреча (×) интерпретировать конкатенация;
- В дополнять из А интерпретировать
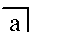
- 0 (1) интерпретировать пустую метку, если соединение (встреча) интерпретирует конкатенация (поскольку двоичная операция, применяемая к нулевым операндам, может рассматриваться как равная элемент идентичности этой операции; или, другими словами, отсутствующий операнд может рассматриваться как действующий по умолчанию как элемент идентичности).
Если присоединиться (встретиться) интерпретирует AC, затем встретить (присоединиться) интерпретирует . Следовательно первичная алгебра и 2 изоморфны, но с одной детали: первичная алгебра дополнение может быть нулевым, и в этом случае оно обозначает примитивное значение. По модулю этой детали, 2 это модель первичной алгебры. Первичная арифметика предполагает следующую арифметическую аксиоматизацию 2: 1 + 1 = 1 + 0 = 0 + 1 = 1 = ~ 0 и 0 + 0 = 0 = ~ 1.
В набор ![]()
![]() это Логический домен или перевозчик. На языке универсальная алгебра, то первичная алгебра это алгебраическая структура типа . В выразительная адекватность из Инсульт Шеффера указывает на первичная алгебра также будучи алгебра типа . В обоих случаях это тождества J1a, J0, C2 и ACD = CDA. Поскольку первичная алгебра и 2 находятся изоморфный, 2 можно рассматривать как алгебра типа . Это описание 2 проще обычного, а именно алгебра типа .
это Логический домен или перевозчик. На языке универсальная алгебра, то первичная алгебра это алгебраическая структура типа . В выразительная адекватность из Инсульт Шеффера указывает на первичная алгебра также будучи алгебра типа . В обоих случаях это тождества J1a, J0, C2 и ACD = CDA. Поскольку первичная алгебра и 2 находятся изоморфный, 2 можно рассматривать как алгебра типа . Это описание 2 проще обычного, а именно алгебра типа .
Две возможные интерпретации двойственны друг другу в булевом смысле. (В булевой алгебре замена AND ↔ OR и 1 ↔ 0 в уравнении дает одинаково допустимое уравнение.) Тождества остаются неизменными независимо от того, какая интерпретация выбрана, поэтому преобразования или режимы вычислений остаются теми же; только интерпретация каждой формы будет разной. Пример: J1a - это ![]() . Интерпретация сопоставления как ИЛИ и
. Интерпретация сопоставления как ИЛИ и ![]() как 1 это переводится как что является правдой. Интерпретация сопоставления как AND и
как 1 это переводится как что является правдой. Интерпретация сопоставления как AND и ![]() как 0 это переводится как что также верно (и двойственное ).
как 0 это переводится как что также верно (и двойственное ).
Предложения логика
Пусть пустая страница обозначает Ложь, и пусть крест читается как Не. Тогда первичная арифметика имеет следующий смысл:
- = Ложь
 = Правда = не ложь
= Правда = не ложь
 = Не правда = Ложь
= Не правда = Ложь
В первичная алгебра интерпретирует сентенциальную логику следующим образом. Буква представляет любое данное предложение. Таким образом:
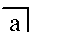 интерпретирует Не А
интерпретирует Не А
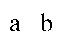 интерпретирует А или Б
интерпретирует А или Б
 интерпретирует Не А или Б или Если A, то B.
интерпретирует Не А или Б или Если A, то B.
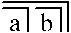 интерпретирует Нет (не A или не B)
интерпретирует Нет (не A или не B)- или Нет (если А, то не Б)
- или А и Б.
| , |
| оба интерпретируют А если и только если B или А это эквивалент в B. |
Таким образом, любое выражение в сентенциальная логика имеет первичная алгебра перевод. Эквивалентно первичная алгебра интерпретирует сентенциональная логика. Учитывая присвоение каждой переменной состояния Marked или Unmarked, это первичная алгебра перевод сводится к первичному арифметическому выражению, которое можно упростить. Повторение этого упражнения для всех возможных присвоений двух примитивных значений каждой переменной покажет, является ли исходное выражение тавтологический или удовлетворительный. Это пример процедура принятия решения, более или менее в духе обычных таблиц истинности. Учитывая некоторые первичная алгебра формула, содержащая N переменных, эта процедура принятия решения требует упрощения 2N первичные арифметические формулы. Для менее утомительной процедуры принятия решения больше в духе Куайн «анализ истинности», см. Meguire (2003).
Шварц (1981) доказал, что первичная алгебра эквивалентно - синтаксически, семантически, и теоретическое доказательство - с классическое исчисление высказываний. Таким же образом можно показать, что первичная алгебра синтаксически эквивалентен выражениям, построенным обычным образом из классического ценности истины правда и ложный, то логические связки НЕ, ИЛИ, И и круглые скобки.
Интерпретация немаркированного состояния как Ложь полностью произвольно; это состояние можно с равным успехом читать как Правда. Все, что требуется, - это интерпретация конкатенация изменить с OR на AND. IF A THEN B теперь переводится как ![]() вместо того
вместо того ![]() . В более общем плане первичная алгебра это "само-двойной ", что означает, что любой первичная алгебра формула имеет два приговор или Булево чтения, каждое двойной другого. Еще одно следствие самодуальности - нерелевантность Законы де Моргана; эти законы встроены в синтаксис первичная алгебра с самого начала.
. В более общем плане первичная алгебра это "само-двойной ", что означает, что любой первичная алгебра формула имеет два приговор или Булево чтения, каждое двойной другого. Еще одно следствие самодуальности - нерелевантность Законы де Моргана; эти законы встроены в синтаксис первичная алгебра с самого начала.
Истинный характер различия между первичная алгебра с одной стороны, и 2 а с другой стороны - логика высказываний. В последних формализмах дополнение /отрицание работа на «ничто» плохо сформирована. Но пустой Крест - это хорошо сформированный первичная алгебра выражение, обозначающее отмеченное состояние, примитивное значение. Следовательно, непустой Крест - это оператор, а пустой Крест - операнд потому что он обозначает примитивное значение. Таким образом первичная алгебра показывает, что прежде различные математические концепции оператора и операнда на самом деле представляют собой просто разные аспекты одного фундаментального действия, проведения различия.
Силлогизмы
Приложение 2 к LoF показывает, как переводить традиционный силлогизмы и сориты в первичная алгебра. Действительный силлогизм - это просто тот, чей первичная алгебра перевод упрощается до пустого Креста. Позволять А* обозначают буквальный, т.е. либо А или , равнодушно. Тогда каждый силлогизм, который не требует, чтобы один или несколько членов считались непустыми, является одной из 24 возможных перестановок обобщения Барбара чья первичная алгебра эквивалент . Эти 24 возможных перестановки включают 19 силлогистических форм, признанных действительными в Аристотелевский и средневековая логика. Эта первичная алгебра перевод силлогистической логики также предполагает, что первичная алгебра мочь интерпретировать монадический и термин логика, и что первичная алгебра имеет сходство с Схема логических терминов Куайна (1982: Часть II).
Пример расчета
Следующий расчет Лейбниц нетривиально Praeclarum Теорема иллюстрирует демонстративную силу первичная алгебра. Пусть C1 будет =А, C2 быть , C3 быть , J1a быть , и пусть OI означает, что переменные и подформулы были переупорядочены таким образом, чтобы это позволяли коммутативность и ассоциативность.
| [(п→р)∧(Q→S)]→[(п∧Q)→(р∧S)]. | Praeclarum Теорема. | ||||||||||||||||||||||
| первичная алгебра перевод | ||||||||||||||||||||||
| C1. | ||||||||||||||||||||||
| C1. | ||||||||||||||||||||||
| OI. | ||||||||||||||||||||||
| C2. | ||||||||||||||||||||||
| OI. | ||||||||||||||||||||||
| C2. | ||||||||||||||||||||||
| OI. | ||||||||||||||||||||||
| C2. | ||||||||||||||||||||||
| C1. | ||||||||||||||||||||||
| OI. | ||||||||||||||||||||||
| J1a. | ||||||||||||||||||||||
| OI. | ||||||||||||||||||||||
| C3. |
Отношение к магмам
В первичная алгебра воплощает точку зрения, отмеченную Хантингтон в 1933 г .: Булева алгебра требует, помимо одного унарная операция, один, а не два, бинарные операции. Отсюда редко упоминаемый факт, что булевы алгебры магмы. (Магмы назывались группоиды пока последний срок не был присвоен теория категорий.) Чтобы увидеть это, обратите внимание, что первичная алгебра это коммутативный:
- Полугруппа потому что первичная алгебра сопоставление ездит на работу и соратники;
- Моноид с участием элемент идентичности
 , благодаря J0.
, благодаря J0.
Группы также требуется унарная операция, называется обратный, групповой аналог Логическое дополнение. Позволять ![]() обозначим обратное к а. Позволять
обозначим обратное к а. Позволять ![]() обозначим группу элемент идентичности. Затем группы и первичная алгебра имеют те же подписи, а именно они оба алгебры типа 〈2,1,0〉. Следовательно первичная алгебра это граничная алгебра. Аксиомы для абелева группа, в граничных обозначениях:
обозначим группу элемент идентичности. Затем группы и первичная алгебра имеют те же подписи, а именно они оба алгебры типа 〈2,1,0〉. Следовательно первичная алгебра это граничная алгебра. Аксиомы для абелева группа, в граничных обозначениях:
- G1. abc = акб (предполагая ассоциацию слева);
- G2.
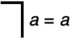
- G3.
 .
.
От G1 и G2, коммутативность и ассоциативность конкатенации могут быть получены, как указано выше. Обратите внимание, что G3 и J1a идентичны. G2 и J0 было бы идентично, если бы![]() =
= ![]() заменены A2. Это определяющее арифметическое тождество теории групп в граничных обозначениях.
заменены A2. Это определяющее арифметическое тождество теории групп в граничных обозначениях.
В первичная алгебра отличается от абелева группа двумя способами:
- От A2, это следует из того
 ≠
≠  . Если первичная алгебра были группа,
. Если первичная алгебра были группа,  =
=  будет держать, и один из
будет держать, и один из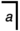 а =
а =  илиа
илиа  = а должен быть первичная алгебра следствие. Обратите внимание, что
= а должен быть первичная алгебра следствие. Обратите внимание, что  и
и  взаимны первичная алгебра дополняет, как того требует теория групп, так что верно как для теории групп, так и для первичная алгебра;
взаимны первичная алгебра дополняет, как того требует теория групп, так что верно как для теории групп, так и для первичная алгебра; - C2 наиболее четко разграничивает первичная алгебра из других магм, потому что C2 позволяет продемонстрировать закон поглощения что определяет решетки, а распределительный закон центральный для Булева алгебра.
И то и другое A2 и C2 следовать из B является заказанный набор.
Уравнения второй степени (Глава 11)
Глава 11 LoF вводит уравнения второй степени, состоящий из рекурсивный формулы, которые можно рассматривать как имеющие "бесконечную" глубину. Некоторые рекурсивные формулы упрощаются до отмеченного или немаркированного состояния. Другие неопределенно «колеблются» между двумя состояниями в зависимости от того, четная или нечетная заданная глубина. В частности, некоторые рекурсивные формулы можно интерпретировать как колебания между правда и ложный через последовательные интервалы времени, и в этом случае считается, что формула имеет «мнимое» значение истинности. Таким образом, поток времени может быть введен в первичная алгебра.
Терни (1986) показывает, как эти рекурсивные формулы можно интерпретировать с помощью Церковь Алонсо Ограниченная рекурсивная арифметика (RRA). Чёрч представил RRA в 1955 году как аксиоматическую формализацию конечные автоматы. Терни (1986) представляет общий метод перевода уравнений второй степени в RRA Черча, иллюстрируя его метод с помощью формул E1, E2, и E4 в главе 11 LoF. Этот перевод на RRA проливает свет на имена, которые Спенсер-Браун дал E1 и E4, а именно «память» и «счетчик». Таким образом, АРСП формализует и уточняет LoF понятие мнимой истинности ценности.
Связанных с работой
Готфрид Лейбниц в меморандумах, не опубликованных до конца 19 - начала 20 веков, изобрел Логическая логика. Его обозначения были изоморфны обозначениям LoF: конкатенация читается как соединение, и "не- (Икс) "читать как дополнять из Икс. Признание новаторской роли Лейбница в алгебраическая логика было предсказано Льюис (1918) и Решер (1954). Но полной оценки достижений Лейбница нужно было дождаться работы Вольфганга Ленцена, опубликованной в 1980-х годах и рассмотренной в Lenzen (2004).
Чарльз Сандерс Пирс (1839–1914) предвосхитили первичная алгебра в трех направлениях работы:
- В двух статьях, написанных им в 1886 году, была предложена логическая алгебра, в которой использовался только один символ - стример, почти идентичен Кресту LoF. Семантика стримера идентична семантике Креста, за исключением того, что Пирс никогда не писал стример без ничего под ним. Отрывок из одной из этих статей был опубликован в 1976 г.[7] но они не были опубликованы полностью до 1993 года.[8]
- В статье энциклопедии 1902 г.[9] Пирс обозначил булеву алгебру и сентенциональную логику в манере этой записи, за исключением того, что он использовал два стиля скобок, переключаясь между '(', ')' и '[', ']' с каждым приращением глубины формулы.
- В синтаксис его альфы экзистенциальные графы просто конкатенация, читать как соединение, а вложение овалами, читать как отрицание.[10] Если первичная алгебра конкатенация читается как соединение, то эти графики изоморфный к первичная алгебра (Кауфман 2001).
Как ни странно, LoF цитирует т. 4 Пирса Сборник статей, источник формализмов в (2) и (3) выше. (1) - (3) были практически неизвестны в то время, когда (1960-е) и в месте, где (Великобритания) LoF было написано. Пирса семиотика, о котором LoF молчит, но может пролить свет на философские аспекты LoF.
Кауфман (2001) обсуждает другие обозначения, аналогичные обозначениям LoF, что из статьи 1917 г. Жан Никод, который был учеником Бертран Рассел с.
Приведенные выше формализмы, как и первичная алгебра, все экземпляры граничная математика, то есть математика, синтаксис которой ограничен буквами и скобками (закрывающими элементами). Такой минималистский синтаксис - это «граничная нотация». Граничные обозначения свободны от инфикс, приставка, или постфикс символы операторов. Очень известные фигурные скобки ('{', '}') теории множеств можно рассматривать как граничные обозначения.
Работы Лейбница, Пирса и Никода не имеют отношения к метатеории, как они писали ранее. Эмиль Пост эпохальная газета 1920 г. ( LoF цитирует), доказывая, что сентенциальная логика завершено, и прежде Гильберта и Лукасевич показал, как доказать аксиома независимости с помощью модели.
Крейг (1979) утверждали, что мир и то, как люди воспринимают этот мир и взаимодействуют с ним, имеет богатую булеву структуру. Крейг был ортодоксальным логиком и авторитетом в алгебраическая логика.
Второе поколение наука о мышлении возникла в 1970-х, после LoF было написано. О когнитивной науке и ее значении для булевой алгебры, логики и теория множеств см. Lakoff (1987) (см. записи указателя в разделе «Примеры схем изображений: контейнер») и Lakoff and Núñez (2001). Ни одна из книг не цитирует LoF.
Биологи и когнитивисты Умберто Матурана и его ученик Франсиско Варела оба обсуждают LoF в своих трудах, которые определяют «различие» как фундаментальный познавательный акт. Психолог и когнитивист из Беркли Элеонора Рош много писал о тесно связанном понятии категоризации.
Другие формальные системы с возможным сродством к первичной алгебре включают:
- Мереология который обычно имеет решетка структура очень похожа на структуру булевой алгебры. Для некоторых авторов мереология - это просто модель из Булева алгебра а значит, и первичной алгебры.
- Мереотопология, которая по своей сути богаче булева алгебры;
- Система Уайтхеда (1934), фундаментальным примитивом которой является «индикация».
Первичная арифметика и алгебра - это минималистский формализм для сентенциальная логика и булева алгебра. Другие минималистические формализмы, обладающие силой теория множеств включают:
- В лямбда-исчисление;
- Комбинаторная логика с двумя (S и K) или даже один (Икс) примитивные комбинаторы;
- Математическая логика сделано с помощью всего трех примитивных понятий: одно связующее, NAND (чья первичная алгебра перевод или, вдвойне, ), универсальный количественная оценка, и один двоичный атомная формула, обозначая набор членство. Это система Куайн (1951).
- В бета экзистенциальные графы, с одним бинарный предикат обозначает членство в наборе. Это еще предстоит изучить. В альфа Упомянутые выше графики являются частным случаем бета графики.
Смотрите также
- Булева алгебра (Простая английская Википедия)
- Булева алгебра (введение)
- Булева алгебра (логика)
- Булева алгебра (структура)
- Канонически определенные булевы алгебры
- Логическая логика
- Энтуитивный граф
- Экзистенциальный граф
- Список тем по булевой алгебре
- Исчисление высказываний
- Двухэлементная булева алгебра
Заметки
- ^ Мегуайр, П. (2011) Граничная алгебра: более простой подход к базовой логике и булевой алгебре. Саарбрюккен: VDM Publishing Ltd. 168pp.
- ^ Шенвельдер-Кунце, Татьяна; Вилле, Катрин; Хёльшер, Томас; Спенсер Браун, Джордж (2009). "Джордж Спенсер Браун: Eine Einführung in die Законы формы, 2. Auflage ". Висбаден: VS Verlag für Sozialwissenschaften. ISBN 978-3-531-16105-1.
- ^ Феликс Лау: Die Form der Paradoxie, 2005 Карл-Ауэр Верлаг, ISBN 9783896703521
- ^ Мюллер, Альберт (2008). «Вычисление реальности. Лекция Хайнца фон Ферстера на конференции A.U.M в 1973 году» (PDF). Конструктивистские основы. 4 (1): 62–69.
- ^ Б. Банащевский (июль 1977 г.). "О законах формы Дж. Спенсера Брауна". Журнал формальной логики Нотр-Дам. 18 (3): 507–509. Дои:10.1305 / ndjfl / 1093888028.
- ^ Для сочувственной оценки см. Кауфман (2001).
- ^ "Качественная логика", MS 736 (около 1886 г.) в Eisele, Carolyn, ed. 1976 г. Новые элементы математики Чарльза С. Пирса. Vol. 4, математическая философия. (Гаага) Мутон: 101-15,1
- ^ «Качественная логика», MS 582 (1886) в Kloesel, Christian et al., Eds., 1993. Произведения Чарльза С. Пирса: хронологическое издание, Vol. 5, 1884–1886 гг.. Издательство Индианского университета: 323-71. «Логика родственников: качественные и количественные», MS 584 (1886) в Kloesel, Christian et al., Eds., 1993. Сочинения Чарльза С. Пирса: хронологическое издание, Vol. 5, 1884–1886 гг.. Издательство Индианского университета: 372-78.
- ^ Перепечатано в Peirce, C.S. (1933) Собрание статей Чарльза Сандерса Пирса, Vol. 4, Чарльз Хартсхорн и Пол Вайс, ред. Издательство Гарвардского университета. Пункты 378–383
- ^ Экзистенциальные графы подробно описаны в Peirce, C.S. (1933). Сборник статей. 4, Чарльз Хартсхорн и Пол Вайс, ред. Издательство Гарвардского университета. Пункты 347–529.
использованная литература
- Издания Законы формы:
- 1969. Лондон: Аллен и Анвин, твердый переплет.
- 1972. Crown Publishers, твердый переплет: ISBN 0-517-52776-6
- 1973. Bantam Books, мягкая обложка. ISBN 0-553-07782-1
- 1979. E.P. Даттон, мягкая обложка. ISBN 0-525-47544-3
- 1994. Портленд, штат Орегон: Компания Cognizer, мягкая обложка. ISBN 0-9639899-0-1
- 1997 немецкий перевод, озаглавленный Gesetze der Form. Любек: Bohmeier Verlag. ISBN 3-89094-321-7
- 2008 Bohmeier Verlag, Лейпциг, 5-е международное издание. ISBN 978-3-89094-580-4
- Босток, Дэвид, 1997. Промежуточная логика. Oxford Univ. Нажмите.
- Бирн, Ли, 1946, "Две формулировки булевой алгебры", Бюллетень Американского математического общества: 268–71.
- Крейг, Уильям (1979). «Булева логика и повседневный физический мир». Труды и адреса Американской философской ассоциации. 52 (6): 751–78. Дои:10.2307/3131383. JSTOR 3131383.
- Дэвид Грис, и Шнайдер, Ф. Б., 1993. Логический подход к дискретной математике. Springer-Verlag.
- Уильям Эрнест Джонсон, 1892, "Логическое исчисление", Разум 1 (н.у.): 3–30.
- Луи Х. Кауфман, 2001, "Математика К.С. Пирса ", Кибернетика и человеческое знание 8: 79–110.
- ------, 2006, "Переформулировка теоремы о цвете карты. "
- ------, 2006а. "Законы формы - исследование математики и основ. «Книжный черновик (отсюда большой).
- Ленцен, Вольфганг, 2004 г. "Логика Лейбница "в Gabbay, D., and Woods, J., eds., Расцвет современной логики: от Лейбница до Фреге (Справочник по истории логики - том 3). Амстердам: Elsevier, 1–83.
- Лакофф, Джордж, 1987. Женщины, огонь и опасные вещи. Издательство Чикагского университета.
- -------- и Рафаэль Э. Нуньес, 2001. Откуда пришла математика: Как воплощенный разум воплощает математику в жизнь. Основные книги.
- Мегуайр, П. Г. (2003). "Открытие граничной алгебры: упрощенное обозначение для булевой алгебры и функторов истины". Международный журнал общих систем. 32: 25–87. CiteSeerX 10.1.1.106.634. Дои:10.1080/0308107031000075690.
- --------, 2011. Граничная алгебра: более простой подход к базовой логике и булевой алгебре. ООО "ВДМ Паблишинг" ISBN 978-3639367492. Источник большей части этой записи, включая обозначения, заключенные в скобки, что LoF места под крест. Избегает более спекулятивных аспектов LoF.
- Уиллард Куайн, 1951. Математическая логика, 2-е изд. Издательство Гарвардского университета.
- --------, 1982. Методы логики, 4-е изд. Издательство Гарвардского университета.
- Решер, Николай (1954). "Интерпретация Лейбница его логических исчислений". Журнал символической логики. 18 (1): 1–13. Дои:10.2307/2267644. JSTOR 2267644.
- Шварц, Дэниел Г. (1981). «Изоморфизмы Г. Спенсера-Брауна Законы формы и Исчисление Ф. Варелы для самопроверки ». Международный журнал общих систем. 6 (4): 239–55. Дои:10.1080/03081078108934802.
- Терни, П. Д. (1986). "Законы формы и конечные автоматы ». Международный журнал общих систем. 12 (4): 307–18. Дои:10.1080/03081078608934939.
- А. Н. Уайтхед, 1934, «Показания, классы, номер, проверка», Разум 43 (n.s.): 281–97, 543. Исправления на стр. 543 являются многочисленными и важными, и более поздние перепечатки этой статьи не включают их.
- Дирк Беккер (редактор) (1993), Kalkül der Form. Зуркамп; Дирк Беккер (ред.), Probleme der Form. Suhrkamp.
- Дирк Беккер (редактор) (1999), Проблемы формы, Stanford University Press.
- Дирк Беккер (редактор) (2013), Математика формы, социология наблюдателей, Кибернетика и знание человека, т. 20, нет. 3-4.
внешние ссылки
- Законы формы, архив сайта Ричарда Шупа.
- Переговоры Спенсера-Брауна в Эсалене, 1973 г. Самореферентные формы вводятся в разделе «Степень уравнений и теория типов».
- Луи Х. Кауфман, "Бокс-алгебра, граничная математика, логика и законы формы. "
- Кисель, Матиас "Несистематическое, но легкое для понимания введение в Законы формы. "
- В Законы формы Forum, где первичная алгебра и связанные с ней формализмы обсуждаются с 2002 года.
- Встреча с G.S.B Моше Кляйн
- Отличительный знак, поэтапное введение в идеи Законы формы
- Исчисление BF и квадратный корень отрицания Луи Кауфман и Артур Коллингс; он расширяет законы формы, добавляя воображаемое логическое значение. (Мнимые логические значения представлены в главе 11 книги. Законы формы.)
- Курс законов формы - бесплатный он-лайн курс знакомит людей с основной частью текста «Законов формы» Леона Конрада, последнего ученика Спенсер-Брауна, который изучал работу с автором.

























