Усеченный икосаэдр - Truncated icosahedron
| Усеченный икосаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 32, E = 90, V = 60 (χ = 2) |
| Лица по сторонам | 12{5}+20{6} |
| Обозначение Конвея | tI |
| Символы Шлефли | т {3,5} |
| т0,1{3,5} | |
| Символ Wythoff | 2 5 | 3 |
| Диаграмма Кокстера | |
| Группа симметрии | ячас, H3, [5,3], (* 532), заказ 120 |
| Группа вращения | я, [5,3]+, (532), заказ 60 |
| Двугранный угол | 6-6: 138.189685° 6-5: 142.62° |
| Рекомендации | U25, C27, W9 |
| Характеристики | Полурегулярный выпуклый |
 Цветные лица |  5.6.6 (Фигура вершины ) |
 Додекаэдр пентакиса (двойственный многогранник ) |  Сеть |

В геометрия, то усеченный икосаэдр является Архимедово твердое тело, один из 13 выпуклых изогональный непризматические тела, 32 лица два или более типа правильные многоугольники.
Имеет 12 обычных пятиугольник лиц, 20 обычных шестиугольник граней, 60 вершин и 90 ребер.
Это Многогранник Гольдберга GPV(1,1) или {5 +, 3}1,1, содержащий пятиугольные и шестиугольные грани.
Эта геометрия связана с футбольные мячи (футбольные мячи) обычно украшены белыми шестиугольниками и черными пятиугольниками. Геодезические купола такие как те, чья архитектура Бакминстер Фуллер новаторские часто основываются на этой структуре. Это также соответствует геометрии фуллерена. C60 ("бакибол") молекула.
Он используется в клеточно-транзитивный гиперболическая тесселяция, заполняющая пространство, додекаэдрические соты с усеченным битом порядка 5.
Строительство
Этот многогранник можно построить из икосаэдр с 12 вершинами усеченный (отрезать) таким образом, чтобы отрезать по одной трети каждого края с каждого из концов. Это создает 12 новых граней пятиугольника, а исходные 20 граней треугольника остаются правильными шестиугольниками. Таким образом, длина краев составляет одну треть от длины исходных краев.
Характеристики
В Геометрия и Теория графов, есть стандартные характеристики многогранника.
Декартовы координаты
Декартовы координаты для вершин усеченный икосаэдр с центром в начале координат все даже перестановки из:
- (0, ±1, ±3φ)
- (±1, ±(2 + φ), ±2φ)
- (±φ, ±2, ±(2φ + 1))
куда φ = 1 + √5/2 это Золотая середина. Окружной радиус √9φ + 10 ≈ 4.956, а ребра имеют длину 2.[1]
Ортогональные проекции
В усеченный икосаэдр имеет пять специальных ортогональные проекции по центру на вершине, на двух типах ребер и двух типах граней: шестиугольной и пятиугольной. Последние два соответствуют букве A2 и H2 Самолеты Кокстера.
| В центре | Вершина | Край 5-6 | Край 6-6 | Лицо Шестиугольник | Лицо Пентагон |
|---|---|---|---|---|---|
| Твердый |  |  |  | ||
| Каркас |  | 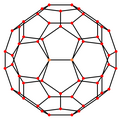 |  |  |  |
| Проективный симметрия | [2] | [2] | [2] | [6] | [10] |
| Двойной | 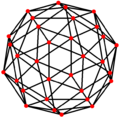 | 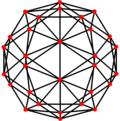 |  |  |  |
Сферическая черепица
Усеченный икосаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
 |  пятиугольник -центрированный |  шестиугольник -центрированный |
| Ортографическая проекция | Стереографические проекции | |
|---|---|---|
Размеры
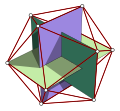
Если длина ребра усеченного икосаэдра равна а, то радиус из ограниченная сфера (тот, который касается усеченного икосаэдра во всех вершинах):
куда φ это Золотое сечение.
Этот результат легко получить, используя один из трех ортогональных золотые прямоугольники нарисованный в исходном икосаэдре (до отсечения) в качестве отправной точки для наших размышлений. Угол между сегментами, соединяющими центр, и вершинами, соединенными общим ребром (рассчитанный на основе этой конструкции), составляет примерно 23,281446 °.
Площадь и объем
Площадь А и объем V усеченного икосаэдра реберной длины а находятся:
С единичными краями площадь поверхности составляет (округленная) 21 для пятиугольника и 52 для шестиугольника, вместе 73 (см. площади правильных многоугольников ).
Усеченный икосаэдр легко демонстрирует Эйлерова характеристика:
- 32 + 60 − 90 = 2.
Приложения
Шары, используемые в ассоциация футбола и командный гандбол пожалуй, самый известный пример сферический многогранник аналог усеченного икосаэдра, встречающийся в повседневной жизни.[2] Мяч состоит из правильных пятиугольников и правильных шестиугольников, но он более сферический из-за давления воздуха внутри и эластичности шара. Этот тип мяча был представлен Чемпионат мира 1970 г. (начиная с 2006, этот знаковый дизайн был заменен альтернативные модели ).
Геодезические купола обычно основаны на треугольных гранях этой геометрии с примерами структур, найденных по всему миру, популяризированных Бакминстер Фуллер.[нужна цитата ]
Вариант икосаэдра был использован в качестве основы сотовых колес (изготовленных из поликарбоната). Подразделение Pontiac Motor с 1971 по 1976 год на его Trans Am и Гран При.[нужна цитата ]
Эта форма была также конфигурацией линз, используемых для фокусировки взрывных ударных волн детонаторов в обоих гаджет и Толстяк атомные бомбы.[3]
Усеченный икосаэдр также можно описать как модель Бакминстерфуллерен (фуллерен) (C60), или "бакибол", молекула - аллотроп элементарного углерода, открытый в 1985 году. Диаметр футбольного мяча и молекулы фуллерена составляет 22 см и около 0,71нм соответственно, поэтому соотношение размеров ≈31000000: 1.
В народной культуре ремесел большое искры можно сделать с помощью икосаэдр и пластиковые, пенопластовые или бумажные стаканчики.
В искусстве
- Галерея

Усеченный икосаэдр (слева) по сравнению с ассоциация футбола.

Фуллерен C60 молекула

Усеченный икосаэдр обтекатель на метеостанция

Усеченный икосаэдр, вырезанный из 6061-T6 алюминий

Деревянный усеченный икосаэдр. Джордж У. Харт.
Связанные многогранники
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| *п32 мутации симметрии усеченных мозаик: п.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п42 [n, 3] | Сферический | Евклид. | Компактный | Parac. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | ||
| Усеченный цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| н-кис цифры |  |  |  |  |  |  |  | |||||
| Конфиг. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Эти однородные звездные многогранники, а одна икосаэдрическая звездчатая имеет неоднородные усеченные икосаэдры выпуклые оболочки:
| Однородные звездчатые многогранники с выпуклой оболочкой усеченных икосаэдров | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Усеченный граф икосаэдра
| Усеченный икосаэдрический граф | |
|---|---|
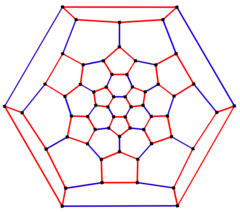 6-кратная симметрия диаграмма Шлегеля | |
| Вершины | 60 |
| Края | 90 |
| Автоморфизмы | 120 |
| Хроматическое число | 3 |
| Характеристики | Кубический, Гамильтониан, обычный, нулевой симметричный |
| Таблица графиков и параметров | |
в математический поле теория графов, а усеченный икосаэдрический граф это граф вершин и ребер из усеченный икосаэдр, один из Архимедовы тела. Имеет 60 вершины и 90 ребер, и является кубический Архимедов граф.[4][5][6][7]
 5-кратная симметрия | 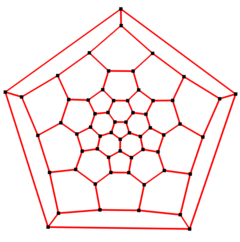 5-кратная диаграмма Шлегеля |
История

Усеченный икосаэдр был известен Архимед, который классифицировал 13 твердых тел Архимеда в утерянной работе. Все, что мы знаем о его работе над этими формами, исходит от Папп Александрийский, который просто перечисляет количество граней для каждой: 12 пятиугольников и 20 шестиугольников в случае усеченного икосаэдра. Первое известное изображение и полное описание усеченного икосаэдра получено при повторном открытии Пьеро делла Франческа, в его книге 15 века De quinque corporibus regularibus,[8] который включал пять архимедовых тел (пять усечений правильных многогранников). Такая же форма была изображена Леонардо да Винчи, в его иллюстрациях к Лука Пачоли плагиат книги делла Франческа в 1509 году. Альбрехт Дюрер исключил эту форму из других архимедовых тел, перечисленных в его книге 1525 года о многогранниках, Underweysung der Messung, описание его было найдено в его посмертных работах, опубликованных в 1538 году. Иоганн Кеплер позже заново открыл полный список из 13 архимедовых тел, включая усеченный икосаэдр, и включил их в свою книгу 1609 года, Harmonices Mundi.[9]
Смотрите также
Примечания
- ^ Вайсштейн, Эрик В. «Икосаэдрическая группа». MathWorld.
- ^ Кочик, Дитер (2006). «Топология и комбинаторика футбольных мячей». Американский ученый. 94 (4): 350–357. Дои:10.1511/2006.60.350.
- ^ Родос, Ричард (1996). Темное Солнце: Создание водородной бомбы. Книги оселка. стр.195. ISBN 0-684-82414-0.
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998). Атлас графиков. Oxford University Press. п. 268.
- ^ Вайсштейн, Эрик В. «Усеченный граф икосаэдра». MathWorld.
- ^ Годсил, К. и Ройл, Г. Алгебраическая теория графов Нью-Йорк: Springer-Verlag, стр. 211, 2001 г.
- ^ Костант, Б. График усеченного икосаэдра и последней буквы Галуа. Замечает амер. Математика. Soc. 42, 1995, стр. 959-968. PDF
- ^ Кац, Юджин А. (2011). «Мосты между математикой, естественными науками, архитектурой и искусством: случай фуллеренов». Искусство, наука и технологии: взаимодействие трех культур, Материалы Первой Международной конференции. С. 60–71.
- ^ Филд, Дж. (1997). «Повторное открытие архимедовых многогранников: Пьеро делла Франческа, Лука Пачоли, Леонардо да Винчи, Альбрехт Дюрер, Даниэле Барбаро и Иоганн Кеплер». Архив истории точных наук. 50 (3–4): 241–289. Дои:10.1007 / BF00374595 (неактивно 12.10.2020). JSTOR 41134110. МИСТЕР 1457069.CS1 maint: DOI неактивен по состоянию на октябрь 2020 г. (связь)
Рекомендации
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. (1997). «Архимедовы тела». Многогранники: «Одна из самых очаровательных глав геометрии». Кембридж: Издательство Кембриджского университета. С. 79–86. ISBN 0-521-55432-2. OCLC 180091468.
внешняя ссылка
- Эрик В. Вайсштейн, Усеченный икосаэдр (Архимедово твердое тело ) в MathWorld.
- Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3x5o - ti".
- Редактируемая сетка усеченного икосаэдра для печати с интерактивным трехмерным изображением
- Равномерные многогранники
- «Многогранники виртуальной реальности» —Энциклопедия многогранников
- 3D бумажная визуализация данных мяч чемпионата мира по футболу






























































