Кривые напряжение – деформация для различных моделей гиперупругих материалов.
А сверхупругий или Зеленая резинка материал[1] конститутивная модель в идеале эластичный материал, для которого зависимость напряжения от деформации определяется функция плотности энергии деформации . Гипеупругий материал - частный случай Эластичный материал Коши .
Для многих материалов линейная эластичность модели не точно описывают наблюдаемое поведение материала. Самый распространенный пример такого материала - резина, стресс -напряжение отношение можно определить как нелинейно-упругое, изотропный , несжимаемый и вообще не зависит от скорость деформации . Гиперупругость позволяет моделировать поведение таких материалов при напряжении и деформации.[2] вулканизированный эластомеры часто соответствует идеалу гиперупругости. Наполненные эластомеры и биологические ткани [3] [4]
Рональд Ривлин и Мелвин Муни разработаны первые гиперупругие модели, Неогукейский и Муни – Ривлин твердые тела. С тех пор было разработано много других гиперупругих моделей. Другие широко используемые модели гиперупругих материалов включают Огден модель и Модель Арруда – Бойса .
Модели гиперупругих материалов Модель Сен-Венана – Кирхгофа Простейшей моделью гиперупругого материала является модель Сен-Венана – Кирхгофа, которая представляет собой просто расширение геометрически линейной модели упругого материала до геометрически нелинейного режима. Эта модель имеет общий вид и изотропный вид соответственно.
S = C : E {displaystyle {oldsymbol {S}} = {oldsymbol {C}}: {oldsymbol {E}}} S = λ tr ( E ) я + 2 μ E . {displaystyle {oldsymbol {S}} = lambda ~ {ext {tr}} ({oldsymbol {E}}) {oldsymbol {mathit {I}}} + 2mu {oldsymbol {E}} {ext {.}}} где S {displaystyle {oldsymbol {S}}} C : я р 3 × 3 → я р 3 × 3 {displaystyle {oldsymbol {C}}: {m {I! R}} ^ {3 раза 3} ightarrow {m {I! R}} ^ {3 раза 3}} тензор жесткости и E {displaystyle {oldsymbol {E}}}
E = 1 2 [ ( ∇ Икс ты ) Т + ∇ Икс ты + ( ∇ Икс ты ) Т ⋅ ∇ Икс ты ] {displaystyle mathbf {E} = {frac {1} {2}} left [(abla _ {mathbf {X}} mathbf {u}) ^ {T} + abla _ {mathbf {X}} mathbf {u} + (abla _ {mathbf {X}} mathbf {u}) ^ {T} cdot abla _ {mathbf {X}} mathbf {u} ight] ,!} λ {displaystyle lambda} μ {displaystyle mu} Константы Ламе , и я {displaystyle {oldsymbol {mathit {I}}}}
Функция плотности энергии деформации для модели Сен-Венана – Кирхгофа имеет вид
W ( E ) = λ 2 [ tr ( E ) ] 2 + μ tr ( E 2 ) {displaystyle W ({oldsymbol {E}}) = {frac {lambda} {2}} [{ext {tr}} ({oldsymbol {E}})] ^ {2} + mu {ext {tr}} ( {oldsymbol {E}} ^ {2})} а второе напряжение Пиолы – Кирхгофа может быть получено из соотношения
S = ∂ W ∂ E . {displaystyle {oldsymbol {S}} = {cfrac {partial W} {partial {oldsymbol {E}}}} ~.} Классификация моделей гиперупругих материалов Модели гиперупругих материалов можно разделить на:
1) феноменологический описания наблюдаемого поведения
2) механистические модели вытекающие из аргументов о базовой структуре материала
3) гибриды феноменологической и механистической моделей
Как правило, гиперупругая модель должна удовлетворять Стабильность Друкера критерию. Некоторые гиперупругие модели удовлетворяют Гипотеза Валаниса-Ланделя который утверждает, что функцию энергии деформации можно разделить на сумму отдельных функций основные участки ( λ 1 , λ 2 , λ 3 ) {displaystyle (lambda _ {1}, lambda _ {2}, lambda _ {3})}
W = ж ( λ 1 ) + ж ( λ 2 ) + ж ( λ 3 ) . {displaystyle W = f (lambda _ {1}) + f (lambda _ {2}) + f (lambda _ {3}) ,.} Отношения напряжения и деформации Сжимаемые гиперупругие материалы Первое напряжение Пиолы – Кирхгофа Если W ( F ) {displaystyle W ({oldsymbol {F}})} 1-й тензор напряжений Пиолы – Кирхгофа можно рассчитать для гиперупругого материала как
п = ∂ W ∂ F или п я K = ∂ W ∂ F я K . {displaystyle {oldsymbol {P}} = {frac {partial W} {partial {oldsymbol {F}}}} qquad {ext {or}} qquad P_ {iK} = {frac {partial W} {partial F_ {iK}] }}.} где F {displaystyle {oldsymbol {F}}} градиент деформации . Что касается Лагранжева зеленая деформация ( E {displaystyle {oldsymbol {E}}}
п = F ⋅ ∂ W ∂ E или п я K = F я L ∂ W ∂ E L K . {displaystyle {oldsymbol {P}} = {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {E}}}}} qquad {ext {or}} qquad P_ {iK} = F_ {iL} ~ {frac {partial W} {partial E_ {LK}}} ~.} Что касается правый тензор деформации Коши – Грина ( C {displaystyle {oldsymbol {C}}}
п = 2 F ⋅ ∂ W ∂ C или п я K = 2 F я L ∂ W ∂ C L K . {displaystyle {oldsymbol {P}} = 2 ~ {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {C}}}} qquad {ext {or}} qquad P_ {iK} = 2 ~ F_ {iL} ~ {frac {partial W} {partial C_ {LK}}} ~.} Второе напряжение Пиолы – Кирхгофа Если S {displaystyle {oldsymbol {S}}} второй тензор напряжений Пиолы – Кирхгофа тогда
S = F − 1 ⋅ ∂ W ∂ F или S я J = F я k − 1 ∂ W ∂ F k J . {displaystyle {oldsymbol {S}} = {oldsymbol {F}} ^ {- 1} cdot {frac {partial W} {partial {oldsymbol {F}}}} qquad {ext {or}} qquad S_ {IJ} = F_ {Ik} ^ {- 1} {frac {partial W} {partial F_ {kJ}}} ~.} Что касается Лагранжева зеленая деформация
S = ∂ W ∂ E или S я J = ∂ W ∂ E я J . {displaystyle {oldsymbol {S}} = {frac {partial W} {partial {oldsymbol {E}}}} qquad {ext {or}} qquad S_ {IJ} = {frac {partial W} {partial E_ {IJ}} }} ~.} Что касается правый тензор деформации Коши – Грина
S = 2 ∂ W ∂ C или S я J = 2 ∂ W ∂ C я J . {displaystyle {oldsymbol {S}} = 2 ~ {frac {partial W} {partial {oldsymbol {C}}}} qquad {ext {or}} qquad S_ {IJ} = 2 ~ {frac {partial W} {partial C_ {IJ}}} ~.} Вышеупомянутое соотношение также известно как Формула Дойла-Эриксена в конфигурации материала.
Напряжение Коши Точно так же Напряжение Коши дан кем-то
σ = 1 J ∂ W ∂ F ⋅ F Т ; J := Det F или σ я j = 1 J ∂ W ∂ F я K F j K . {displaystyle {oldsymbol {sigma}} = {cfrac {1} {J}} ~ {cfrac {partial W} {partial {oldsymbol {F}}}} cdot {oldsymbol {F}} ^ {T} ~; ~~ J: = det {oldsymbol {F}} qquad {ext {or}} qquad sigma _ {ij} = {cfrac {1} {J}} ~ {cfrac {partial W} {partial F_ {iK}}} ~ F_ {jK} ~.} Что касается Лагранжева зеленая деформация
σ = 1 J F ⋅ ∂ W ∂ E ⋅ F Т или σ я j = 1 J F я K ∂ W ∂ E K L F j L . {displaystyle {oldsymbol {sigma}} = {cfrac {1} {J}} ~ {oldsymbol {F}} cdot {cfrac {partial W} {partial {oldsymbol {E}}}} cdot {oldsymbol {F}} ^ {T} qquad {ext {or}} qquad sigma _ {ij} = {cfrac {1} {J}} ~ F_ {iK} ~ {cfrac {partial W} {partial E_ {KL}}} ~ F_ {jL } ~.} Что касается правый тензор деформации Коши – Грина
σ = 2 J F ⋅ ∂ W ∂ C ⋅ F Т или σ я j = 2 J F я K ∂ W ∂ C K L F j L . {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ {oldsymbol {F}} cdot {cfrac {partial W} {partial {oldsymbol {C}}}} cdot {oldsymbol {F}} ^ {T} qquad {ext {or}} qquad sigma _ {ij} = {cfrac {2} {J}} ~ F_ {iK} ~ {cfrac {partial W} {partial C_ {KL}}} ~ F_ {jL } ~.} Приведенные выше выражения справедливы даже для анизотропных сред (в этом случае подразумевается, что потенциальная функция зависит от неявно от эталонных направленных величин, таких как начальная ориентация волокна). В частном случае изотропии напряжение Коши может быть выражено через осталось Тензор деформации Коши-Грина выглядит следующим образом:[5]
σ = 2 J B ⋅ ∂ W ∂ B или σ я j = 2 J B я k ∂ W ∂ B k j . {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ {oldsymbol {B}} cdot {cfrac {partial W} {partial {oldsymbol {B}}}} qquad {ext {or}} qquad sigma _ {ij} = {cfrac {2} {J}} ~ B_ {ik} ~ {cfrac {partial W} {partial B_ {kj}}} ~.} Несжимаемые гиперупругие материалы Для несжимаемый материал J := Det F = 1 {displaystyle J: = det {oldsymbol {F}} = 1} J − 1 = 0 {displaystyle J-1 = 0}
W = W ( F ) − п ( J − 1 ) {displaystyle W = W ({oldsymbol {F}}) - p ~ (J-1)} где гидростатическое давление п {displaystyle p} Множитель лагранжиана для обеспечения соблюдения ограничения несжимаемости. Первое напряжение Пиолы-Кирхгофа теперь становится
п = − п J F − Т + ∂ W ∂ F = − п F − Т + F ⋅ ∂ W ∂ E = − п F − Т + 2 F ⋅ ∂ W ∂ C . {displaystyle {oldsymbol {P}} = - p ~ J {oldsymbol {F}} ^ {- T} + {frac {partial W} {partial {oldsymbol {F}}}}} = - p ~ {oldsymbol {F} } ^ {- T} + {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {E}}}} = - p ~ {oldsymbol {F}} ^ {- T} + 2 ~ {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {C}}}} ~.} Этот тензор напряжений впоследствии может быть преобразованный в любой из других традиционных тензоров напряжений, таких как Тензор напряжений Коши который дается
σ = п ⋅ F Т = − п 1 + ∂ W ∂ F ⋅ F Т = − п 1 + F ⋅ ∂ W ∂ E ⋅ F Т = − п 1 + 2 F ⋅ ∂ W ∂ C ⋅ F Т . {displaystyle {oldsymbol {sigma}} = {oldsymbol {P}} cdot {oldsymbol {F}} ^ {T} = - p ~ {oldsymbol {mathit {1}}} + {frac {partial W} {partial {oldsymbol {F}}}} cdot {oldsymbol {F}} ^ {T} = - p ~ {oldsymbol {mathit {1}}} + {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {E }}}} cdot {oldsymbol {F}} ^ {T} = - p ~ {oldsymbol {mathit {1}}} + 2 ~ {oldsymbol {F}} cdot {frac {partial W} {partial {oldsymbol {C) }}}} cdot {oldsymbol {F}} ^ {T} ~.} Выражения для напряжения Коши Сжимаемые изотропные гиперупругие материалы Для изотропный сверхупругих материалов, напряжение Коши можно выразить через инварианты левый тензор деформации Коши – Грина (или правый тензор деформации Коши – Грина ). Если функция плотности энергии деформации является W ( F ) = W ^ ( я 1 , я 2 , я 3 ) = W ¯ ( я ¯ 1 , я ¯ 2 , J ) = W ~ ( λ 1 , λ 2 , λ 3 ) {displaystyle W ({oldsymbol {F}}) = {hat {W}} (I_ {1}, I_ {2}, I_ {3}) = {ar {W}} ({ar {I}} _ { 1}, {ar {I}} _ {2}, J) = {ilde {W}} (лямбда _ {1}, лямбда _ {2}, лямбда _ {3})}
σ = 2 я 3 [ ( ∂ W ^ ∂ я 1 + я 1 ∂ W ^ ∂ я 2 ) B − ∂ W ^ ∂ я 2 B ⋅ B ] + 2 я 3 ∂ W ^ ∂ я 3 1 = 2 J [ 1 J 2 / 3 ( ∂ W ¯ ∂ я ¯ 1 + я ¯ 1 ∂ W ¯ ∂ я ¯ 2 ) B − 1 J 4 / 3 ∂ W ¯ ∂ я ¯ 2 B ⋅ B ] + [ ∂ W ¯ ∂ J − 2 3 J ( я ¯ 1 ∂ W ¯ ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ¯ ∂ я ¯ 2 ) ] 1 = 2 J [ ( ∂ W ¯ ∂ я ¯ 1 + я ¯ 1 ∂ W ¯ ∂ я ¯ 2 ) B ¯ − ∂ W ¯ ∂ я ¯ 2 B ¯ ⋅ B ¯ ] + [ ∂ W ¯ ∂ J − 2 3 J ( я ¯ 1 ∂ W ¯ ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ¯ ∂ я ¯ 2 ) ] 1 = λ 1 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 1 п 1 ⊗ п 1 + λ 2 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 2 п 2 ⊗ п 2 + λ 3 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 3 п 3 ⊗ п 3 {displaystyle {egin {align} {oldsymbol {sigma}} & = {cfrac {2} {sqrt {I_ {3}}}} left [left ({cfrac {partial {hat {W}}} {partial I_ {1) }}} + I_ {1} ~ {cfrac {partial {hat {W}}} {partial I_ {2}}} ight) {oldsymbol {B}} - {cfrac {partial {hat {W}}} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] +2 {sqrt {I_ {3}}} ~ {cfrac {partial {hat {W}}} {partial I_ {3 }}} ~ {oldsymbol {mathit {1}}} & = {cfrac {2} {J}} left [{cfrac {1} {J ^ {2/3}}} left ({cfrac {partial {ar {W}}} {partial {ar {I}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I}} _ {2}}} ight) {oldsymbol {B}} - {cfrac {1} {J ^ {4/3}}} ~ {cfrac {partial {ar {W}}} {partial {ar {I}}) _ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] & qquad qquad + left [{cfrac {partial {ar {W}}} {partial J}} - {cfrac {2} {3J}} слева ({ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I} } _ {2} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ight) ight] ~ {oldsymbol {mathit {1}}} & = {cfrac {2} {J}} слева [left ({cfrac {partial {ar {W}}}} {partial {ar {I}} _ {1}}} + {ar {I} } _ {1} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ight) {ar {oldsymbol {B}}} - {cfrac {partial {ar { W}}} {partial {ar {I}} _ {2}}} ~ {ar {oldsymbol {B}}} cdot {ar {oldsymbol {B}}} ight] + left [{cfrac {partial {ar { W}}} {partial J}} - {cfrac {2} {3J}} left ({ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I}) } _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {частичный {ar {W}}} {частичный {ar {I}} _ {2}}} полет] ~ {oldsymbol {mathit {1}}} & = {cfrac {lambda _ {1}} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac {partial {ilde {W} }} {частичная лямбда _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + {cfrac {lambda _ {2}} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac {partial {ilde {W}}} {partial lambda _ {2}}} ~ mathbf {n} _ {2} otimes mathbf {n} _ {2} + {cfrac { lambda _ {3}} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac {partial {ilde {W}}} {partial lambda _ {3}}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} конец {выровнено}}} (См. Страницу на левый тензор деформации Коши – Грина для определения этих символов).
Доказательство 1: В второй тензор напряжений Пиолы – Кирхгофа для гиперупругого материала дается выражением S = 2 ∂ W ∂ C {displaystyle {oldsymbol {S}} = 2 ~ {cfrac {partial W} {partial {oldsymbol {C}}}}} где C = F Т ⋅ F {displaystyle {oldsymbol {C}} = {oldsymbol {F}} ^ {T} cdot {oldsymbol {F}}} правый тензор деформации Коши – Грина и F {displaystyle {oldsymbol {F}}} градиент деформации . В Напряжение Коши дан кем-то
σ = 1 J F ⋅ S ⋅ F Т = 2 J F ⋅ ∂ W ∂ C ⋅ F Т {displaystyle {oldsymbol {sigma}} = {cfrac {1} {J}} ~ {oldsymbol {F}} cdot {oldsymbol {S}} cdot {oldsymbol {F}} ^ {T} = {cfrac {2} { J}} ~ {oldsymbol {F}} cdot {cfrac {partial W} {partial {oldsymbol {C}}}} cdot {oldsymbol {F}} ^ {T}} где J = Det F {displaystyle J = det {oldsymbol {F}}} я 1 , я 2 , я 3 {displaystyle I_ {1}, I_ {2}, I_ {3}} C {displaystyle {oldsymbol {C}}}
∂ W ∂ C = ∂ W ∂ я 1 ∂ я 1 ∂ C + ∂ W ∂ я 2 ∂ я 2 ∂ C + ∂ W ∂ я 3 ∂ я 3 ∂ C . {displaystyle {cfrac {partial W} {partial {oldsymbol {C}}}}} = {cfrac {partial W} {partial I_ {1}}} ~ {cfrac {partial I_ {1}} {partial {oldsymbol {C} }}} + {cfrac {partial W} {partial I_ {2}}} ~ {cfrac {partial I_ {2}} {partial {oldsymbol {C}}}}} + {cfrac {partial W} {partial I_ {3 }}} ~ {cfrac {partial I_ {3}} {partial {oldsymbol {C}}}} ~.} В производные инвариантов симметричного тензора C {displaystyle {oldsymbol {C}}}
∂ я 1 ∂ C = 1 ; ∂ я 2 ∂ C = я 1 1 − C ; ∂ я 3 ∂ C = Det ( C ) C − 1 {displaystyle {frac {partial I_ {1}} {partial {oldsymbol {C}}}}} = {oldsymbol {mathit {1}}} ~; ~~ {frac {partial I_ {2}} {partial {oldsymbol {C} }}}} = I_ {1} ~ {oldsymbol {mathit {1}}} - {oldsymbol {C}} ~; ~~ {frac {partial I_ {3}} {partial {oldsymbol {C}}}} = det ({oldsymbol {C}}) ~ {oldsymbol {C}} ^ {- 1}} Следовательно, мы можем написать
∂ W ∂ C = ∂ W ∂ я 1 1 + ∂ W ∂ я 2 ( я 1 1 − F Т ⋅ F ) + ∂ W ∂ я 3 я 3 F − 1 ⋅ F − Т . {displaystyle {cfrac {partial W} {partial {oldsymbol {C}}}}} = {cfrac {partial W} {partial I_ {1}}} ~ {oldsymbol {mathit {1}}} + {cfrac {partial W} {частично I_ {2}}} ~ (I_ {1} ~ {oldsymbol {mathit {1}}} - {oldsymbol {F}} ^ {T} cdot {oldsymbol {F}}) + {cfrac {частично W} {partial I_ {3}}} ~ I_ {3} ~ {oldsymbol {F}} ^ {- 1} cdot {oldsymbol {F}} ^ {- T} ~.} Подстановка выражения для напряжения Коши дает
σ = 2 J [ ∂ W ∂ я 1 F ⋅ F Т + ∂ W ∂ я 2 ( я 1 F ⋅ F Т − F ⋅ F Т ⋅ F ⋅ F Т ) + ∂ W ∂ я 3 я 3 1 ] {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ left [{cfrac {partial W} {partial I_ {1}}}} ~ {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T} + {cfrac {partial W} {partial I_ {2}}} ~ (I_ {1} ~ {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T} - {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T} cdot {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T}) + {cfrac {partial W} {partial I_ {3}}} ~ I_ {3} ~ {oldsymbol {mathit {1}}} ight]} С использованием левый тензор деформации Коши – Грина B = F ⋅ F Т {displaystyle {oldsymbol {B}} = {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T}} я 3 = J 2 {displaystyle I_ {3} = J ^ {2}}
σ = 2 я 3 [ ( ∂ W ∂ я 1 + я 1 ∂ W ∂ я 2 ) B − ∂ W ∂ я 2 B ⋅ B ] + 2 я 3 ∂ W ∂ я 3 1 . {displaystyle {oldsymbol {sigma}} = {cfrac {2} {sqrt {I_ {3}}}} ~ left [left ({cfrac {partial W} {partial I_ {1}}} + I_ {1} ~ { cfrac {partial W} {partial I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B} } ight] + 2 ~ {sqrt {I_ {3}}} ~ {cfrac {partial W} {partial I_ {3}}} ~ {oldsymbol {mathit {1}}} ~.} Для несжимаемый материал я 3 = 1 {displaystyle I_ {3} = 1} W = W ( я 1 , я 2 ) {displaystyle W = W (I_ {1}, I_ {2})}
∂ W ∂ C = ∂ W ∂ я 1 ∂ я 1 ∂ C + ∂ W ∂ я 2 ∂ я 2 ∂ C = ∂ W ∂ я 1 1 + ∂ W ∂ я 2 ( я 1 1 − F Т ⋅ F ) {displaystyle {cfrac {partial W} {partial {oldsymbol {C}}}}} = {cfrac {partial W} {partial I_ {1}}} ~ {cfrac {partial I_ {1}} {partial {oldsymbol {C} }}} + {cfrac {partial W} {partial I_ {2}}} ~ {cfrac {partial I_ {2}} {partial {oldsymbol {C}}}}} = {cfrac {partial W} {partial I_ {1 }}} ~ {oldsymbol {mathit {1}}} + {cfrac {partial W} {partial I_ {2}}} ~ (I_ {1} ~ {oldsymbol {mathit {1}}} - {oldsymbol {F}) } ^ {T} cdot {oldsymbol {F}})} Следовательно, напряжение Коши определяется выражением
σ = 2 [ ( ∂ W ∂ я 1 + я 1 ∂ W ∂ я 2 ) B − ∂ W ∂ я 2 B ⋅ B ] − п 1 . {displaystyle {oldsymbol {sigma}} = 2left [left ({cfrac {частичный W} {частичный I_ {1}}} + I_ {1} ~ {cfrac {partial W} {частичный I_ {2}}} полет) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] -p ~ {oldsymbol {mathit {1}}} ~ .} где п {displaystyle p} Множитель Лагранжа для обеспечения соблюдения ограничения несжимаемости.
Если, кроме того, я 1 = я 2 {displaystyle I_ {1} = I_ {2}} W = W ( я 1 ) {displaystyle W = W (I_ {1})}
∂ W ∂ C = ∂ W ∂ я 1 ∂ я 1 ∂ C = ∂ W ∂ я 1 1 {displaystyle {cfrac {partial W} {partial {oldsymbol {C}}}}} = {cfrac {partial W} {partial I_ {1}}} ~ {cfrac {partial I_ {1}} {partial {oldsymbol {C} }}} = {cfrac {partial W} {partial I_ {1}}} ~ {oldsymbol {mathit {1}}}} В этом случае напряжение Коши можно выразить как
σ = 2 ∂ W ∂ я 1 B − п 1 . {displaystyle {oldsymbol {sigma}} = 2 {cfrac {partial W} {partial I_ {1}}} ~ {oldsymbol {B}} - p ~ {oldsymbol {mathit {1}}} ~.}
Доказательство 2: В изохорный градиент деформации определяется как F ¯ := J − 1 / 3 F {displaystyle {ar {oldsymbol {F}}}: = J ^ {- 1/3} {oldsymbol {F}}} B ¯ := F ¯ ⋅ F ¯ Т = J − 2 / 3 B {displaystyle {ar {oldsymbol {B}}}: = {ar {oldsymbol {F}}} cdot {ar {oldsymbol {F}}} ^ {T} = J ^ {- 2/3} {oldsymbol {B}) }} Инварианты B ¯ {displaystyle {ar {oldsymbol {B}}}} я ¯ 1 = tr ( B ¯ ) = J − 2 / 3 tr ( B ) = J − 2 / 3 я 1 я ¯ 2 = 1 2 ( tr ( B ¯ ) 2 − tr ( B ¯ 2 ) ) = 1 2 ( ( J − 2 / 3 tr ( B ) ) 2 − tr ( J − 4 / 3 B 2 ) ) = J − 4 / 3 я 2 я ¯ 3 = Det ( B ¯ ) = J − 6 / 3 Det ( B ) = J − 2 я 3 = J − 2 J 2 = 1 {displaystyle {egin {align} {ar {I}} _ {1} & = {ext {tr}} ({ar {oldsymbol {B}}}) = J ^ {- 2/3} {ext {tr} } ({oldsymbol {B}}) = J ^ {- 2/3} I_ {1} {ar {I}} _ {2} & = {frac {1} {2}} left ({ext {tr }} ({ar {oldsymbol {B}}}) ^ {2} - {ext {tr}} ({ar {oldsymbol {B}}} ^ {2}) ight) = {frac {1} {2} } left (left (J ^ {- 2/3} {ext {tr}} ({oldsymbol {B}}) ight) ^ {2} - {ext {tr}} (J ^ {- 4/3} { oldsymbol {B}} ^ {2}) ight) = J ^ {- 4/3} I_ {2} {ar {I}} _ {3} & = det ({ar {oldsymbol {B}}}) = J ^ {- 6/3} det ({oldsymbol {B}}) = J ^ {- 2} I_ {3} = J ^ {- 2} J ^ {2} = 1end {выровнено}}} J {displaystyle J}
Чтобы выразить напряжение Коши через инварианты я ¯ 1 , я ¯ 2 , J {displaystyle {ar {I}} _ {1}, {ar {I}} _ {2}, J}
я ¯ 1 = J − 2 / 3 я 1 = я 3 − 1 / 3 я 1 ; я ¯ 2 = J − 4 / 3 я 2 = я 3 − 2 / 3 я 2 ; J = я 3 1 / 2 . {displaystyle {ar {I}} _ {1} = J ^ {- 2/3} ~ I_ {1} = I_ {3} ^ {- 1/3} ~ I_ {1} ~; ~~ {ar { I}} _ {2} = J ^ {- 4/3} ~ I_ {2} = I_ {3} ^ {- 2/3} ~ I_ {2} ~; ~~ J = I_ {3} ^ { 1/2} ~.} Цепное правило дифференциации дает нам
∂ W ∂ я 1 = ∂ W ∂ я ¯ 1 ∂ я ¯ 1 ∂ я 1 + ∂ W ∂ я ¯ 2 ∂ я ¯ 2 ∂ я 1 + ∂ W ∂ J ∂ J ∂ я 1 = я 3 − 1 / 3 ∂ W ∂ я ¯ 1 = J − 2 / 3 ∂ W ∂ я ¯ 1 ∂ W ∂ я 2 = ∂ W ∂ я ¯ 1 ∂ я ¯ 1 ∂ я 2 + ∂ W ∂ я ¯ 2 ∂ я ¯ 2 ∂ я 2 + ∂ W ∂ J ∂ J ∂ я 2 = я 3 − 2 / 3 ∂ W ∂ я ¯ 2 = J − 4 / 3 ∂ W ∂ я ¯ 2 ∂ W ∂ я 3 = ∂ W ∂ я ¯ 1 ∂ я ¯ 1 ∂ я 3 + ∂ W ∂ я ¯ 2 ∂ я ¯ 2 ∂ я 3 + ∂ W ∂ J ∂ J ∂ я 3 = − 1 3 я 3 − 4 / 3 я 1 ∂ W ∂ я ¯ 1 − 2 3 я 3 − 5 / 3 я 2 ∂ W ∂ я ¯ 2 + 1 2 я 3 − 1 / 2 ∂ W ∂ J = − 1 3 J − 8 / 3 J 2 / 3 я ¯ 1 ∂ W ∂ я ¯ 1 − 2 3 J − 10 / 3 J 4 / 3 я ¯ 2 ∂ W ∂ я ¯ 2 + 1 2 J − 1 ∂ W ∂ J = − 1 3 J − 2 ( я ¯ 1 ∂ W ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ∂ я ¯ 2 ) + 1 2 J − 1 ∂ W ∂ J {displaystyle {egin {align} {cfrac {partial W} {partial I_ {1}}}} & = {cfrac {partial W} {partial {ar {I}} _ {1}}} ~ {cfrac {partial {ar {I}} _ {1}} {partial I_ {1}}} + {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {cfrac {partial {ar {I}}} _ {2}} {частичный I_ {1}}} + {cfrac {частичный W} {частичный J}} ~ {cfrac {частичный J} {частичный I_ {1}}} & = I_ {3} ^ {- 1 / 3} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} = J ^ {- 2/3} ~ {cfrac {partial W} {partial {ar {I}} _ { 1}}} {cfrac {partial W} {partial I_ {2}}} & = {cfrac {partial W} {partial {ar {I}} _ {1}}} ~ {cfrac {partial {ar {I} }} _ {1}} {partial I_ {2}}} + {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {cfrac {partial {ar {I}}} _ {2 }} {частичный I_ {2}}} + {cfrac {частичный W} {частичный J}} ~ {cfrac {частичный J} {частичный I_ {2}}} & = I_ {3} ^ {- 2/3 } ~ {cfrac {частичный W} {частичный {ar {I}} _ {2}}} = J ^ {- 4/3} ~ {cfrac {частичный W} {частичный {ar {I}} _ {2} }} {cfrac {partial W} {partial I_ {3}}} & = {cfrac {partial W} {partial {ar {I}} _ {1}}} ~ {cfrac {partial {ar {I}} _ {1}} {partial I_ {3}}} + {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {cfrac {partial { ar {I}} _ {2}} {частичный I_ {3}}} + {cfrac {частичный W} {частичный J}} ~ {cfrac {частичный J} {частичный I_ {3}}} & = - { cfrac {1} {3}} ~ I_ {3} ^ {- 4/3} ~ I_ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} - {cfrac { 2} {3}} ~ I_ {3} ^ {- 5/3} ~ I_ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} + {cfrac {1} {2}} ~ I_ {3} ^ {- 1/2} ~ {cfrac {partial W} {partial J}} & = - {cfrac {1} {3}} ~ J ^ {- 8/3} ~ J ^ {2/3} ~ {ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} - {cfrac {2} {3}} ~ J ^ {- 10/3} ~ J ^ {4/3} ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} + {cfrac {1} {2}} ~ J ^ {- 1} ~ {cfrac {partial W} {partial J}} & = - {cfrac {1} {3}} ~ J ^ {- 2} ~ left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) + {cfrac {1} {2}} ~ J ^ {- 1} ~ {cfrac {partial W} {partial J}} end {выровнено }}} Напомним, что напряжение Коши определяется выражением
σ = 2 я 3 [ ( ∂ W ∂ я 1 + я 1 ∂ W ∂ я 2 ) B − ∂ W ∂ я 2 B ⋅ B ] + 2 я 3 ∂ W ∂ я 3 1 . {displaystyle {oldsymbol {sigma}} = {cfrac {2} {sqrt {I_ {3}}}} ~ left [left ({cfrac {partial W} {partial I_ {1}}} + I_ {1} ~ { cfrac {partial W} {partial I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B} } ight] + 2 ~ {sqrt {I_ {3}}} ~ {cfrac {partial W} {partial I_ {3}}} ~ {oldsymbol {mathit {1}}} ~.} В терминах инвариантов я ¯ 1 , я ¯ 2 , J {displaystyle {ar {I}} _ {1}, {ar {I}} _ {2}, J}
σ = 2 J [ ( ∂ W ∂ я 1 + J 2 / 3 я ¯ 1 ∂ W ∂ я 2 ) B − ∂ W ∂ я 2 B ⋅ B ] + 2 J ∂ W ∂ я 3 1 . {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ left [left ({cfrac {partial W} {partial I_ {1}}}} + J ^ {2/3} ~ {ar {I) }} _ {1} ~ {cfrac {partial W} {partial I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B }} cdot {oldsymbol {B}} ight] + 2 ~ J ~ {cfrac {partial W} {partial I_ {3}}} ~ {oldsymbol {mathit {1}}} ~.} Подставляя выражения для производных от W {displaystyle W} я ¯ 1 , я ¯ 2 , J {displaystyle {ar {I}} _ {1}, {ar {I}} _ {2}, J}
σ = 2 J [ ( J − 2 / 3 ∂ W ∂ я ¯ 1 + J − 2 / 3 я ¯ 1 ∂ W ∂ я ¯ 2 ) B − J − 4 / 3 ∂ W ∂ я ¯ 2 B ⋅ B ] + 2 J [ − 1 3 J − 2 ( я ¯ 1 ∂ W ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ∂ я ¯ 2 ) + 1 2 J − 1 ∂ W ∂ J ] 1 {displaystyle {egin {align} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [left (J ^ {- 2/3} ~ {cfrac {partial W}} {partial {ar {I }} _ {1}}} + J ^ {- 2/3} ~ {ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} полет ) ~ {oldsymbol {B}} - J ^ {- 4/3} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B }} ight] + & qquad 2 ~ J ~ left [- {cfrac {1} {3}} ~ J ^ {- 2} ~ left ({ar {I}} _ {1} ~ {cfrac {частичное W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {частичный {ar {I}} _ {2}}} полет) + {cfrac {1} {2}} ~ J ^ {- 1} ~ {cfrac {partial W} {partial J}} ight] ~ {oldsymbol {mathit {1}}} конец {выровнено}}} или,
σ = 2 J [ 1 J 2 / 3 ( ∂ W ∂ я ¯ 1 + я ¯ 1 ∂ W ∂ я ¯ 2 ) B − 1 J 4 / 3 ∂ W ∂ я ¯ 2 B ⋅ B ] + [ ∂ W ∂ J − 2 3 J ( я ¯ 1 ∂ W ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ∂ я ¯ 2 ) ] 1 {displaystyle {egin {align} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [{cfrac {1} {J ^ {2/3}}}} ~ left ({cfrac {partial W } {partial {ar {I}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial W} {частичный {ar {I}} _ {2}}} полёт) ~ {oldsymbol {B}} - {cfrac {1} {J ^ {4/3}}} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] & qquad + left [{cfrac {partial W} {partial J}} - {cfrac {2} {3J}} left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2} }} ight) ight] {oldsymbol {mathit {1}}} конец {выровнено}}} Что касается девиаторной части B {displaystyle {oldsymbol {B}}}
σ = 2 J [ ( ∂ W ∂ я ¯ 1 + я ¯ 1 ∂ W ∂ я ¯ 2 ) B ¯ − ∂ W ∂ я ¯ 2 B ¯ ⋅ B ¯ ] + [ ∂ W ∂ J − 2 3 J ( я ¯ 1 ∂ W ∂ я ¯ 1 + 2 я ¯ 2 ∂ W ∂ я ¯ 2 ) ] 1 {displaystyle {egin {align} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [left ({cfrac {partial W} {partial {ar {I}}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ~ {ar {oldsymbol {B}}} - {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {oldsymbol {B}}} cdot {ar {oldsymbol {B}}} ight] & qquad + left [{cfrac {partial W} {partial J }} - {cfrac {2} {3J}} left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ight] {oldsymbol {mathit {1}}} конец {выровнено}}} Для несжимаемый материал J = 1 {displaystyle J = 1} W = W ( я ¯ 1 , я ¯ 2 ) {displaystyle W = W ({ar {I}} _ {1}, {ar {I}} _ {2})}
σ = 2 [ ( ∂ W ∂ я ¯ 1 + я 1 ∂ W ∂ я ¯ 2 ) B ¯ − ∂ W ∂ я ¯ 2 B ¯ ⋅ B ¯ ] − п 1 . {displaystyle {oldsymbol {sigma}} = 2left [left ({cfrac {partial W} {partial {ar {I}} _ {1}}}} + I_ {1} ~ {cfrac {partial W}} {partial {ar { I}} _ {2}}} ight) ~ {ar {oldsymbol {B}}} - {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {oldsymbol {B} }} cdot {ar {oldsymbol {B}}} ight] -p ~ {oldsymbol {mathit {1}}} ~.} где п {displaystyle p} я ¯ 1 = я ¯ 2 {displaystyle {ar {I}} _ {1} = {ar {I}} _ {2}} W = W ( я ¯ 1 ) {displaystyle W = W ({ar {I}} _ {1})}
σ = 2 ∂ W ∂ я ¯ 1 B ¯ − п 1 . {displaystyle {oldsymbol {sigma}} = 2 {cfrac {partial W} {partial {ar {I}} _ {1}}} ~ {ar {oldsymbol {B}}} - p ~ {oldsymbol {mathit {1} }} ~.}
Доказательство 3: Чтобы выразить напряжение Коши через тянется λ 1 , λ 2 , λ 3 {displaystyle lambda _ {1}, lambda _ {2}, lambda _ {3}} ∂ λ я ∂ C = 1 2 λ я р Т ⋅ ( п я ⊗ п я ) ⋅ р ; я = 1 , 2 , 3 . {displaystyle {cfrac {partial lambda _ {i}} {partial {oldsymbol {C}}}}} = {cfrac {1} {2lambda _ {i}}} ~ {oldsymbol {R}} ^ {T} cdot (mathbf {n} _ {i} otimes mathbf {n} _ {i}) cdot {oldsymbol {R}} ~; ~~ i = 1,2,3 ~.} Цепное правило дает
∂ W ∂ C = ∂ W ∂ λ 1 ∂ λ 1 ∂ C + ∂ W ∂ λ 2 ∂ λ 2 ∂ C + ∂ W ∂ λ 3 ∂ λ 3 ∂ C = р Т ⋅ [ 1 2 λ 1 ∂ W ∂ λ 1 п 1 ⊗ п 1 + 1 2 λ 2 ∂ W ∂ λ 2 п 2 ⊗ п 2 + 1 2 λ 3 ∂ W ∂ λ 3 п 3 ⊗ п 3 ] ⋅ р {displaystyle {egin {align} {cfrac {partial W} {partial {oldsymbol {C}}}}} & = {cfrac {partial W} {partial lambda _ {1}}} ~ {cfrac {partial lambda _ {1} } {partial {oldsymbol {C}}}} + {cfrac {partial W} {partial lambda _ {2}}} ~ {cfrac {partial lambda _ {2}} {partial {oldsymbol {C}}}} + { cfrac {partial W} {partial lambda _ {3}}} ~ {cfrac {partial lambda _ {3}} {partial {oldsymbol {C}}}}} & = {oldsymbol {R}} ^ {T} cdot left [{cfrac {1} {2lambda _ {1}}} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + { cfrac {1} {2lambda _ {2}}} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ mathbf {n} _ {2} otimes mathbf {n} _ {2} + {cfrac { 1} {2lambda _ {3}}} ~ {cfrac {partial W} {partial lambda _ {3}}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} ight] cdot {oldsymbol { R}} конец {выровнен}}} Напряжение Коши определяется выражением
σ = 2 J F ⋅ ∂ W ∂ C ⋅ F Т = 2 J ( V ⋅ р ) ⋅ ∂ W ∂ C ⋅ ( р Т ⋅ V ) {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ {oldsymbol {F}} cdot {cfrac {partial W} {partial {oldsymbol {C}}}} cdot {oldsymbol {F}} ^ {T} = {cfrac {2} {J}} ~ ({oldsymbol {V}} cdot {oldsymbol {R}}) cdot {cfrac {partial W} {partial {oldsymbol {C}}}} cdot ({oldsymbol {R}} ^ {T} cdot {oldsymbol {V}})} Подставляя выражение для производной от W {displaystyle W}
σ = 2 J V ⋅ [ 1 2 λ 1 ∂ W ∂ λ 1 п 1 ⊗ п 1 + 1 2 λ 2 ∂ W ∂ λ 2 п 2 ⊗ п 2 + 1 2 λ 3 ∂ W ∂ λ 3 п 3 ⊗ п 3 ] ⋅ V {displaystyle {oldsymbol {sigma}} = {cfrac {2} {J}} ~ {oldsymbol {V}} cdot left [{cfrac {1} {2lambda _ {1}}} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + {cfrac {1} {2lambda _ {2}}} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ mathbf {n} _ {2} otimes mathbf {n} _ {2} + {cfrac {1} {2lambda _ {3}}} ~ {cfrac {partial W} {partial lambda _ {3 }}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} ight] cdot {oldsymbol {V}}} С использованием спектральное разложение из V {displaystyle {oldsymbol {V}}}
V ⋅ ( п я ⊗ п я ) ⋅ V = λ я 2 п я ⊗ п я ; я = 1 , 2 , 3. {displaystyle {oldsymbol {V}} cdot (mathbf {n} _ {i} otimes mathbf {n} _ {i}) cdot {oldsymbol {V}} = lambda _ {i} ^ {2} ~ mathbf {n} _ {i} otimes mathbf {n} _ {i} ~; ~~ i = 1,2,3.} Также обратите внимание, что
J = Det ( F ) = Det ( V ) Det ( р ) = Det ( V ) = λ 1 λ 2 λ 3 . {displaystyle J = det ({oldsymbol {F}}) = det ({oldsymbol {V}}) det ({oldsymbol {R}}) = det ({oldsymbol {V}}) = lambda _ {1} lambda _ {2} лямбда _ {3} ~.} Следовательно, выражение для напряжения Коши можно записать как
σ = 1 λ 1 λ 2 λ 3 [ λ 1 ∂ W ∂ λ 1 п 1 ⊗ п 1 + λ 2 ∂ W ∂ λ 2 п 2 ⊗ п 2 + λ 3 ∂ W ∂ λ 3 п 3 ⊗ п 3 ] {displaystyle {oldsymbol {sigma}} = {cfrac {1} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ left [lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ mathbf {n } _ {2} otimes mathbf {n} _ {2} + lambda _ {3} ~ {cfrac {partial W} {partial lambda _ {3}}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} ight]} Для несжимаемый материал λ 1 λ 2 λ 3 = 1 {displaystyle lambda _ {1} lambda _ {2} lambda _ {3} = 1} W = W ( λ 1 , λ 2 ) {displaystyle W = W (лямбда _ {1}, лямбда _ {2})} [1]
σ = λ 1 ∂ W ∂ λ 1 п 1 ⊗ п 1 + λ 2 ∂ W ∂ λ 2 п 2 ⊗ п 2 + λ 3 ∂ W ∂ λ 3 п 3 ⊗ п 3 − п 1 {displaystyle {oldsymbol {sigma}} = lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ mathbf {n} _ {2} otimes mathbf {n} _ {2} + lambda _ {3} ~ {cfrac {partial W } {частичная лямбда _ {3}}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} -p ~ {oldsymbol {mathit {1}}} ~} На этом этапе требуется некоторая осторожность, потому что, когда собственное значение повторяется, оно обычно Гато дифференцируемые , но нет Дифференцируемый по Фреше .[6] [7] тензорная производная можно найти только путем решения другой задачи на собственные значения.
Если выразить напряжение в терминах различий между компонентами,
σ 11 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 ; σ 22 − σ 33 = λ 2 ∂ W ∂ λ 2 − λ 3 ∂ W ∂ λ 3 {displaystyle sigma _ {11} -sigma _ {33} = lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} - lambda _ {3} ~ {cfrac {partial W} {partial lambda _ {3}}} ~; ~~ sigma _ {22} -sigma _ {33} = lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} - lambda _ {3} ~ {cfrac {частичный W} {частичный лямбда _ {3}}}} Если помимо несжимаемости имеем λ 1 = λ 2 {displaystyle lambda _ {1} = lambda _ {2}} σ 11 = σ 22 {displaystyle sigma _ {11} = sigma _ {22}}
σ 11 − σ 33 = σ 22 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 {displaystyle sigma _ {11} -sigma _ {33} = sigma _ {22} -sigma _ {33} = lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} - lambda _ {3} ~ {cfrac {частичный W} {частичный лямбда _ {3}}}}
Несжимаемые изотропные гиперупругие материалы Для несжимаемого изотропный сверхупругие материалы, функция плотности энергии деформации является W ( F ) = W ^ ( я 1 , я 2 ) {displaystyle W ({oldsymbol {F}}) = {hat {W}} (I_ {1}, I_ {2})}
σ = − п 1 + 2 [ ( ∂ W ^ ∂ я 1 + я 1 ∂ W ^ ∂ я 2 ) B − ∂ W ^ ∂ я 2 B ⋅ B ] = − п 1 + 2 [ ( ∂ W ∂ я ¯ 1 + я 1 ∂ W ∂ я ¯ 2 ) B ¯ − ∂ W ∂ я ¯ 2 B ¯ ⋅ B ¯ ] = − п 1 + λ 1 ∂ W ∂ λ 1 п 1 ⊗ п 1 + λ 2 ∂ W ∂ λ 2 п 2 ⊗ п 2 + λ 3 ∂ W ∂ λ 3 п 3 ⊗ п 3 {displaystyle {egin {align} {oldsymbol {sigma}} & = - p ~ {oldsymbol {mathit {1}}} + 2left [left ({cfrac {partial {hat {W}}} {partial I_ {1}}) } + I_ {1} ~ {cfrac {partial {hat {W}}} {partial I_ {2}}} ight) {oldsymbol {B}} - {cfrac {partial {hat {W}}} {partial I_ { 2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] & = - p ~ {oldsymbol {mathit {1}}} + 2left [left ({cfrac {partial W} {partial {ar {I}} _ {1}}} + I_ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ~ {ar {oldsymbol {B}}} - { cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {oldsymbol {B}}} cdot {ar {oldsymbol {B}}} ight] & = - p ~ {oldsymbol { mathit {1}}} + lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ mathbf {n} _ {1} otimes mathbf {n} _ {1} + lambda _ { 2} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ mathbf {n} _ {2} otimes mathbf {n} _ {2} + lambda _ {3} ~ {cfrac {partial W} { частичная лямбда _ {3}}} ~ mathbf {n} _ {3} otimes mathbf {n} _ {3} конец {выровнено}}} где п {displaystyle p}
σ 11 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 ; σ 22 − σ 33 = λ 2 ∂ W ∂ λ 2 − λ 3 ∂ W ∂ λ 3 {displaystyle sigma _ {11} -sigma _ {33} = lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} - lambda _ {3} ~ {cfrac {partial W} {partial lambda _ {3}}} ~; ~~ sigma _ {22} -sigma _ {33} = lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} - lambda _ {3} ~ {cfrac {частичный W} {частичный лямбда _ {3}}}} Если вдобавок я 1 = я 2 {displaystyle I_ {1} = I_ {2}}
σ = 2 ∂ W ∂ я 1 B − п 1 . {displaystyle {oldsymbol {sigma}} = 2 {cfrac {partial W} {partial I_ {1}}} ~ {oldsymbol {B}} - p ~ {oldsymbol {mathit {1}}} ~.} Если λ 1 = λ 2 {displaystyle lambda _ {1} = lambda _ {2}}
σ 11 − σ 33 = σ 22 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 {displaystyle sigma _ {11} -sigma _ {33} = sigma _ {22} -sigma _ {33} = lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} - lambda _ {3} ~ {cfrac {частичный W} {частичный лямбда _ {3}}}} Консистенция с линейной эластичностью Согласованность с линейной упругостью часто используется для определения некоторых параметров моделей гиперупругих материалов. Эти условия согласованности можно найти, сравнив Закон Гука с линеаризованной гиперупругостью при малых деформациях.
Условия согласованности изотропных гиперупругих моделей Чтобы изотропные гиперупругие материалы соответствовали изотропным линейная эластичность , зависимость напряжение – деформация должна иметь следующий вид в бесконечно малая деформация предел:
σ = λ т р ( ε ) 1 + 2 μ ε {displaystyle {oldsymbol {sigma}} = lambda ~ mathrm {tr} ({oldsymbol {varepsilon}}) ~ {oldsymbol {mathit {1}}} + 2mu {oldsymbol {varepsilon}}} где λ , μ {displaystyle lambda, mu} Константы Ламе . Функция плотности энергии деформации, соответствующая приведенному выше соотношению, имеет вид[1]
W = 1 2 λ [ т р ( ε ) ] 2 + μ т р ( ε 2 ) {displaystyle W = {frac {1} {2}} лямбда ~ [mathrm {tr} ({oldsymbol {varepsilon}})] ^ {2} + mu ~ mathrm {tr} ({oldsymbol {varepsilon}} ^ {2 })} Для несжимаемого материала т р ( ε ) = 0 {displaystyle mathrm {tr} ({oldsymbol {varepsilon}}) = 0}
W = μ т р ( ε 2 ) {displaystyle W = mu ~ mathrm {tr} ({oldsymbol {varepsilon}} ^ {2})} Для любой функции плотности энергии деформации W ( λ 1 , λ 2 , λ 3 ) {displaystyle W (лямбда _ {1}, лямбда _ {2}, лямбда _ {3})} [1]
W ( 1 , 1 , 1 ) = 0 ; ∂ W ∂ λ я ( 1 , 1 , 1 ) = 0 ∂ 2 W ∂ λ я ∂ λ j ( 1 , 1 , 1 ) = λ + 2 μ δ я j {displaystyle {egin {align} & W (1,1,1) = 0 ~; ~~ {cfrac {partial W} {partial lambda _ {i}}} (1,1,1) = 0 & {cfrac { частичное ^ {2} W} {частичное лямбда _ {i} частичное лямбда _ {j}}} (1,1,1) = лямбда + 2mu дельта _ {ij} конец {выровнено}}} Если материал несжимаемый, тогда вышеуказанные условия могут быть выражены в следующей форме.
W ( 1 , 1 , 1 ) = 0 ∂ W ∂ λ я ( 1 , 1 , 1 ) = ∂ W ∂ λ j ( 1 , 1 , 1 ) ; ∂ 2 W ∂ λ я 2 ( 1 , 1 , 1 ) = ∂ 2 W ∂ λ j 2 ( 1 , 1 , 1 ) ∂ 2 W ∂ λ я ∂ λ j ( 1 , 1 , 1 ) = я п d е п е п d е п т о ж я , j ≠ я ∂ 2 W ∂ λ я 2 ( 1 , 1 , 1 ) − ∂ 2 W ∂ λ я ∂ λ j ( 1 , 1 , 1 ) + ∂ W ∂ λ я ( 1 , 1 , 1 ) = 2 μ ( я ≠ j ) {displaystyle {egin {выравнивание} & W (1,1,1) = 0 & {cfrac {partial W} {partial lambda _ {i}}} (1,1,1) = {cfrac {partial W} {partial лямбда _ {j}}} (1,1,1) ~; ~~ {cfrac {partial ^ {2} W} {partial lambda _ {i} ^ {2}}} (1,1,1) = { cfrac {partial ^ {2} W} {partial lambda _ {j} ^ {2}}} (1,1,1) & {cfrac {partial ^ {2} W} {partial lambda _ {i} partial lambda _ {j}}} (1,1,1) = mathrm {independentof} ~ i, jeq i & {cfrac {partial ^ {2} W} {partial lambda _ {i} ^ {2}}} (1 , 1,1) - {cfrac {partial ^ {2} W} {partial lambda _ {i} partial lambda _ {j}}} (1,1,1) + {cfrac {partial W} {partial lambda _ { i}}} (1,1,1) = 2mu ~~ (ieq j) конец {выровнено}}} Эти условия могут быть использованы для нахождения соотношений между параметрами данной модели гиперупругости и модулями сдвига и объемного сжатия.
Условия согласованности несжимаемой я 1 {displaystyle I_ {1}} Многие эластомеры адекватно моделируются функцией плотности энергии деформации, которая зависит только от я 1 {displaystyle I_ {1}} W = W ( я 1 ) {displaystyle W = W (I_ {1})} я 1 = 3 , λ я = λ j = 1 {displaystyle I_ {1} = 3, lambda _ {i} = lambda _ {j} = 1}
W ( я 1 ) | я 1 = 3 = 0 и ∂ W ∂ я 1 | я 1 = 3 = μ 2 . {displaystyle W (I_ {1}) {iggr |} _ {I_ {1} = 3} = 0quad {ext {and}} quad {cfrac {partial W} {partial I_ {1}}} {iggr |} _ {I_ {1} = 3} = {frac {mu} {2}} ,.} Второе условие согласованности выше можно вывести, отметив, что
∂ W ∂ λ я = ∂ W ∂ я 1 ∂ я 1 ∂ λ я = 2 λ я ∂ W ∂ я 1 и ∂ 2 W ∂ λ я ∂ λ j = 2 δ я j ∂ W ∂ я 1 + 4 λ я λ j ∂ 2 W ∂ я 1 2 . {displaystyle {cfrac {partial W} {partial lambda _ {i}}} = {cfrac {partial W} {partial I_ {1}}} {cfrac {partial I_ {1}} {partial lambda _ {i}}} = 2lambda _ {i} {cfrac {partial W} {partial I_ {1}}} quad {ext {and}} quad {cfrac {partial ^ {2} W} {partial lambda _ {i} partial lambda _ {j }}} = 2delta _ {ij} {cfrac {partial W} {partial I_ {1}}} + 4lambda _ {i} lambda _ {j} {cfrac {partial ^ {2} W} {partial I_ {1} ^ {2}}} ,.} Эти соотношения затем можно подставить в условие согласованности для изотропных несжимаемых гиперупругих материалов.
использованная литература ^ а б c d Р. В. Огден, 1984 г., Нелинейные упругие деформации , ISBN 0-486-69648-0, Дувр. ^ Мур, А. Х. (2005). «Моделирование напряженно-деформированного поведения резины». Химия и технология резины . 78 (3): 391–425. Дои :10.5254/1.3547890 . ^ Гао, Н; Максимум; Ци, Н; Берри, С; Гриффит, BE; Ло, X. «Нелинейная модель митрального клапана человека с конечной деформацией и взаимодействием жидкости и структуры» . Int J Numer Method Biomed Eng . 30 : 1597–613. Дои :10.1002 / cnm.2691 . ЧВК 4278556 PMID 25319496 . ^ Jia, F; Бен Амар, М. Billoud, B; Шарье, Б. «Морфоэластичность в развитии бурых водорослей. Ectocarpus siliculosus : от округления ячейки к ветвлению " . Интерфейс J R Soc . 14 : 20160596. Дои :10.1098 / rsif.2016.0596 . ЧВК 5332559 PMID 28228537 . ^ Ю. Басар, 2000, Нелинейная сплошная механика твердого тела, Springer, с. 157. ^ Фокс и Капур, Скорость изменения собственных значений и собственных векторов , Журнал AIAA , 6 (12) 2426–2429 (1968) ^ Friswell MI. Производные повторяющихся собственных значений и связанных с ними собственных векторов. Журнал вибрации и акустики (ASME) 1996; 118: 390–397. Смотрите также 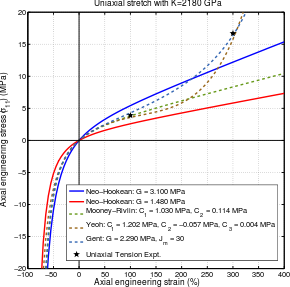







![{mathbf E} = {frac {1} {2}} left [(abla _ {{{mathbf X}}} {mathbf u}) ^ {T} + abla _ {{{mathbf X}}} {mathbf u } + (abla _ {{{mathbf X}}} {mathbf u}) ^ {T} cdot abla _ {{{mathbf X}}} {mathbf u} ight] ,!](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb57038f53e8acd75c977dd33dc650dd27913b2c)



![W ({oldsymbol {E}}) = {frac {lambda} {2}} [{ext {tr}} ({oldsymbol {E}})] ^ {2} + mu {ext {tr}} ({oldsymbol {E}} ^ {2})](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9c069514727f98b79fe8f70daaacd4e1750cbc)























![{egin {выровнено} {oldsymbol {sigma}} & = {cfrac {2} {{sqrt {I_ {3}}}}} left [left ({cfrac {partial {hat {W}}} {partial I_ {1 }}} + I_ {1} ~ {cfrac {partial {hat {W}}} {partial I_ {2}}} ight) {oldsymbol {B}} - {cfrac {partial {hat {W}}} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] +2 {sqrt {I_ {3}}} ~ {cfrac {partial {hat {W}}} {partial I_ {3 }}} ~ {oldsymbol {{mathit {1}}}} & = {cfrac {2} {J}} left [{cfrac {1} {J ^ {{2/3}}}} left ({cfrac {partial {ar {W}}} {partial {ar {I}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I}} _ {2}}} ight) {oldsymbol {B}} - {cfrac {1} {J ^ {{4/3}}}} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] & qquad qquad + left [{cfrac {partial {ar {W}}} {partial J}} - {cfrac {2} {3J}} слева ({ar {I}} _ {1} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ight) ight] ~ {oldsymbol {{mathit {1}) }}} & = {cfrac {2} {J}} left [left ({cfrac {partial {ar {W}}} {partial {ar {I}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I} }} _ {2}}} ight) {ar {{oldsymbol {B}}}} - {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ~ {ar {{oldsymbol {B}}}} cdot {ar {{oldsymbol {B}}}} ight] + left [{cfrac {partial {ar {W}}} {partial J}} - {cfrac {2} {3J }} слева ({ar {I}} _ {1} ~ {cfrac {partial {ar {W}}}} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial {ar {W}}} {partial {ar {I}} _ {2}}} ight) ight] ~ {oldsymbol {{mathit {1}}}} & = {cfrac {lambda _ {1}} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac {partial {ilde {W}}} {partial lambda _ {1}}} ~ {mathbf { n}} _ {1} otimes {mathbf {n}} _ {1} + {cfrac {lambda _ {2}} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac { частичное {ilde {W}}} {частичное лямбда _ {2}}} ~ {mathbf {n}} _ {2} otimes {mathbf {n}} _ {2} + {cfrac {lambda _ {3}} { lambda _ {1} lambda _ {2} lambda _ {3}}} ~ {cfrac {partial {ilde {W}}} {partial lambda _ {3}}} ~ {mathbf {n}} _ {3} otimes {mathbf {n}} _ {3} конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c827a98c19f82fbc33bc4787ff6e1aaa021d5d22)








![{oldsymbol {sigma}} = {cfrac {2} {J}} ~ left [{cfrac {partial W} {partial I_ {1}}} ~ {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T } + {cfrac {partial W} {partial I_ {2}}} ~ (I_ {1} ~ {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T} - {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T} cdot {oldsymbol {F}} cdot {oldsymbol {F}} ^ {T}) + {cfrac {partial W} {partial I_ {3}}} ~ I_ {3} ~ {oldsymbol {{mathit {1}}}} полет]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e14aca126ea518e5e3e0132e4fd899deadbc3ad)


![{oldsymbol {sigma}} = {cfrac {2} {{sqrt {I_ {3}}}}} ~ left [left ({cfrac {partial W} {partial I_ {1}}} + I_ {1} ~ { cfrac {частичный W} {частичный I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {частичный I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B} } ight] + 2 ~ {sqrt {I_ {3}}} ~ {cfrac {partial W} {partial I_ {3}}} ~ {oldsymbol {{mathit {1}}}} ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1ee0c6cf0b91150820746d66e9a5e38e7cfe65)



![{oldsymbol {sigma}} = 2left [left ({cfrac {partial W} {partial I_ {1}}} + I_ {1} ~ {cfrac {partial W} {partial I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] -p ~ {oldsymbol {{mathit {1}}}} ~ .](https://wikimedia.org/api/rest_v1/media/math/render/svg/6381092927f1ab91630b3e401879855dbfa465d0)












![{oldsymbol {sigma}} = {cfrac {2} {J}} ~ left [left ({cfrac {partial W} {partial I_ {1}}}} + J ^ {{2/3}}} ~ {ar {I }} _ {1} ~ {cfrac {partial W} {partial I_ {2}}} ight) ~ {oldsymbol {B}} - {cfrac {partial W} {partial I_ {2}}} ~ {oldsymbol {B }} cdot {oldsymbol {B}} ight] + 2 ~ J ~ {cfrac {partial W} {partial I_ {3}}} ~ {oldsymbol {{mathit {1}}}} ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4f30443899568890a1c8f543ec6a9524c996172)

![{egin {выровнено} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [left (J ^ {{- 2/3}}} ~ {cfrac {partial W} {partial {ar {I) }} _ {1}}} + J ^ {{- 2/3}} ~ {ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}} } ight) ~ {oldsymbol {B}} - J ^ {{- 4/3}} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] + & qquad 2 ~ J ~ left [- {cfrac {1} {3}} ~ J ^ {{- 2}} ~ left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ { 2}}} ight) + {cfrac {1} {2}} ~ J ^ {{- 1}} ~ {cfrac {partial W} {partial J}} ight] ~ {oldsymbol {{mathit {1}}} } конец {выровнен}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/942d309f640a99c84f20f0f4d241b013e1a933d6)
![{egin {выравнивается} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [{cfrac {1} {J ^ {{2/3}}}} ~ left ({cfrac {partial W } {partial {ar {I}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial W} {частичный {ar {I}} _ {2}}} полёт) ~ {oldsymbol {B}} - {cfrac {1} {J ^ {{4/3}}}} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {oldsymbol {B }} cdot {oldsymbol {B}} ight] & qquad + left [{cfrac {partial W} {partial J}} - {cfrac {2} {3J}} left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ { 2}}} ight) ight] {oldsymbol {{mathit {1}}}} конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8d623e7b2f5d1d9f08bd3c2b5a5b7d833f8df)

![{egin {выровнено} {oldsymbol {sigma}} & = {cfrac {2} {J}} ~ left [left ({cfrac {partial W} {partial {ar {I}}} _ {1}}} + {ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ~ {ar {{oldsymbol {B}}}} - {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {{oldsymbol {B}}}} cdot {ar {{oldsymbol {B}}}} ight] & qquad + left [{cfrac {partial W } {partial J}} - {cfrac {2} {3J}} left ({ar {I}} _ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {1}}} + 2 ~ {ar {I}} _ {2} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ight] {oldsymbol {{mathit {1}}}} end { выровнен}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8e447cd3da810efbd1307341195ecdcade76c7a)


![{oldsymbol {sigma}} = 2left [left ({cfrac {partial W} {partial {ar {I}}} _ {1}}} + I_ {1} ~ {cfrac {partial W} {partial {ar {I}}) } _ {2}}} ight) ~ {ar {{oldsymbol {B}}}} - {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {{oldsymbol {B }}}} cdot {ar {{oldsymbol {B}}}} ight] -p ~ {oldsymbol {{mathit {1}}}} ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0104ea1124e91b8d004bdb373b069edcc94d576f)





![{egin {align} {cfrac {partial W} {partial {oldsymbol {C}}}}} & = {cfrac {partial W} {partial lambda _ {1}}} ~ {cfrac {partial lambda _ {1}} { partial {oldsymbol {C}}}} + {cfrac {partial W} {частичное лямбда _ {2}}} ~ {cfrac {частичное лямбда _ {2}} {частичное {oldsymbol {C}}}} + {cfrac { partial W} {частичный лямбда _ {3}}} ~ {cfrac {частичный лямбда _ {3}} {partial {oldsymbol {C}}}} & = {oldsymbol {R}} ^ {T} cdot left [{ cfrac {1} {2lambda _ {1}}} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ {mathbf {n}} _ {1} otimes {mathbf {n}} _ {1} + {cfrac {1} {2lambda _ {2}}} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ {mathbf {n}} _ {2} otimes {mathbf {n}} _ { 2} + {cfrac {1} {2lambda _ {3}}} ~ {cfrac {partial W} {partial lambda _ {3}}} ~ {mathbf {n}} _ {3} otimes {mathbf {n}} _ {3} ight] cdot {oldsymbol {R}} конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7525fe32c1f006a7800f672d51035a43e2802c90)

![{oldsymbol {sigma}} = {cfrac {2} {J}} ~ {oldsymbol {V}} cdot left [{cfrac {1} {2lambda _ {1}}} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ {mathbf {n}} _ {1} otimes {mathbf {n}} _ {1} + {cfrac {1} {2lambda _ {2}}} ~ {cfrac {частичный W} {частичный lambda _ {2}}} ~ {mathbf {n}} _ {2} otimes {mathbf {n}} _ {2} + {cfrac {1} {2lambda _ {3}}} ~ {cfrac {частичное W} {частичная лямбда _ {3}}} ~ {mathbf {n}} _ {3} otimes {mathbf {n}} _ {3} ight] cdot {oldsymbol {V}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/977230f6bcdfd24e95c31388332eadf83658fca3)



![{oldsymbol {sigma}} = {cfrac {1} {lambda _ {1} lambda _ {2} lambda _ {3}}} ~ left [lambda _ {1} ~ {cfrac {partial W} {partial lambda _ { 1}}} ~ {mathbf {n}} _ {1} otimes {mathbf {n}} _ {1} + lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ { mathbf {n}} _ {2} otimes {mathbf {n}} _ {2} + lambda _ {3} ~ {cfrac {partial W} {partial lambda _ {3}}} ~ {mathbf {n}} _ {3} otimes {mathbf {n}} _ {3} ight]](https://wikimedia.org/api/rest_v1/media/math/render/svg/98f1a3e0369450e0ee8ec83c6917e96874302e62)








![{egin {выровнено} {oldsymbol {sigma}} & = - p ~ {oldsymbol {{mathit {1}}}} + 2left [left ({cfrac {partial {hat {W}}} {partial I_ {1}}) } + I_ {1} ~ {cfrac {partial {hat {W}}} {partial I_ {2}}} ight) {oldsymbol {B}} - {cfrac {partial {hat {W}}} {partial I_ { 2}}} ~ {oldsymbol {B}} cdot {oldsymbol {B}} ight] & = - p ~ {oldsymbol {{mathit {1}}}} + 2left [left ({cfrac {partial W} {partial {ar {I}} _ {1}}} + I_ {1} ~ {cfrac {partial W} {partial {ar {I}} _ {2}}} ight) ~ {ar {{oldsymbol {B}} }} - {cfrac {partial W} {partial {ar {I}} _ {2}}} ~ {ar {{oldsymbol {B}}}} cdot {ar {{oldsymbol {B}}}} ight] & = - p ~ {oldsymbol {{mathit {1}}}} + lambda _ {1} ~ {cfrac {partial W} {partial lambda _ {1}}} ~ {mathbf {n}} _ {1} otimes {mathbf {n}} _ {1} + lambda _ {2} ~ {cfrac {partial W} {partial lambda _ {2}}} ~ {mathbf {n}} _ {2} otimes {mathbf {n}} _ {2} + lambda _ {3} ~ {cfrac {partial W} {partial lambda _ {3}}} ~ {mathbf {n}} _ {3} otimes {mathbf {n}} _ {3} end { выровнен}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a01e1483b139b0476ce6e30d37db183a0f1fa600)


![W = {frac {1} {2}} лямбда ~ [{mathrm {tr}} ({oldsymbol {varepsilon}})] ^ {2} + mu ~ {mathrm {tr}} ({oldsymbol {varepsilon}} ^ {2})](https://wikimedia.org/api/rest_v1/media/math/render/svg/be5e49f19ce38854b20045fed38b47140cbc09f1)







