Узел (математика) - Knot (mathematics)

Эта статья о математическом объекте. Для использования в других целях см. Узел (значения).
Таблица всех простые узлы с семью переходы или меньше (не включая зеркальные изображения).
Узел сверху становится трилистник соединив концы.
Треугольник связан с узлом-трилистником.
74 крендель ссылка узел

В математика, а узел является встраивание из топологический круг S1 в 3-х мерном Евклидово пространство, р3 (также известен как E3), считая с точностью до непрерывных деформаций (изотопии ).

Решающее различие между стандартными математическими и общепринятыми понятиями узел заключается в том, что математические узлы замкнуты - нет конца, который можно было бы завязать или развязать математическим узлом. Физические свойства, такие как трение и толщина, также не применяются, хотя существуют математические определения узла, которые учитывают такие свойства. Период, термин узел также применяется к вложениям S j в Sп, особенно в случае j = п − 2. Раздел математики, изучающий узлы, известен как теория узлов, и имеет много простых отношений с теория графов.

Формальное определение

Узел - это встраивание из круг (S1) в трехмерный Евклидово пространство (р3).[1] или 3-сфера, S3, так как 3-сфера компактный.[2] [Примечание 1] Два узла считаются эквивалентными, если существует окружающая изотопия между ними.[3]

Проекция

Узел в р3 (или, альтернативно, в 3-сфера, S3), можно спроецировать на плоскостьр2 (соответственно сфера  S2). Эта проекция почти всегда регулярный, что означает, что это инъективный везде, кроме конечное число точек пересечения, которые являются проекциями только два очка узла, и эти точки не коллинеарен. В этом случае, выбрав сторону проекции, можно полностью закодировать изотопия класс узла по его регулярной проекции путем записи простой информации о пере / занижении на этих пересечениях. С точки зрения теории графов, регулярная проекция узла, или диаграмма узла таким образом, четырехвалентный планарный граф с пере / недодекорированными вершинами. Локальные модификации этого графа, которые позволяют переходить от одной диаграммы к любой другой диаграмме того же узла (вплоть до окружающего изотопия самолета) называются Рейдемейстер движется.

  • Рейдемейстер, ход 1

  • Рейдемейстер, ход 2

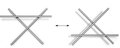
  • Рейдемейстер, ход 3

Виды узлов

Узел можно развязать, если разорвать петлю.

Самый простой узел, называемый развязанный или тривиальный узел, это круглая окружность, вложенная в р3.[4] В обычном смысле этого слова развязка вовсе не «завязана узлом». Простейшие нетривиальные узлы - это трилистник (31 в таблице), узел восьмерка (41) и узел с лапчаткой (51).[5]

Несколько узлов, связанных или запутанных вместе, называются ссылки. Узлы - это звенья с одним компонентом.

Приручение против диких узлов

Дикий узел.

А многоугольный узел - это узел, образ в р3 это союз из конечный набор из отрезки линии.[6] А приручить узел - это любой узел, эквивалентный многоугольному узлу.[6][Заметка 2] Неприрученные сучки называются дикий,[7] и может иметь патологический поведение.[7] В теории узлов и 3-х коллекторный теория, часто прилагательное «приручить» опускается. Гладкие сучки, например, всегда ручные.

Узел в рамке

А узел в рамке является продолжением ручного узла до вложения полнотория D2 × S1 в S3.

В обрамление узла это номер ссылки изображения ленты я × S1 с узлом. Узел в обрамлении можно рассматривать как встроенную ленту, а обрамление - это (подписанное) количество витков.[8] Это определение обобщается на аналогичное для ссылки в рамке. Ссылки в рамке называются эквивалент если их продолжения на полнотории объемлющие изотопны.

Ссылка в рамке диаграммы представляют собой схемы связей, на которых каждый компонент отмечен для обозначения кадрирования целое число представляющий наклон относительно меридиана и предпочтительной долготы. Стандартный способ просмотра схемы ссылок без маркировки, представляющей ссылку в рамке, - использовать обрамление доски. Это обрамление получается путем преобразования каждого компонента в плоскую ленту, лежащую на плоскости. Тип I Ход Рейдемейстера явно изменяет обрамление доски (меняет количество витков ленты), но два других хода - нет. Замена типа, который я перемещаю, на измененный тип, который я перемещаю, дает результат для диаграмм связей с обрамлением доски, аналогичный теореме Рейдемейстера: диаграммы связей с обрамлением доски представляют эквивалентные обрамленные ссылки тогда и только тогда, когда они связаны последовательностью ) ходов I, II и III типов, на узле можно определить бесконечно много оснащений. Предположим, что нам дан узел с фиксированным оснащением. Можно получить новое обрамление из существующего, разрезав ленту и закрутив ее вокруг узла на целое число, кратное 2π, а затем снова приклеив его на место, где мы разрезали. Таким образом, получается новое оснащение из старого, с точностью до отношения эквивалентности для оснащенных узлов, оставляя узел неподвижным. [9] Кадрирование в этом смысле связано с числом поворотов, которые векторное поле совершает вокруг узла. Зная, сколько раз векторное поле закручено вокруг узла, можно определить векторное поле с точностью до диффеоморфизма, а класс эквивалентности кадрирования полностью определяется этим целым числом, называемым кадрирующим целым.

Узел дополнение

Узел, дополнение которого имеет нетривиальное JSJ-разложение.

Учитывая узел в 3-сфере, узел дополнения - это все точки 3-сферы, не содержащиеся в узле. Основным Теорема Гордона и Люке утверждает, что не более двух узлов имеют гомеоморфные дополнения (исходный узел и его зеркальное отражение). По сути, это превращает изучение узлов в изучение их дополнений и, в свою очередь, в Теория 3-многообразий.[10]

Разложение JSJ

Основная статья: Разложение JSJ

В Разложение JSJ и Теорема терстона о гиперболизации сводит изучение узлов в 3-сфере к изучению различных геометрических многообразий с помощью сращивание или спутниковые операции. В изображенном узле JSJ-разложение разбивает дополнение на объединение трех многообразий: двух трилистник дополняет и дополнение Кольца Борромео. Дополнение трилистника имеет геометрию ЧАС2 × р, а дополнение к кольцам Борромео имеет геометрию ЧАС3.

Гармонические узлы

Параметрические представления узлов называются гармоническими узлами. Аарон Траутвейн в своей кандидатской диссертации составил параметрические представления для всех узлов, включая узлы с числом пересечения 8.[11]

Приложения к теории графов

Таблица всех простые узлы до семи переходы представлен как схемы узлов с их медиальный график.

Медиальный график

Основная статья: Медиальный график
KnotCheckerboard.svg
Планарный граф со знаком, связанный с узловой диаграммой.
Левая направляющая
Правый гид

Еще одно удобное представление диаграмм узлов [12][13] был представлен Питер Тейт в 1877 г.[14][15]

Любая узловая диаграмма определяет плоский график чьи вершины являются перекрестками, а ребра - путями между последовательными перекрестками. Ровно одна грань этого плоского графа неограничена; каждый из остальных гомеоморфный к двумерному диск. Раскрасьте эти грани в черный или белый цвет, чтобы неограниченная грань была черной, а любые две грани, которые имеют общий граничный край, имели противоположные цвета. В Теорема Жордана означает, что существует ровно одна такая раскраска.

Мы строим новый плоский граф, вершинами которого являются белые грани, а ребра соответствуют перекресткам. Мы можем пометить каждое ребро в этом графе как левое или правое ребро, в зависимости от того, какой поток кажется пересекающим другой, когда мы рассматриваем соответствующее пересечение с одной из конечных точек ребра. Левый и правый края обычно обозначаются обозначением левого края + и правого края - или рисованием левых краев сплошными линиями и правых краев пунктирными линиями.

Исходная диаграмма узлов - это медиальный график этого нового плоского графа, причем тип каждого пересечения определяется знаком соответствующего ребра. Изменение знака каждый край соответствует отражающему узел в зеркале.

Вложение без звеньев и узлов

Основная статья: вложение без ссылок
Семь графиков в Семья Петерсен. Независимо от того, как эти графы вложены в трехмерное пространство, некоторые два цикла будут иметь ненулевые номер ссылки.

В двух измерениях только планарные графы могут быть вложены в евклидову плоскость без пересечений, но в трех измерениях, любые неориентированный граф можно встраивать в пространство без переходов. Однако пространственным аналогом планарных графов являются графы с вложения без ссылок и безузловые вложения. Вложение без связей - это вложение графа, обладающее тем свойством, что любые два цикла являются несвязанный; безузловое вложение - это вложение графа, обладающее тем свойством, что любой цикл является несвязанный. Графы с вложениями без ссылок имеют характеристика запрещенного графа с участием Семья Петерсен, набор из семи графов, которые внутренне связаны: независимо от того, как они встроены, некоторые два цикла будут связаны друг с другом.[16] Полная характеристика графов с безузловыми вложениями неизвестна, но полный график K7 является одним из минимальных запрещенных графов для безузлового вложения: как бы K7 встроен, он будет содержать цикл, образующий трилистник.[17]

Обобщение

В современной математике термин узел иногда используется для описания более общего явления, связанного с вложениями. Учитывая многообразие M с подмногообразием N, иногда говорят N может быть завязан M если существует вложение N в M который не изотопен N. Традиционные узлы образуют случай, когда N = S1 и M = р3 или M = S3.[18][19]

В Теорема Шенфлиса утверждает, что круг не узел в 2-сфере: каждая топологическая окружность в 2-сфере изотопна геометрической окружности.[20] Теорема александра утверждает, что 2-сфера не создает гладких (или PL или ручных топологически) узлов в 3-сфере.[21] В категории ручной топологии известно, что п-сфера не завязывается в п + 1-сфера для всех п. Это теорема Мортон Браун, Барри Мазур, и Марстон Морс.[22] В Александр рогатый шар это пример завязанной 2-сферы в 3-сфере, которая не является ручной.[23] В гладкой категории п-сфера, как известно, не завязывается п + 1-сфера предоставляется п ≠ 3. Дело п = 3 - давно нерешенная проблема, тесно связанная с вопросом: допускает ли 4-шар экзотическая гладкая структура ?

Андре Хефлигер доказал, что нет гладких j-размерные узлы в Sп предоставлена 2п − 3j − 3 > 0, и привел дополнительные примеры узловых сфер для всех п > j ≥ 1 такой, что 2п − 3j − 3 = 0. п − j называется коразмерность узла. Интересным аспектом работы Хефлигера является то, что изотопические классы вложений S j в Sп образуют группу с групповой операцией, задаваемой суммой соединения, при условии, что совпадение больше двух. Хефлигер основывал свою работу на Стивен Смейл с час-теорема -кобордизм. Одна из теорем Смейла состоит в том, что когда мы имеем дело с узлами в когерентности больше двух, даже неэквивалентные узлы имеют диффеоморфные дополнения. Это придает предмету особый колорит, нежели теория узлов с размерностью 2. Если допустить топологические или PL-изотопии, Кристофер Зееман доказал, что сферы не связываются, когда размерность больше 2. См. обобщение на многообразия.

Смотрите также

Заметки

  1. ^ Обратите внимание, что 3-сфера эквивалентна р3 с единственной точкой, добавленной на бесконечности (см. одноточечная компактификация ).
  2. ^ Узел ручной тогда и только тогда, когда его можно представить в виде конечного замкнутая многоугольная цепь

использованная литература

  1. ^ Армстронг (1983), п. 213.
  2. ^ Кромвель (2004), п. 33; Адамс (1994) С. 246–250.
  3. ^ Кромвель (2004), п. 5.
  4. ^ Адамс (1994), п. 2.
  5. ^ Адамс (1994), Таблица 1.1, стр. 280; Ливингстон (1996), Приложение A: Таблица узлов, стр. 221.
  6. ^ а б Армстронг (1983), п. 215.
  7. ^ а б Чарльз Ливингстон (1993). Теория узлов. Издательство Кембриджского университета. п. 11. ISBN  978-0-88385-027-5.
  8. ^ Кауфман, Луи Х. (1990). «Инвариант регулярной изотопии» (PDF). Труды Американского математического общества. 318 (2): 417–471. Дои:10.1090 / S0002-9947-1990-0958895-7.
  9. ^ Эльхамдади, Мохамед; Хаджид, Мустафа; Иштван, Кайл (2019), Обрамленные узлы, препринт arXiv arXiv: 1910.10257, arXiv:1910.10257.
  10. ^ Адамс (1994) С. 261–262.
  11. ^ Аарон Траутвайн, доктор философии. Диссертация: Гармонические узлы, Университет Айовы, май 1994 г.
  12. ^ Адамс, Колин С. (2001). Книга узлов. Американское математическое общество. С. 52–55.
  13. ^ Entrelacs.net учебник
  14. ^ Тейт, Питер Г. (1876–1877). "На узлах I". Труды Королевского общества Эдинбурга. 28: 145–190. Дои:10.1017 / S0080456800090633. Пересмотрено 11 мая 1877 г.
  15. ^ Тейт, Питер Г. (1876–1877). «По ссылкам (аннотация)». Труды Королевского общества Эдинбурга. 9 (98): 321–332. Дои:10.1017 / S0370164600032363.
  16. ^ Робертсон, Нил; Сеймур, Пол; Томас, Робин (1993), "Обзор беззвеньевых вложений", в Робертсон, Нил; Сеймур, Пол (ред.), Теория графической структуры: Учеб. Совместная летняя научная конференция AMS – IMS – SIAM по минорам графов (PDF), Современная математика, 147, Американское математическое общество, стр. 125–136..
  17. ^ Рамирес Альфонсин, Дж. Л. (1999), "Пространственные графы и ориентированные матроиды: трилистник", Дискретная и вычислительная геометрия, 22 (1): 149–158, Дои:10.1007 / PL00009446.
  18. ^ Картер, Дж. Скотт; Сайто, Масахико (1998). Узловые поверхности и их диаграммы. Математические обзоры и монографии. 55. Провиденс, Род-Айленд: Американское математическое общество. ISBN  0-8218-0593-2. Г-Н  1487374.
  19. ^ Камада, Сейичи (2017). Поверхностные узлы в 4-м пространстве. Монографии Спрингера по математике. Сингапур: Спрингер. Дои:10.1007/978-981-10-4091-7. ISBN  978-981-10-4090-0. Г-Н  3588325.
  20. ^ Хокинг, Джон Дж .; Янг, Гейл С. (1988). Топология (2-е изд.). Нью-Йорк: Dover Publications. п. 175. ISBN  0-486-65676-4. Г-Н  1016814.
  21. ^ Калегари, Дэнни (2007). Слоения и геометрия трехмерных многообразий. Оксфордские математические монографии. Издательство Оксфордского университета. п. 161. ISBN  978-0-19-857008-0. Г-Н  2327361.
  22. ^ Мазур, Барри (1959). «О вложениях сфер». Бюллетень Американского математического общества. 65 (2): 59–65. Дои:10.1090 / S0002-9904-1959-10274-3. Г-Н  0117693. Браун, Мортон (1960). «Доказательство обобщенной теоремы Шенфлиса». Бюллетень Американского математического общества. 66 (2): 74–76. Дои:10.1090 / S0002-9904-1960-10400-4. Г-Н  0117695. Морс, Марстон (1960). «Уменьшение проблемы расширения Шенфлиса». Бюллетень Американского математического общества. 66 (2): 113–115. Дои:10.1090 / S0002-9904-1960-10420-X. Г-Н  0117694.
  23. ^ Александр, Дж. У. (1924). «Пример просто соединенной поверхности, ограничивающей не просто соединенную область». Труды Национальной академии наук Соединенных Штатов Америки. Национальная академия наук. 10 (1): 8–10. Bibcode:1924ПНАС ... 10 .... 8А. Дои:10.1073 / pnas.10.1.8. ISSN  0027-8424. JSTOR  84202. ЧВК  1085500. PMID  16576780.
  • Адамс, Колин С. (1994). Книга узлов: элементарное введение в математическую теорию узлов. В. Х. Фриман и компания.CS1 maint: ref = harv (ссылка на сайт)
  • Армстронг, М. А. (1983) [1979]. Базовая топология. Тексты для бакалавриата по математике. Нью-Йорк: Springer-Verlag. ISBN  0-387-90839-0.CS1 maint: ref = harv (ссылка на сайт)
  • Кромвель, Питер Р. (2004). Узлы и ссылки. Издательство Кембриджского университета, Кембридж. Дои:10.1017 / CBO9780511809767. ISBN  0-521-83947-5. Г-Н  2107964.CS1 maint: ref = harv (ссылка на сайт)
  • Фармер, Дэвид В .; Стэнфорд, Теодор Б. (1995). Узлы и поверхности: руководство к открытию математики.CS1 maint: ref = harv (ссылка на сайт)
  • Ливингстон, Чарльз (1996). Теория узлов. Математическая ассоциация Америки.CS1 maint: ref = harv (ссылка на сайт)

внешние ссылки