Юрген Элерс - Jürgen Ehlers

Юрген Элерс
Юрген Элерс.jpg
На церемонии награждения медалью Карлова университета в Потсдаме, сентябрь 2007 г.
Родившийся(1929-12-29)29 декабря 1929 г.
Гамбург, Германия
Умер20 мая 2008 г.(2008-05-20) (78 лет)
Потсдам, Бранденбург, Германия
НациональностьНемецкий
Альма-матерГамбургский университет
ИзвестенОбщая теория относительности
Математическая физика
НаградыМедаль Макса Планка (2002)
Научная карьера
ПоляФизика
УчрежденияГамбургский университет
Институт астрофизики Макса Планка
Институт Макса Планка гравитационной физики
ДокторантПаскуаль Джордан
Часть серии по
Физическая космология
Изображение полного неба, полученное по данным WMAP за девять лет
  • Ааронсон
  • Альфвен
  • Альфер
  • Бхарадвадж
  • Коперник
  • де Ситтер
  • Дике
  • Эддингтон
  • Элерс
  • Эйнштейн
  • Эллис
  • Фридман
  • Галилео
  • Гамов
  • Гут
  • Хаббл
  • Лемэтр
  • Linde
  • Mather
  • Ньютон
  • Penzias
  • Вбивать в голову
  • Шмидт
  • Шварцшильд
  • Гладкий
  • Старобинский
  • Steinhardt
  • Suntzeff
  • Сюняев
  • Толман
  • Уилсон
  • Зельдович
    • Категория Категория
    • Крабовидная туманность.jpg Астрономический портал

    Юрген Элерс (Немецкий: [ˈJʏʁɡŋ̩ ˈeːlɐs]; 29 декабря 1929 - 20 мая 2008) был немец физик кто способствовал пониманию Альберт Эйнштейн теория общая теория относительности. От аспирантуры и аспирантуры в Паскуаль Джордан группа исследователей относительности в Гамбургский университет, он занимал различные должности в качестве лектора, а затем профессора, прежде чем присоединиться к Институт астрофизики Макса Планка в Мюнхен как режиссер. В 1995 году он стал директором-учредителем вновь созданной Институт Макса Планка гравитационной физики в Потсдам, Германия.

    Исследования Элерса были сосредоточены на основах общей теории относительности, а также на ее приложениях к астрофизика. Он сформулировал подходящую классификацию точные решения к Полевые уравнения Эйнштейна и доказал Теорема Элерса – Герена – Сакса. что оправдывает применение простых, общерелятивистских моделей вселенных к современным космология. Он создал пространство-время ориентированное описание гравитационное линзирование и прояснил отношения между моделями, сформулированными в рамках общей теории относительности, и моделями Ньютоновская гравитация. Кроме того, Элерс проявлял большой интерес как к истории, так и к философия физики и был ярым популяризатором науки.

    биография

    Ранние годы

    Юрген Элерс родился в Гамбурге. Он учился в государственных школах с 1936 по 1949 год, а затем изучал физику, математику и философию в Гамбургский университет с 1949 по 1955 г. В зимнем семестре 1955–56 гг. сдал экзамен учителя средней школы (Staatsexamen ), но вместо того, чтобы стать учителем, провел аспирантуру с Паскуаль Джордан, который выступал в качестве его научного руководителя. Докторская работа Элерса была посвящена построению и характеристике решения из Уравнения поля Эйнштейна. Он получил докторскую степень по физике в Гамбургском университете в 1958 году.[1]

    До приезда Элерса основное исследование группы Джордана было посвящено скаляр-тензор модификация общей теории относительности, которая позже стала известна как Теория Джордана – Бранса – Дике.. Эта теория отличается от общей теории относительности тем, что гравитационная постоянная заменяется переменной поле. Элерс сыграл важную роль в изменении фокуса группы на структуру и интерпретацию первоначальной теории Эйнштейна.[2] Среди других участников группы были Вольфганг Кундт, Райнер К. Сакс и Манфред Трюмпер.[3]У группы были тесные рабочие отношения с Отто Хекманн и его ученик Энгельберт Шюкинг в Гамбургер Стернварте, городская обсерватория. В числе гостей коллоквиума группы Вольфганг Паули, Джошуа Голдберг и Питер Бергманн.[4]

    В 1961 году, будучи помощником Джордана, Элерс получил свое абилитация, квалифицируя его на немецкую профессуру. Затем он занимал преподавательские и исследовательские должности в Германии и США, а именно в Кильский университет, Сиракузский университет и Гамбургский университет. С 1964 по 1965 год он был в Научно-исследовательский центр Юго-Запада в Даллас. С 1965 по 1971 год занимал различные должности в Альфред Шильд группа в Техасский университет в Остине, начиная с Доцент а в 1967 году получил должность профессора. За это время он работал приглашенным профессором в университетах Вюрцбург и Бонн.[5]

    Мюнхен

    В 1970 году Элерс получил предложение присоединиться к Институт физики и астрофизики Макса Планка в Мюнхен в качестве директора отдела теории гравитации.[6] Элерса предложил Людвиг Бирманн, директор института в то время. Когда Элерс присоединился к институту в 1971 году, он также стал адъюнкт-профессором Мюнхенской Университет Людвига-Максимилиана. В марте 1991 г. институт разделился на Институт физики Макса Планка и Институт астрофизики Макса Планка, где нашла приют отдел Элерса.[7] За 24 года его пребывания в должности в его исследовательской группе, в частности, работали: Гэри Гиббонс, Джон Стюарт и Бернд Шмидт, а также приглашенные ученые, включая Абхай Аштекар, Деметриос Христодулу и Брэндон Картер.[8]

    Один из Элерсов докторанты в Мюнхене был Райнхард Брейер, который позже стал главным редактором журнала Spektrum der Wissenschaft, немецкое издание научно-популярного журнала Scientific American.[9]

    Потсдам

    Когда немецкие научные учреждения реорганизовались после Воссоединение Германии В 1990 году Элерс лоббировал создание института Общества Макса Планка, занимающегося исследованиями теории гравитации. 9 июня 1994 г. Общество решило открыть Институт Макса Планка гравитационной физики в Потсдам. Институт начал свою работу 1 апреля 1995 года, когда Элерс был его директором-основателем и руководителем отдела основ и математики общей теории относительности.[10] Затем Элерс руководил созданием второго отдела института, посвященного гравитационная волна исследования и возглавил Бернард Ф. Шютц. 31 декабря 1998 года Элерс вышел на пенсию и стал директором-основателем. заслуженный.[11]

    Элерс продолжал работать в институте до своей смерти 20 мая 2008 года.[12] Он оставил после себя жену Аниту Элерс, четверых детей, Мартина, Катрин, Дэвида и Макса, а также пятерых внуков.[13]

    Исследование

    Исследования Элерса были в области общей теории относительности. В частности, он внес вклад в космология, теория гравитационные линзы и гравитационные волны. Его главной заботой было прояснить математическую структуру общей теории относительности и ее следствия, отделив строгие доказательства от эвристический домыслы.[14]

    Точные решения

    В своей докторской диссертации Элерс обратился к вопросу, который должен был сформировать его исследования на протяжении всей его жизни. Он искал точные решения Уравнения Эйнштейна: модели вселенных в соответствии с законами общей теории относительности, которые достаточно просты, чтобы дать возможность явного описания в терминах основных математических выражений. Эти точные решения играют ключевую роль при построении общерелятивистских моделей физических ситуаций. Однако общая теория относительности - это полностью ковариантный теория - ее законы одинаковы, независимо от которых координаты выбираются для описания данной ситуации. Одно прямое следствие состоит в том, что два явно разных точных решения могут соответствовать одной и той же модели вселенной и различаться только своими координатами. Элерс начал искать удобные способы описания точных решений. неизменно, то есть способами, не зависящими от выбора координат. Для этого он исследовал способы описания внутренних геометрических свойств известных точных решений.[15]

    В течение 1960-х годов, продолжая свою докторскую диссертацию, Элерс опубликовал серию статей, все, кроме одной, в сотрудничестве с коллегами из гамбургской группы, которая позже стала известна как «Гамбургская Библия».[16]Первая статья, написанная с Джорданом и Кундтом, представляет собой трактат о том, как систематически характеризовать точные решения полевых уравнений Эйнштейна. Представленный там анализ использует инструменты из дифференциальная геометрия такой как Классификация Петрова из Тензоры Вейля (то есть те части Тензор Римана описывая кривизна из пространство-время которые не связаны уравнениями Эйнштейна), группы изометрий и конформный трансформации. Эта работа также включает первое определение и классификацию pp-волны, класс простых гравитационных волн.[17]

    Следующие статьи этой серии были трактатами по гравитационное излучение (один с Sachs, один с Trümper). Работа с исследованиями Сакса, среди прочего, вакуумные решения с особым алгебраический свойства, используя 2-компонентный спинор формализм. Он также дает систематическое описание геометрических свойств пучков (в математических терминах: конгруэнций) световых лучей. Геометрия пространства-времени может влиять на распространение света, заставляя их сходиться или расходясь друг с другом, или деформируя поперечное сечение пучка без изменения его площади. В статье эти возможные изменения в расслоении формализуются в терминах расширения расслоения (сходимость / расхождение), а также скручивания и сдвига (деформация, сохраняющая площадь поперечного сечения), связывая эти свойства с геометрией пространства-времени. Одним из результатов является Теорема Элерса-Сакса описание свойств тени, создаваемой узким лучом света, встречающим непрозрачный объект. Инструменты, разработанные в этой работе, окажутся необходимыми для открытия Рой Керр его Решение Керра, описывая вращающийся черная дыра - одно из важнейших точных решений.[18]

    Последняя из этих основополагающих статей была посвящена общерелятивистскому подходу к механике сплошных сред. Каким бы полезным ни было понятие точечной массы в классической физике; в общей теории относительности такая идеализированная концентрация массы в одной точке пространства даже не определена четко. Вот почему релятивистские гидродинамика, то есть изучение сплошных сред, является важной частью построения моделей в общей теории относительности. В статье систематически описаны основные концепции и модели, в которых редактор журнала Общая теория относительности и гравитации по случаю публикации перевода на английский язык через 32 года после даты первоначальной публикации, названного «одним из лучших обзоров в этой области».[19]

    Другая часть исследования Элерса точных решений в его диссертации привела к результату, который позже оказался важным. Когда Элерс начал исследования над докторской диссертацией, Золотой век общей теории относительности еще не началось, и основные свойства и концепции черных дыр еще не были поняты. В работе, которая привела к его докторской диссертации, Элерс доказал важные свойства поверхности вокруг черной дыры, которые позже будут идентифицированы как ее горизонт, в частности, что гравитационное поле внутри не может быть статичным, но со временем он должен меняться. Простейшим примером этого является «мост Эйнштейна-Розена», или Червоточина Шварцшильда это часть решения Шварцшильда, описывающего идеализированную сферически-симметричную черную дыру: внутри горизонта находится мостообразное соединение, которое со временем меняется, разрушаясь достаточно быстро, чтобы любой космический путешественник не мог пройти через червоточину.[20]

    Группа Элерс

    Основная статья: Группа Элерс

    В физике двойственность означает, что существуют два эквивалентных описания конкретной физической ситуации с использованием различных физических концепций. Это частный случай физического симметрия, то есть изменение, которое сохраняет ключевые особенности физической системы. Простым примером двойственности является двойственность электрическое поле E и магнитное поле B электродинамика: При полном отсутствии электрических зарядов замена E –B, B E листья Уравнения Максвелла инвариантный. Всякий раз, когда конкретная пара выражений для B и E соответствуют законам электродинамики, переключая два выражения и добавляя знак минус к новому B также действительно.[21]

    В своей докторской диссертации Элерс указал на двойственную симметрию между различными компонентами метрика стационарного вакуум пространство-время, который переводит решения уравнений поля Эйнштейна в другие решения. Эта симметрия между tt-компонентом метрики, которая описывает время, измеряемое часами, пространственные координаты которых не меняются, и термином, известным как потенциал скручивания аналогично упомянутой выше двойственности между E и B.[22]

    Двойственность, открытая Элерсом, была позже расширена до большей симметрии, соответствующей специальная линейная группа . Это больше группа симметрии с тех пор стал известен как Группа Элерс. Его открытие привело к дальнейшим обобщениям, в частности к бесконечномерным Группа Герох (группа Героха порождается двумя не ездящий на работу подгруппы, одна из которых - группа Элерса). Эти так называемые скрытые симметрии играют важную роль в Редукция Калуцы – Клейна как общей теории относительности, так и ее обобщений, таких как одиннадцатимерный супергравитация. Другие приложения включают их использование в качестве инструмента для открытия ранее неизвестных решений и их роль в доказательстве того, что решения в стационарной осесимметричный дело формируют интегрируемая система.[23]

    Космология: теорема Элерса – Герена – Сакса

    Основная статья: Теорема Элерса – Герена – Сакса.
    Неоднородности температуры космического фонового излучения, зарегистрированные на этом изображении со спутникового зонда WMAP составляют не более 10−4 кельвины.

    Теорема Элерса-Герен-Сакса, опубликованная в 1968 году, показывает, что в данной вселенной, если все свободно падающие наблюдатели измеряют космический фон иметь одинаковые свойства во всех направлениях (то есть они измеряют фоновое излучение, чтобы изотропный ), то эта Вселенная является изотропной и однородной Фридман-Лемэтр пространство-время.[24] Космическая изотропия и однородность важны, поскольку они являются основой современной стандартной модели космологии.[25]

    Основные понятия общей теории относительности

    В 1960-х Элерс сотрудничал с Феликс Пирани и Альфред Шильд на конструктивно-аксиоматическом подходе к общей теории относительности: способ вывести теорию из минимального набора элементарных объектов и набора аксиом, определяющих свойства этих объектов. Основными составляющими их подхода являются примитивные концепции, такие как мероприятие, свет луч частица и свободно падающая частица. Вначале пространство-время - это просто набор событий без какой-либо дополнительной структуры. Они постулировали основные свойства света и свободно падающих частиц как аксиомы и с их помощью построили дифференциальная топология, конформная структура и, наконец, метрика структура пространства-времени, то есть: представление о том, когда два события находятся рядом друг с другом, роль световых лучей в связывании событий и понятие расстояния между событиями. Ключевые этапы построения соответствуют идеализированным измерениям, таким как стандартный поиск дальности, используемый в радар. На последнем этапе уравнения Эйнштейна были выведены на основе самого слабого набора дополнительных аксиом. В результате получилась формулировка, которая четко определяет допущения, лежащие в основе общей теории относительности.[26]

    В 1970-х годах в сотрудничестве с Эккартом Рудольфом Элерс обратился к проблеме твердых тел в общей теории относительности. Твердые тела - фундаментальное понятие классической физики. Однако тот факт, что по определению их разные части движутся одновременно, несовместим с релятивистской концепцией скорость света в качестве предельной скорости распространения сигналов и других воздействий. А еще в 1909 г. Макс Борн дал определение жесткости, которое было совместимо с релятивистской физикой, его определение зависит от предположений, которые не выполняются в общем пространстве-времени, и, таким образом, являются чрезмерно ограничительными. Элерс и Рудольф обобщили определение Борна до более приемлемого определения, которое они назвали «псевдожесткостью», которое представляет собой более удовлетворительное приближение к жесткости классической физики.[27]

    Гравитационное линзирование

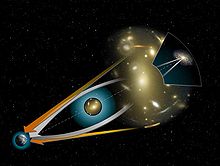
    В большинстве астрофизических моделей систем гравитационных линз используется квазиньютоновское приближение.

    Вместе с Питером Шнайдером Элерс приступил к глубокому изучению основ гравитационное линзирование. Одним из результатов этой работы стала монография 1992 года, написанная в соавторстве с Шнайдером и Эмилио Фалько. Это было первое систематическое изложение темы, которое включало как теоретические основы, так и результаты наблюдений. С точки зрения астрономии, гравитационное линзирование часто описывается с помощью квазиньютоновского приближения - в предположении гравитационное поле быть маленькими, а углы отклонения - минимальными - чего вполне достаточно для большинства ситуаций, имеющих астрофизическое значение. В отличие от этого, монография разработала подробное и полное описание гравитационного линзирования с полностью релятивистской пространственно-временной точки зрения. Эта особенность книги сыграла важную роль в ее долгосрочном положительном восприятии.[28] В последующие годы Элерс продолжил свои исследования распространения пучков света в произвольных пространствах-временах.[29]

    Теория рамок и ньютоновская гравитация

    Основной вывод ньютоновского предела общей теории относительности так же стара, как и сама теория. Эйнштейн использовал его для получения прогнозов, таких как аномальная прецессия перигелия планеты Меркурий. Позже работа Эли Картан, Курт Фридрихс и другие показали более конкретно, как геометрическое обобщение Теория гравитации Ньютона известный как Теория Ньютона – Картана можно понимать как (вырожденный) предел общая теория относительности. Для этого требовалось, чтобы конкретный параметр перейти к нулю. Элерс расширил эту работу, разработав теория фреймов это позволило построить предел Ньютона – Картана, причем математически точно, не только для физических законов, но и для любого пространства-времени, подчиняющегося этим законам (то есть решений уравнений Эйнштейна). Это позволило физикам изучить, что означает ньютоновский предел в конкретных физических ситуациях. Например, теория фреймов может использоваться, чтобы показать, что ньютоновский предел Черная дыра Шварцшильда это простой точечная частица. Кроме того, он позволяет использовать ньютоновские версии точных решений, таких как Модели Фридмана – Леметра. или Вселенная Гёделя быть построенным.[30] С момента своего создания идеи, представленные Элерсом в контексте его теории фреймов, нашли важные приложения в исследовании как ньютоновского предела общей теории относительности, так и теории относительности. Постньютоновское расширение, где ньютоновская гравитация дополняется членами все более высокого порядка по чтобы учесть релятивистские эффекты.[31]

    Общая теория относительности нелинейный: гравитационное влияние двух масс - это не просто сумма индивидуальных гравитационных влияний этих масс, как это было в случае ньютоновской гравитации. Элерс участвовал в обсуждении того, как обратная реакция гравитационного излучения на излучающую систему можно было бы систематически описать в нелинейной теории, такой как общая теория относительности, указав, что стандартная квадруполь формула для потока энергии для таких систем, как двойной пульсар не был (пока) строго выведен: априори вывод требовал включения членов более высокого порядка, чем обычно предполагалось, более высоких, чем рассчитывались до того момента.[32]

    Его работа о ньютоновском пределе, особенно в отношении космологический решений, привели Элерса вместе со своим бывшим докторантом Томасом Бухертом к систематическому исследованию возмущения и неоднородности в ньютоновском космосе. Это заложило основу для более позднего обобщения Бухертом такой трактовки неоднородностей. Это обобщение было основой его попытки объяснить то, что в настоящее время рассматривается как космические эффекты космологическая постоянная или, говоря современным языком, темная энергия, как нелинейное следствие неоднородностей в общерелятивистской космологии.[33]

    История и философия физики

    В дополнение к своему интересу к основам общей теории относительности и, в более общем плане, физики, Элерс исследовал историю физики. Вплоть до своей смерти он участвовал в проекте по истории квантовой теории в Институт истории науки Макса Планка в Берлине.[34] В частности, он исследовал плодотворный вклад Паскуаля Джордана в развитие квантовая теория поля между 1925 и 1928 гг.[35] На протяжении своей карьеры Элерс интересовался философскими основами и значениями физики и вносил свой вклад в исследования по этой теме, обращаясь к таким вопросам, как базовый статус научных знаний в физике.[36]

    Популяризация науки

    Элерс проявлял большой интерес к широкой аудитории. Он часто выступал с публичными лекциями в университетах, а также на таких мероприятиях, как Урания в Берлин. Он был автором научно-популярных статей, в том числе статей в журналах для широкой аудитории, таких как Bild der Wissenschaft. Он редактировал сборник статей о гравитации для немецкого издания Scientific American.[37]Элерс напрямую обращался к учителям физики в своих беседах и журнальных статьях о преподавании теории относительности и связанных с ней основных идей, таких как математика как язык физики.[38]

    Почести и награды

    Элерс стал членом Берлинско-Бранденбургская академия наук и гуманитарных наук (1993), Akademie der Wissenschaften und der Literatur, Майнц (1972), Леопольдина в Галле (1975) и Баварская академия наук и гуманитарных наук в Мюнхене (1979).[39] С 1995 по 1998 год он занимал пост президента Международное общество общей теории относительности и гравитации.[40] Он также получил 2002 Медаль Макса Планка из Немецкое физическое общество, то Вольта Золотая медаль Университет Павии (2005) и медалью факультета естественных наук г. Карлов университет, Прага (2007).[41]

    В 2008 году Международное общество общей теории относительности и гравитации учредило премию Юргена Элерса за диссертацию в память об Элерсе. Его спонсирует научное издательство. Springer и награждается раз в три года на международной конференции общества за лучшую докторскую диссертацию в области математической и числовой общей теории относительности.[42] Выпуск 9 тома 41 журнала Общая теория относительности и гравитации был посвящен Элерсу в память.[43]

    Избранные публикации

    • Börner, G .; Элерс, Дж., Ред. (1996), Гравитация, Spektrum Akademischer Verlag, ISBN  3-86025-362-X
    • Элерс, Юрген (1973), «Обзор общей теории относительности», в Израиле, Вернер (ред.), Относительность, астрофизика и космология, D. Reidel, стр. 1–125, ISBN  90-277-0369-8
    • Schneider, P .; Ehlers, J .; Фалько, Э. Э. (1992), Гравитационные линзы, Спрингер, ISBN  3-540-66506-4

    Примечания

    1. ^ Диссертация Элерс 1957; ср. Эллис 2009.
    2. ^ Schücking, Engelbert (2006), "Jürgen Ehlers", в Schmidt, Bernd G. (ed.), Уравнения поля Эйнштейна и их физические последствия, Springer, стр. V – VI, ISBN  3-540-67073-4
    3. ^ Как описано в Эллис и Красински 2007 и Сакс 2009.
    4. ^ Эллис 2009
    5. ^ Хьюскен, Николай и Шютц 2009, ср. английская версия онлайн как Хьюскен, Николай и Шютц 2008, и соответствующее резюме, Lebenslauf von Prof. Dr. Jürgen Ehlers (PDF), Институт гравитационной физики Макса Планка, 27 мая 2008 г., архивировано из оригинал (PDF) 19 мая 2009 г., получено 2008-05-27 (на немецком, английский перевод названия: «Резюме профессора доктора Юргена Элерса»). Даты и должности также указаны в Вебер и Бориссофф 1998.
    6. ^ Хеннинг и Каземи 2011, п. 472
    7. ^ Хеннинг и Каземи 2011, п. 634
    8. ^ Как описано в Брейер 2008
    9. ^ Брейер 2008
    10. ^ Хеннинг и Каземи 2011, п. 676
    11. ^ Хеннинг и Каземи 2011, п. 737
    12. ^ См. Стр. 520 в годовом отчете Общества Макса Планка за 2000 год, Ярбух 2000, Max-Planck-Gesellschaft, 2000. Время как заслуженное и смерть ср. Браун 2008.
    13. ^ Хьюскен, Николай и Шютц 2009; Английская версия онлайн как Хьюскен, Николай и Шютц 2008
    14. ^ Schücking 2000
    15. ^ Б. Шмидт, Предисловие к Шмидт 2000
    16. ^ Эллис 2009, п. 2180
    17. ^ Более поздняя версия этой статьи Элерс и Кундт, 1962 г. Для оценки см. J. Bicak, p. 14f. в Шмидт 2000
    18. ^ Теорема Элерса-Сакса см. Разд. 5,3 дюйма Фролов и Новиков 1998. Оценка работы и ее связи с решением Керра дана Дж. Бичаком на с. 14f. из Шмидт 2000. Оригинальная работа с Sachs Jordan, Ehlers & Sachs, 1961 г..
    19. ^ Английский перевод, сделанный Г. Ф. Р. Эллис, является Элерс 1993. Цитату можно найти на стр. 1225 в разделе комментариев редактора.
    20. ^ Меняющиеся взгляды на то, что в конечном итоге будет считаться черными дырами, можно найти в Израиль 1987. Тезис Элерса Элерс 1957.
    21. ^ Оливковый 1996
    22. ^ Ср. Доклад Дитера Мэйсона «Двойственность и скрытые симметрии в теориях гравитации», стр. 273–323 в Шмидт 2000.
    23. ^ Maison op. соч., Герох 1971, а для различных приложений Марс 2001.
    24. ^ Хокинг и Эллис 1973, п. 351ff. Оригинальная работа Элерс, Герен и Сакс, 1968 г..
    25. ^ Например. Liddle 2003, стр.2
    26. ^ Видеть Элерс, Пирани и Шильд, 1972 г.; резюме можно найти в Элерс 1973.
    27. ^ Видеть Келер и Шаттнер, 1979 г.. Оригинальная публикация Элерс и Рудольф 1977.
    28. ^ Обзор самой книги есть Блейер 1993. О долгосрочном воздействии можно судить по тому, как на него ссылаются в обзорах более поздних книг по той же теме, например Перлик 2005 и Бозза 2005; см. также оценку Trümper 2009, п. 154.
    29. ^ Зейтц, Шнайдер и Элерс, 1994 г., ср. раздел 3.5 Годовой отчет 1994, Институт астрофизики Макса Планка, 1995, архив из оригинал на 2009-05-19
    30. ^ Элерс 1997; описание можно найти на стр. 216f. в статье Люка Бланше «Постньютоновское гравитационное излучение», стр. 225–271 в Шмидт 2000.
    31. ^ Олийнык и Шмидт 2009
    32. ^ Описание, включающее исторический контекст, можно найти в Schutz 1996. Оригинальная работа Ehlers et al. 1976 г..
    33. ^ Видеть Бухерт и Элерс 1993, Buchert & Ehlers 1997a и Buchert & Ehlers 1997b. Текущее состояние дальнейшей работы Бухерта кратко изложено в Бухерт 2008.
    34. ^ Ср. Браун 2008. Подробности о проекте можно найти на его интернет сайт.
    35. ^ Элерс 2007
    36. ^ Видеть Элерс 2006a и Брейер и Спрингер 2001 а также его более поздний английский перевод Брейер и Спрингер, 2009 г., а также Элерс 2005.
    37. ^ Публичные лекции: Двухгодичный отчет 2004/2005 (PDF), Институт гравитационной физики Макса Планка, 2006 г., архив: оригинал (PDF) на 2007-06-11, перечисляет 25 популярных выступлений (стр. 158f.) только за этот период. Сборник статей Börner & Ehlers 1996, перечислен в Избранные публикации. Пример популярной статьи: Ehlers & Fahr 1994.
    38. ^ Двухгодичный отчет 2004/2005 (PDF), Институт гравитационной физики Макса Планка, 2006 г., архив: оригинал (PDF) на 2007-06-11 перечисляет 11 бесед с учителями или в междисциплинарной среде (стр. 147f., стр. 154f.). Математика и физика Элерс 2006b
    39. ^ Берлин: Хьюскен, Николай и Шютц 2009; дата первоначального членства в краткой записи на стр. 35 той же публикации. Майнц: стр. 13 из Лютьен-Дреколл 2008. Леопольдина: внесена в список Mitgliederverzeichnis, Deutsche Akademie der Naturforscher Leopoldina, получено 2012-05-28 (на немецком, английском переводе названия: Список участников). Баварская академия: Trümper 2009.
    40. ^ История общества GRG, Международное общество общей теории относительности и гравитации, получено 2013-05-28.
    41. ^ Медаль Макса Планка: пресс-релиз о наградах 2002 г., Physikalische Spitzenleistung, Deutsche Physikalische Gesellschaft, 17 декабря 2001 г., архивировано из оригинал 13 февраля 2007 г., получено 27 мая, 2008 (на немецком, английском переводе названия: Высшее достижение по физике), и Рогала 2001. Медаль Вольта: "Имя: профессор д-р Юрген Элерс", Berliner Zeitung, 18 мая 2005 г., получено 2008-05-27 (на немецком языке) и "Medaille für Golmer Forscher", Märkische Allgemeine Zeitung, 19 мая 2005 г. (на немецком, английском переводе названия: Медаль исследователю из Голма). Медаль Карлова университета: Trümper 2009, п. 154.
    42. ^ Премия Юргена Элерса за диссертацию, Сайт Международного общества общей теории относительности и гравитации, получено 2013-05-28
    43. ^ Николай, Эллис и Шмидт, 2009 г.

    Рекомендации

    внешняя ссылка