Плоский модуль - Flat module - Wikipedia

В гомологическая алгебра и алгебраическая геометрия, а плоский модуль через звенеть р является р-модуль M так что принимая тензорное произведение над р с M сохраняет точные последовательности. Модуль - это точно плоский если взятие тензорного произведения с последовательностью дает точную последовательность тогда и только тогда, когда исходная последовательность точна.

Плоскостность была введена Серр  (1956 ) в своей статье Géometrie Algébrique et Géométrie Analytique. Смотрите также плоский морфизм.

Определение

Модуль M над кольцом р называется плоский если выполняется условие: для любого инъективного отображения ${\displaystyle \phi :K\to L}$ из р-модули, карта

${\displaystyle K\otimes _{R}M\to L\otimes _{R}M}$

индуцированный ${\displaystyle k\otimes m\mapsto \phi (k)\otimes m}$ инъективно.

Другими словами, для р-модули K, L, и J, если ${\displaystyle 0\rightarrow K\rightarrow L\rightarrow J\rightarrow 0}$ короткая точная последовательность, то M плоский модуль над р если и только если ${\displaystyle 0\rightarrow K\otimes _{R}M\rightarrow L\otimes _{R}M\rightarrow J\otimes _{R}M\rightarrow 0}$ также короткая точная последовательность.

Это определение применяется также, если р не обязательно коммутативен, и M левый р-модуль и K и L верно р-модули. Единственная разница в том, что в этом случае ${\displaystyle K\otimes _{R}M}$ и ${\displaystyle L\otimes _{R}M}$ не в целом р-модули, а только абелевы группы.

Характеристики плоскостности

Поскольку тензор с M есть для любого модуля M, точный правый функтор

${\displaystyle {\textbf {Mod}}_{R}\to {\textbf {Ab}}}$

(между категорией р-модули и абелевы группы), M плоский тогда и только тогда, когда предыдущий функтор точный.

Это также может быть показано в условии, определяющем плоскостность, как указано выше, достаточно взять ${\displaystyle L=R}$, само кольцо и ${\displaystyle K}$ конечно порожденный идеальный из р.

Плоскостность также эквивалентна следующему условию уравнения, которое можно перефразировать, сказав, что р-линейные отношения, которые сохраняются M вытекают из линейных соотношений, которые сохраняются в р: для каждой линейной зависимости, ${\displaystyle r^{T}x=\sum _{i=1}^{k}r_{i}x_{i}=0}$ с ${\displaystyle r_{i}\in R}$ и ${\displaystyle x_{i}\in M}$, существует матрица ${\displaystyle A\in R^{k\times j}}$ и элемент ${\displaystyle y\in M^{j}}$ такой, что ${\displaystyle Ay=x}$ и ${\displaystyle r^{T}A=0.}$^[1] Более того, M является плоским тогда и только тогда, когда выполняется следующее условие: для каждой карты ${\displaystyle f:F\to M,}$ куда ${\displaystyle F}$ является конечно порожденным свободным ${\displaystyle R}$-модуля, и для каждого конечно порожденного ${\displaystyle R}$-подмодуль ${\displaystyle K}$ из ${\displaystyle \ker f,}$ карта ${\displaystyle f}$ факторы через карту грамм к свободному ${\displaystyle R}$-модуль ${\displaystyle G}$ такой, что ${\displaystyle g(K)=0:}$

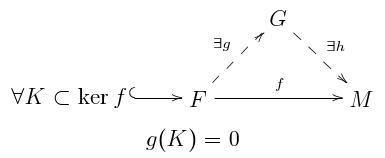
Примеры и отношения к другим понятиям

Плоскостность связана с различными другими условиями на модуле, такими как свободный, проективный или свободный от кручения. Это частично показано на следующем рисунке:

Свободные или проективные модули против плоских модулей

Бесплатные модули плоские над любым кольцом р. Это верно, поскольку функтор

${\displaystyle L\mapsto L\otimes _{R}(\bigoplus _{i\in I}R)\cong \bigoplus _{i\in I}L}$

точно. Например, векторные пространства через поле плоские модули. Прямые слагаемые плоских модулей снова плоские. Особенно, проективные модули (прямые слагаемые свободных модулей) плоские. Наоборот, для коммутативной Кольцо Нётериана р, конечно порожденный плоские модули проективны.

Плоские модули против модулей без кручения

Любой плоский модуль без кручения. Обратное верно для целых чисел и в более общем случае для области главных идеалов. Это следует из приведенной выше характеристики плоскостности в терминах идеалов. Но в более общем смысле это обратное Кольца дедекинда.

Область целостности называется Прюфер домен если каждый модуль без кручения над ним плоский.

Плоскостность завершений

Позволять ${\displaystyle A}$ быть нётеровым кольцом и ${\displaystyle I}$ идеальный. Тогда завершение ${\displaystyle A\to {\widehat {A}}}$ относительно ${\displaystyle I}$ плоский.^[2] Он действительно плоский тогда и только тогда, когда ${\displaystyle I}$ содержится в радикале Джекобсона ${\displaystyle A}$.^[3] (ср. Кольцо Зарисского.)

Не примеры

Частные плоские модули, как правило, не плоские. Например, для каждого целого числа ${\displaystyle n>1,\mathbb {Z} /n\mathbb {Z} }$ не плоский ${\displaystyle \mathbb {Z} ,}$ потому что ${\displaystyle n:\mathbb {Z} \to \mathbb {Z} ,x\mapsto nx}$ является инъективным, но тензором с ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ это не так. По аналогии, ${\displaystyle \mathbb {Q} /\mathbb {Z} }$ не плоский ${\displaystyle \mathbb {Z} .}$

Другие свойства постоянства

В общем, произвольные прямые суммы и отфильтрованные копределы (также известен как прямые ограничения ) плоских модулей являются плоскими, что является следствием того факта, что тензорное произведение коммутирует с прямыми суммами и фильтрованными копределами (фактически со всеми копределы ), и что прямые суммы и фильтрованные копределы равны точные функторы. В частности, это показывает, что все фильтрованные копределы свободных модулей плоские.

Лазар (1969) доказал, что верно и обратное: M плоский тогда и только тогда, когда это прямой предел из конечно порожденный бесплатные модули. Как следствие, можно сделать вывод, что каждый конечно представленный плоский модуль проективен. прямая сумма ${\displaystyle \bigoplus \nolimits _{i\in I}M_{i}}$ плоский тогда и только тогда, когда каждый ${\displaystyle M_{i}}$ плоский.

Товары квартиры р-модули не обязательно должны быть плоскими. Фактически, Чейз (1960) показал кольцо р является последовательный (т.е. любой конечно порожденный идеал конечно определен) тогда и только тогда, когда произвольные произведения плоских р-модули снова плоские.^[4]

Удлинители плоских колец

Если ${\displaystyle \phi :R\to S}$ - гомоморфизм колец, S называется плоской р (или квартира р-алгебра), если она плоская как р-модуль. Например, кольцо многочленов р[т] плоско р, для любого кольца р. Причем для любого мультипликативно замкнутое подмножество ${\displaystyle S}$ коммутативного кольца ${\displaystyle R}$, то кольцо локализации ${\displaystyle S^{-1}R}$ плоский р. Например, ${\displaystyle \mathbb {Q} }$ плоский ${\displaystyle \mathbb {Z} }$ (хотя и не проективный).

Позволять ${\displaystyle S=R[x_{1},\dots ,x_{r}]}$ кольцо многочленов над нётеровым кольцом ${\displaystyle R}$ и ${\displaystyle f\in S}$ ненулевой делитель. потом ${\displaystyle S/fS}$ плоский ${\displaystyle R}$ если и только если ${\displaystyle f}$ является примитивный (коэффициенты образуют единичный идеал).^[5] Это дает пример платного плоского модуля.

Кунц (1969) показал, что нётерское местное кольцо ${\displaystyle R}$ положительных характеристика п является обычный если и только если Морфизм Фробениуса ${\displaystyle R\to R,r\mapsto r^{p}}$ плоский и ${\displaystyle R}$ является уменьшенный.

Расширения плоских колец важны в алгебре, алгебраической геометрии и смежных областях. Морфизм ${\displaystyle f:X\to Y}$ из схемы это плоский морфизм если по одному из нескольких эквивалентных определений индуцированное отображение на локальных кольцах

${\displaystyle {\mathcal {O}}_{Y,f(x)}\to {\mathcal {O}}_{X,x}}$

является гомоморфизмом плоских колец для любой точки Икс в Икс. Таким образом, упомянутые выше свойства плоских (или строго плоских) морфизмов, установленные методами коммутативной алгебры, переводятся в геометрические свойства плоских морфизмов в алгебраической геометрии.

Локальные аспекты плоскостности над коммутативными кольцами

В этом разделе кольцо р предполагается коммутативным. В этой ситуации плоскостность р-modules связано с понятием локализация: M плоский тогда и только тогда, когда модуль ${\displaystyle M_{\mathfrak {p}}}$ это квартира ${\displaystyle R_{\mathfrak {p}}}$-модуль для всех главные идеалы ${\displaystyle {\mathfrak {p}}}$ из р. Фактически, достаточно проверить последнее условие только для максимальные идеалы, в отличие от всех основных идеалов. Это утверждение сводит вопрос о плоскостности к случаю (коммутативных) локальных колец.

Если р является локальным (коммутативным) кольцом и либо M конечно порожден или максимальный идеал р нильпотентен (например, артистическое местное кольцо ), то стандартная импликация "свободный означает плоский" может быть изменена: в этом случае M плоский тогда и только тогда, когда он свободен.^[6]

В локальный критерий плоскостности состояния:^[7]

Позволять р быть местным нётерским кольцом, S местный нётер р-алгебра с ${\displaystyle {\mathfrak {m}}_{R}S\subset {\mathfrak {m}}_{S}}$, и M конечно порожденный S-модуль. потом M плоский р если и только если ${\displaystyle \operatorname {Tor} _{1}^{R}(M,R/{\mathfrak {m}}_{R})=0.}$

Значение этого в том, что S не обязательно быть конечным по р и нам нужно только рассмотреть максимальный идеал р вместо произвольного идеала р.

Следующий критерий также полезен для проверки плоскостности:^[8]

Позволять р, S быть как в локальном критерии плоскостности. Предполагать S является Коэн – Маколей и р является обычный. потом S плоский р если и только если ${\displaystyle \dim S=\dim R+\dim S/{\mathfrak {m}}_{R}S.}$

Точно плоский гомоморфизм колец

Позволять А кольцо (в этом разделе предполагается коммутативным) и B ан А-алгебра, т. е. кольцевой гомоморфизм ${\displaystyle f:A\to B}$. потом B имеет структуру А-модуль. потом B говорят, что он плоский А (соответственно точно плоский над А), если он плоский (или точно плоский) как А-модуль.

Существует основная характеристика строго плоского гомоморфизма колец: задан плоский гомоморфизм колец ${\displaystyle f:A\to B}$, следующие эквивалентны.

1. ${\displaystyle f}$ точно плоский.
2. Для каждого максимального идеала ${\displaystyle {\mathfrak {m}}}$ из ${\displaystyle A}$, ${\displaystyle {\mathfrak {m}}B\neq B.}$
3. Если ${\displaystyle N\neq 0}$ ненулевой ${\displaystyle A}$-модуль, затем ${\displaystyle N\otimes _{A}B\neq 0.}$
4. Каждый главный идеал А это прообраз под ж главного идеала в B. Другими словами, индуцированное отображение ${\displaystyle f^{*}:\operatorname {Spec} (B)\to \operatorname {Spec} (A)}$ сюръективно.
5. А это чистое подкольцо из B (в частности, подкольцо); здесь "чистое подкольцо" означает, что ${\displaystyle N\to N\otimes _{A}B}$ инъективен для каждого ${\displaystyle A}$-модуль ${\displaystyle N}$.^[9]

Из условия 2 следует, что плоский локальный гомоморфизм между локальными кольцами строго плоский. Из условия 5 следует, что ${\displaystyle I=IB\cap A}$ для каждого идеала ${\displaystyle I\subset A}$ (брать ${\displaystyle N=A/I}$); в частности, если ${\displaystyle B}$ является нётеровым кольцом, то ${\displaystyle A}$ является нётеровым кольцом.

Условие 4 можно сформулировать в следующей усиленной форме: ${\displaystyle \operatorname {Spec} (B)\to \operatorname {Spec} (A)}$ является погружающийся: топология ${\displaystyle \operatorname {Spec} (A)}$ это факторная топология из ${\displaystyle \operatorname {Spec} (B)}$ (это частный случай того, что точно плоский квазикомпактный морфизм схем обладает этим свойством.^[10]) По сравнению с интегральное расширение интегрально замкнутой области. Смотрите также плоский морфизм # Свойства плоских морфизмов для дополнительной информации.

Вот одна характеристика строго плоского гомоморфизма для необязательно плоского гомоморфизма. Учитывая инъективный локальный гомоморфизм ${\displaystyle (A,{\mathfrak {m}})\hookrightarrow (B,{\mathfrak {n}})}$ такой, что ${\displaystyle {\mathfrak {m}}B}$ является ${\displaystyle {\mathfrak {n}}}$-первоначальный идеал, ${\displaystyle A\to B}$ действительно плоский тогда и только тогда, когда теорема перехода держится за это; т.е. для каждого ${\displaystyle {\mathfrak {m}}}$-первоначальный идеал ${\displaystyle Q}$ из ${\displaystyle A}$, ${\displaystyle \operatorname {length} _{B}(B/QB)=\operatorname {length} _{B}(B/{\mathfrak {m}}B)\operatorname {length} _{A}(A/Q).}$^[11]

Пример. Для кольца ${\displaystyle A,A\to A[x]}$ точно плоский. В более общем плане ${\displaystyle A}$-алгебра свободный положительного ранга как ${\displaystyle A}$-модуль абсолютно плоский. Так, например, для монического многочлена ${\displaystyle f\in A[t]}$, включение ${\displaystyle A\hookrightarrow A[t]/(f)}$ точно плоский.

Пример. Позволять ${\displaystyle A}$ быть кольцом и ${\displaystyle f_{1},\ldots ,f_{r}}$ элементы в нем. Затем эти элементы создают единичный идеал ${\displaystyle (1)}$ из ${\displaystyle A}$ если и только если

${\displaystyle A\to B=\prod _{i}A[f_{i}^{-1}]}$

строго плоская, поскольку локализации плоские, их прямые суммы тогда плоские и

${\displaystyle \operatorname {Spec} B=\bigcup _{i}\operatorname {Spec} A[f_{i}^{-1}]\to \operatorname {Spec} A}$

сюръективен тогда и только тогда, когда элементы порождают единичный идеал.^[12]

Для данного гомоморфизма колец ${\displaystyle f:A\to B,}$ есть связанный комплекс, называемый Амицур комплекс:^[13]

${\displaystyle 0\to A{\overset {f}{\to }}B{\overset {\delta ^{0}}{\to }}B\otimes _{A}B{\overset {\delta ^{1}}{\to }}B\otimes _{A}B\otimes _{A}B\to \cdots }$

где кограничные операторы ${\displaystyle \delta ^{n}}$ - чередующиеся суммы карт, полученные путем вставки 1 в каждое пятно; например., ${\displaystyle \delta ^{0}(b)=b\otimes 1-1\otimes b}$. Тогда (Гротендик) этот комплекс точен, если ${\displaystyle f}$ точно плоский.

Гомологическая характеризация с помощью функторов Tor

Плоскостность также можно выразить с помощью Функторы Tor, то левые производные функторы тензорного произведения. Левый р-модуль M плоский тогда и только тогда, когда

${\displaystyle \operatorname {Tor} _{n}^{R}(X,M)=0}$ для всех ${\displaystyle n\geq 1}$ и хорошо р-модули Икс).^[14]

Фактически, достаточно проверить, что первый член Tor обращается в нуль, т.е. M плоский тогда и только тогда, когда

${\displaystyle \operatorname {Tor} _{1}^{R}(N,M)=0}$

для любого р-модуль N или, что еще более ограничительно, когда ${\displaystyle N=R/I}$ и ${\displaystyle I\subset R}$ - любой конечно порожденный идеал.

Использование функтора Tor длинные точные последовательности, тогда можно легко доказать факты о короткая точная последовательность

${\displaystyle 0\to A{\overset {f}{\longrightarrow }}B{\overset {g}{\longrightarrow }}C\to 0}$

Если А и C плоские, значит, тоже B. Кроме того, если B и C плоские, значит, тоже А. Если А и B плоские, C в целом не обязательно должен быть плоским, как показано в приведенном выше непримере ${\displaystyle \mathbb {Z} /n}$. Однако если А является чистый в B и B плоский, то А и C плоские.

Плоские разрешения

А плоское разрешение модуля M это разрешающая способность формы

${\displaystyle \cdots \to F_{2}\to F_{1}\to F_{0}\to M\to 0,}$

где F_я все плоские модули. Любая свободная или проективная резолюция обязательно является плоской резолюцией. Плоские разрешения можно использовать для вычисления Функтор Tor.

В длина конечного плоского разрешения - это первый индекс п такой, что F_п отличен от нуля и F_я = 0 для я > п. Если модуль M допускает конечное плоское разрешение - минимальную длину среди всех конечных плоских разрешений M называется его плоский размер^[15] и обозначили fd (M). Если M не допускает конечного плоского разрешения, то по соглашению плоская размерность называется бесконечной. В качестве примера рассмотрим модуль M такой, что fd (M) = 0. В этой ситуации точность последовательности 0 → F₀ → M → 0 указывает, что стрелка в центре является изоморфизмом, и, следовательно, M сам по себе плоский.^[16]

В некоторых областях теории модулей плоское разрешение должно удовлетворять дополнительному требованию, чтобы каждая карта была плоским предварительным покрытием ядра карты справа. Для проективных резольвент это условие почти невидимо: проективное предпокрытие - это просто эпиморфизм из проективного модуля. Эти идеи вдохновлены работами Ауслендера в приближении. Эти идеи также знакомы по более распространенному понятию минимальных проективных разрешений, где каждая карта должна быть проективное покрытие ядра карты справа. Однако проективные покрытия в общем случае не должны существовать, поэтому минимальные проективные резольвенты имеют ограниченное применение над кольцами, такими как целые числа.

Плоские крышки

Хотя проективные покрытия для модулей не всегда существуют, предполагалось, что для общих колец каждый модуль будет иметь плоское покрытие, то есть каждый модуль M будет эпиморфным изображением плоского модуля F такое, что каждая карта из плоского модуля на M факторы через F, и любой эндоморфизм F над M это автомобилизм. Этот гипотеза о плоской крышке впервые было явно указано в (Енох 1981, стр 196) ошибка harv: цель отсутствует: CITEREFEnochs1981 (помощь). Гипотеза оказалась верной, положительно разрешенной и доказанной одновременно Л. Биканом, Р. Эль Баширом и Э. Енохом.^[17] Этому предшествовали важные работы П. Эклофа, Дж. Трлифая и Дж. Сюй.

Поскольку плоские покрытия существуют для всех модулей над всеми кольцами, минимальные плоские резольвенты могут заменять минимальные проективные резольвенты во многих случаях. Измерение отклонения плоских разрешений от проективных разрешений называется относительная гомологическая алгебра, и он рассматривается в таких классических произведениях, как (Маклейн 1963 ) ошибка harv: цель отсутствует: CITEREFMacLane1963 (помощь) и в более поздних работах, сосредоточенных на плоских разрешениях, таких как (Енохс и Дженда 2000 ).

В конструктивной математике

Плоские модули имеют повышенное значение в конструктивная математика, где проективные модули менее полезны. Например, то, что все свободные модули проективны, эквивалентно полному аксиома выбора, поэтому теоремы о проективных модулях, даже если они доказаны конструктивно, не обязательно применимы к свободным модулям. Напротив, для доказательства того, что свободные модули плоские, выбора не требуется, поэтому теоремы о плоских модулях все еще применимы.^[18]

Смотрите также

• Общая плоскостность
• Плоский морфизм
• регулярное кольцо фон Неймана - те кольца, над которыми все модули плоские.
• Обычно плоское кольцо

Рекомендации

1. Бурбаки, Гл. I, § 2. Предложение 13, следствие 1. ошибка harvnb: цель отсутствует: CITEREFBourbaki (помощь)
2. Мацумура 1970, Следствие 1 теоремы 55, с. 170
3. Мацумура 1970, Теорема 56
4. «Плоскостность колец Power Series». mathoverflow.net.
5. Эйзенбуд, Упражнение 6.4. ошибка harvnb: цель отсутствует: CITEREFEisenbud (помощь)
6. Мацумура, Предложение 3.G ошибка harvnb: цель отсутствует: CITEREFMatsumura (помощь)
7. Эйзенбуд 1994, Теорема 6.8 Ошибка harvnb: цель отсутствует: CITEREFEisenbud1994 (помощь)
8. Эйзенбуд 1994, Теорема 18.16 Ошибка harvnb: цель отсутствует: CITEREFEisenbud1994 (помощь)
9. Доказательство: предположим ${\displaystyle f:A\to B}$ точно плоский. Для А-модуль N, карта ${\displaystyle B=A\otimes _{A}B\to B\otimes _{A}B}$ экспонаты B как чистое подкольцо и так ${\displaystyle N\otimes _{A}B\to N\otimes _{A}(B\otimes B)\simeq (N\otimes _{A}B)\otimes _{A}B}$ инъективно. Следовательно, ${\displaystyle N\to N\otimes _{A}B}$ инъективно. Наоборот, если ${\displaystyle N\neq 0}$ это модуль над ${\displaystyle A}$, тогда ${\displaystyle 0\neq N\subset N\otimes _{B}A}$.
10. SGA 1, Exposé VIII., Corollay 4.3. ошибка harvnb: цель отсутствует: CITEREFSGA_1 (помощь)
11. Мацумура 1986, Гл. 8, упражнение 22.1.
12. Артин, Упражнение (3) после предложения III.5.2. ошибка harvnb: нет цели: CITEREFArtin (помощь)
13. «Амицур Комплекс». ncatlab.org.
14. Точно так же право р-модуль M плоский тогда и только тогда, когда ${\displaystyle \operatorname {Tor} _{n}^{R}(M,X)=0}$ для всех ${\displaystyle n\geq 1}$ и все осталось р-модули Икс.
15. Лам 1999, п. 183.
16. Модуль, изоморфный плоскому модулю, конечно, плоский.
17. Бикан, Эль Башир и Енохс 2001.
18. Ричман 1997.

• Артин, Майкл (1999). «Некоммутативные кольца» (PDF).
• Bican, L .; Эль Башир, Р .; Энохс, Э. (2001), «Все модули имеют плоские крышки», Бык. Лондонская математика. Soc., 33 (4): 385–390, Дои:10.1017 / S0024609301008104, ISSN  0024-6093, МИСТЕР  1832549
• Н. Бурбаки, Коммутативная алгебра
• Чейз, Стивен У. (1960), "Прямые произведения модулей", Труды Американского математического общества, 97: 457–473, Дои:10.2307/1993382, МИСТЕР  0120260
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра, Тексты для выпускников по математике, 150, Берлин, Нью-Йорк: Springer-Verlag, Дои:10.1007/978-1-4612-5350-1, ISBN  978-0-387-94268-1, МИСТЕР  1322960, ISBN  978-0-387-94269-8
• Енохс, Эдгар Э. (1981), "Инъективные и плоские крышки, конверты и резольвенты", Israel J. Math., 39 (3): 189–209, Дои:10.1007 / BF02760849, ISSN  0021-2172, МИСТЕР  0636889
• Енох, Эдгар Э .; Дженда, Овертаун М. Г. (2000), Относительная гомологическая алгебра, Выставки де Грюйтера по математике, 30, Берлин: Walter de Gruyter & Co., Дои:10.1515/9783110803662, ISBN  978-3-11-016633-0, МИСТЕР  1753146
• Кунц, Эрнст (1969), "Характеризация регулярных локальных колец характеристики п", Американский журнал математики, 91: 772–784, Дои:10.2307/2373351, МИСТЕР  0252389
• Лам, Цит-Юэн (1999), Лекции по модулям и кольцам, Тексты для выпускников по математике № 189, Берлин, Нью-Йорк: Springer-Verlag, Дои:10.1007/978-1-4612-0525-8, ISBN  978-0-387-98428-5, МИСТЕР  1653294
• Лазар, Д. (1969), "Autour de la platitude", Bulletin de la Société Mathématique de France, 97: 81–128
• Мак-Лейн, Сондерс (1963), Гомология, Die Grundlehren der Mathematischen Wissenschaften, Bd. 114, Бостон, Массачусетс: Академическая пресса, МИСТЕР  0156879
• Мацумура, Хидеюки (1970), Коммутативная алгебра
• Мацумура, Хидеюки (1986). Коммутативная теория колец. Кембриджские исследования в области высшей математики. 8. Издательство Кембриджского университета. ISBN  0-521-36764-6. МИСТЕР  0879273. Zbl  0603.13001.
• Мамфорд, Дэвид, Красная книга разновидностей и схем
• Норткотт, Д. Г. (1984), Полилинейная алгебра, Издательство Кембриджского университета, ISBN  978-0-521-26269-9 - стр. 33
• Ричман, Фред (1997), "Плоская размерность, конструктивность и теорема Гильберта о сизигии", Новозеландский математический журнал, 26 (2): 263–273, ISSN  1171-6096, МИСТЕР  1601663
• Серр, Жан-Пьер (1956), "Géométrie algébrique et géométrie analytique", Annales de l'Institut Fourier, 6: 1–42, Дои:10.5802 / aif.59, ISSN  0373-0956, МИСТЕР  0082175