Действительность (логика) - Validity (logic)

В логика, точнее в дедуктивное мышление, аргумент является действительный тогда и только тогда, когда он принимает форму, которая делает невозможным предпосылки быть правдой, а вывод, тем не менее, ложным.^[1] Для действительного аргумента необязательно иметь истинные посылки,^[2] но иметь посылки, которые, если бы они были верны, гарантировали бы истинность вывода аргумента. Веские аргументы должны быть четко выражены с помощью предложений, называемых правильные формулы (также называемый wffs или просто формулы). В срок действия аргумента - его действительность - можно проверить, доказать или опровергнуть, и это зависит от его логическая форма.^[3]

Аргументы

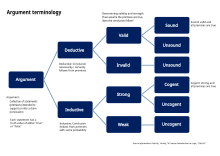
Терминология аргументов, используемая в логике

В логике аргумент набор утверждений, выражающих предпосылки (все, что состоит из эмпирических свидетельств и аксиоматических истин) и доказательно обоснованный вывод.

Аргумент действительный тогда и только тогда, когда вывод будет ложным, если все посылки верны.^[3] Валидность не требует истинности посылок, вместо этого она просто требует, чтобы вывод вытекал из прежних, не нарушая правильности логическая форма. Если также подтверждаются посылки действительного аргумента, то это называется звук.^[3]

В соответствующий условный действительного аргумента является логическая правда а отрицание соответствующего ему условного оператора есть противоречие. Вывод - это логическое следствие своих помещений.

Недействительный аргумент называется «недействительным».

Пример действительного аргумента дается следующим хорошо известным силлогизм:

Все люди смертны.

Сократ - мужчина.

Следовательно, Сократ смертен.

Что делает этот аргумент достоверным, так это не то, что он имеет истинные посылки и истинный вывод, а логическая необходимость заключения, учитывая эти две посылки. Аргумент был бы столь же верным, если бы посылки и заключение были ложными. Следующий аргумент аналогичен логическая форма но с ложными предпосылками и ложным выводом, и это в равной степени верно:

Все чашки зеленые.

Сократ - это чашка.

Следовательно, Сократ зеленый.

Независимо от того, как Вселенная могла быть построена, ни в коем случае не могло быть случая, чтобы эти аргументы имели одновременно истинные предпосылки, но ложное заключение. Приведенные выше аргументы можно противопоставить следующему неверному:

Все люди бессмертны.

Сократ - мужчина.

Следовательно, Сократ смертен.

В этом случае вывод противоречит дедуктивной логике предыдущих посылок, а не вытекает из нее. Следовательно, этот аргумент является логически «недействительным», даже если вывод можно считать «истинным» в общих чертах. Предпосылка «Все люди бессмертны» также была бы признана ложной вне рамок классической логики. Однако внутри этой системы «истина» и «ложь», по сути, больше похожи на математические состояния, такие как двоичные единицы и нули, чем на философские концепции, обычно связанные с этими терминами.

Стандартное представление состоит в том, что то, действителен ли аргумент, зависит от аргумента. логическая форма. Логики используют множество техник для представления логической формы аргумента. Простой пример, примененный к двум из приведенных выше иллюстраций, следующий: пусть буквы «P», «Q» и «S» означают, соответственно, множество людей, множество смертных и Сократа. Используя эти символы, первый аргумент может быть сокращен как:

Все P - Q.

S - это P.

Следовательно, S является Q.

Точно так же второй аргумент становится:

Все P не являются Q.

S - это P.

Следовательно, S является Q.

Аргумент называется формально действительным, если он имеет структурную самосогласованность, т.е.если, когда все операнды между предпосылками верны, производный вывод всегда также верен. В третьем примере исходные посылки не могут логически привести к заключению и поэтому классифицируются как неверный аргумент.

Действительная формула

Формула формальный язык является действительной формулой тогда и только тогда, когда она верна при всех возможных интерпретация языка. В логике высказываний они тавтологии.

Заявления

Утверждение можно назвать достоверным, то есть логической истиной, если оно истинно во всех интерпретациях.

Разумность

На действительность вывода не влияет истинность посылки или истинность вывода. Совершенно верно следующий вывод:

Все животные живут на Марсе.

Все люди животные.

Следовательно, все люди живут на Марсе.

Проблема с аргументом в том, что это не звук. Чтобы дедуктивный аргумент был верным, он должен быть верным и все предпосылки должны быть верными.^[3]

Удовлетворенность

Теория моделей анализирует формулы относительно определенных классов интерпретации в подходящих математических структурах. При таком прочтении формула действительна, если все такие интерпретации подтверждают ее. Вывод действителен, если все интерпретации, подтверждающие посылки, подтверждают вывод. Это известно как семантическая достоверность.^[4]

Сохранение

В сохраняющий истину валидность, интерпретация, при которой всем переменным присваивается значение истины of "true" дает значение истинности "true".

В фальшивый достоверность, интерпретация, при которой всем переменным присваивается значение истинности «ложь», дает значение истинности «ложь».^[5]

Свойства консервации	Логическая связка фразы
Истинное и ложное сохранение:	Предложение • Логическое соединение (И, ${displaystyle land}$ ) • Логическая дизъюнкция (ИЛИ, ${displaystyle lor}$ )
Только истинное сохранение:	Тавтология ( ${displaystyle op}$ ) • Бикондиционный (XNOR, ${displaystyle leftrightarrow}$ ) • Последствия ( ${displaystyle ightarrow}$ ) • Обратное значение ( ${displaystyle leftarrow}$ )
Только ложное сохранение:	Противоречие ( ${displaystyle ot}$ ) • Исключительная дизъюнкция (XOR, ${displaystyle oplus}$ ) • Неимпликация ( ${displaystyle rightarrow}$ ) • Обратное неимпликация ( ${displaystyle leftarrow}$ )
Несохраняющий:	Отрицание ( ${displaystyle eg}$ ) • Альтернативное отрицание (NAND, ${displaystyle uparrow}$ ) • Совместное отрицание (NOR, ${displaystyle downarrow}$ )

Смотрите также

дальнейшее чтение

Барвайз, Джон; Этчменди, Джон. Язык, доказательство и логика (1999): 42.
Пиво, Фрэнсис А. "Валидность: взгляд на политологию ", Социальная эпистемология 7, 1 (1993): 85-105.

[1] Действительность и обоснованность - Интернет-энциклопедия философии

[2] Джей Си Билл и Грег Рестолл, «Логическое следствие», Стэнфордская энциклопедия философии (издание осень 2014 г.).

[:0-3] а ^б ^c ^d Генслер, Гарри Дж., 1945 г. - (6 января 2017 г.). Введение в логику (Третье изд.). Нью-Йорк. ISBN 978-1-138-91058-4. OCLC 957680480.CS1 maint: несколько имен: список авторов (связь)

[4] Л. Т. Ф. Гамут, Логика, язык и смысл: введение в логику, University of Chicago Press, 1991, стр. 115.

[5] Роберт Коган, Критическое мышление: шаг за шагом, University Press of America, 1998 г., п. 48.

[1]

[2]

[3]

[4]

[5]

Математическая логика
Общий	Формальный язык Правило формирования Формальное доказательство Формальная семантика Правильная формула Набор Элемент Учебный класс Классическая логика Аксиома Правило вывода Связь Теорема Логическое следствие Теория типов Символ Синтаксис Теория
Системы	Формальная система Дедуктивная система Аксиоматическая система Системы гильбертовского стиля Естественный вычет Последовательное исчисление
Традиционная логика	Предложение Вывод Аргумент Срок действия Силлогизм Площадь оппозиции Диаграмма Венна
Исчисление высказываний и Логическая логика	Логические функции Исчисление высказываний Пропозициональная формула Логические связки Таблицы истинности Многозначная логика
Логика предикатов	Первый заказ Квантификаторы Предикат Второго порядка Монадическое исчисление предикатов
Наивная теория множеств	Набор Пустой набор Элемент Перечисление Расширяемость Конечный набор Бесконечный набор Подмножество Набор мощности Счетный набор Бесчисленное множество Рекурсивный набор Домен Codomain Изображение карта Функция Связь Упорядоченная пара
Теория множеств	Основы математики Теория множеств Цермело – Френкеля Аксиома выбора Общая теория множеств Теория множеств Крипке – Платека. Теория множеств фон Неймана – Бернейса – Гёделя. Теория множеств Морса – Келли Теория множеств Тарского – Гротендика
Теория моделей	Модель Интерпретация Нестандартная модель Теория конечных моделей Ценность правды Срок действия
Теория доказательств	Формальное доказательство Дедуктивная система Формальная система Теорема Логическое следствие Правило вывода Синтаксис
Вычислимость теория	Рекурсия Рекурсивный набор Рекурсивно перечислимый набор Проблема решения Тезис Черча – Тьюринга Вычислимая функция Примитивная рекурсивная функция