Enneadecagon - Enneadecagon

Обычный эннеадекагон
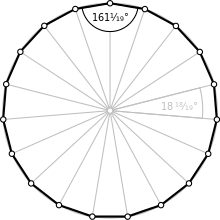Обычный эннеадекагон
Тип	Правильный многоугольник
Края и вершины	19
Символ Шлефли	{19}
Диаграмма Кокстера
Группа симметрии	Двугранный (D19), порядок 2 × 19
Внутренний угол (градусы )	≈161.052°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия ан эннеадекагон или же Enneakaidecagon или 19-угольник - девятнадцатигранный многоугольник.

Обычная форма

А обычный эннеадекагон представлен Символ Шлефли {19}.

Радиус описанный круг из обычный эннеадекагон с длиной стороны т является ${\displaystyle R={\frac {t}{2}}\csc {\frac {180}{19}}}$ (угол в градусах). В площадь, куда т длина ребра, ${\displaystyle {\frac {19}{4}}t^{2}\cot {\frac {\pi }{19}}\simeq 28.4652\,t^{2}.}$

Строительство

Поскольку 19 - это Pierpont Prime но не Ферма Прайм, обычный эннеадекагон не может быть построен используя компас и линейка. Однако его можно построить, используя Neusis, или трехугольник.

Обычный аннеадекагон, точное построение с использованием квадратик по Гиппию в качестве дополнительной помощи

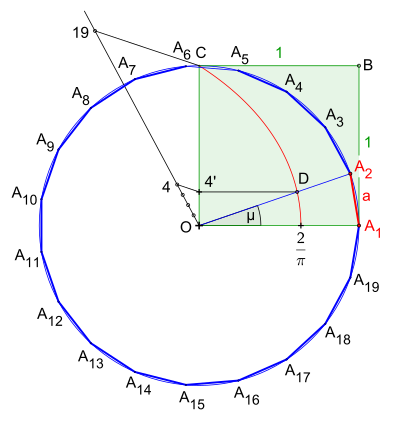
Приблизительный аннеадекагон, вписанный в круг

Еще одна анимация примерного строительства.

Эннеадекагон, примерное построение в виде анимации, с паузой 15 с

На основе единичной окружности r = 1 [единица длины]

• Построенная длина стороны аннеадекагона в GeoGebra ${\displaystyle a=0.329189180561468...\;}$ [единица длины]
• Длина стороны эннеадекагона ${\displaystyle a_{target}=2\cdot \sin \left({\frac {180^{\circ }}{19}}\right)=0.329189180561467788...\;}$[единица длины]
• Абсолютная погрешность построенной длины стороны ${\displaystyle F_{a}=a-a_{target}=2.12...E-16\;}$[единица длины]
• Построенный центральный угол аннеадекагона в GeoGebra ${\displaystyle \mu =18.94736842105263...^{\circ }}$
• Центральный угол аннеадекагона ${\displaystyle \mu _{target}={\frac {360^{\circ }}{19}}=18.947368421052631578...^{\circ }}$
• Абсолютная погрешность построенного центрального угла ${\displaystyle F_{\mu }=\mu -\mu _{target}=-1.578...E-15^{\circ }}$

Пример для иллюстрации ошибки

В радиусе r = 1 млрд км (расстояние, на которое свету потребуется примерно 55 минут), абсолютная погрешность построенной длины стороны будет ок. 0,21 мм.

Симметрия

Симметрии правильного аннеадакагона. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.

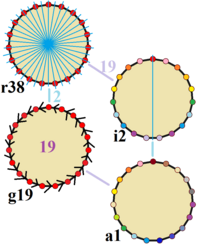
В регулярный эннеадекагон имеет Dih₁₉ симметрия, порядок 38. Так как 19 - это простое число есть одна подгруппа с диэдральной симметрией: Dih₁, и 2 циклическая группа симметрии: Z₁₉, а Z₁.

Эти 4 симметрии можно увидеть в 4 различных симметриях на эннеадекагоне. Джон Конвей маркирует их буквой и групповым порядком.^[1] Полная симметрия правильной формы r38 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров), и я когда линии отражения проходят через ребра и вершины. Циклические симметрии в среднем столбце помечены как грамм для их приказов центрального вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g19 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Связанные полигоны

Эннеадекаграмма - это 19-сторонняя звездный многоугольник. Есть восемь обычных форм, которые дает Символы Шлефли: {19/2}, {19/3}, {19/4}, {19/5}, {19/6}, {19/7}, {19/8} и {19/9}. Поскольку 19 - простое число, все эннеадекаграммы представляют собой правильные звезды, а не составные числа.

Рисунок	{19/2}	{19/3}	{19/4}	{19/5}
Внутренний угол	≈142.105°	≈123.158°	≈104.211°	≈85.2632°
Рисунок	{19/6}	{19/7}	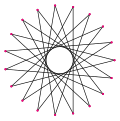{19/8}	{19/9}
Внутренний угол	≈66.3158°	≈47.3684°	≈28.4211°	≈9.47368°

Полигоны Петри

Обычный эннеадекагон - это Многоугольник Петри для одного многомерного многогранника, спроецированного под углом ортогональная проекция:

18-симплекс (18D)

Рекомендации

1. Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN  978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)

• эннеадекагон

внешняя ссылка

• Вайсштейн, Эрик В. "Enneadecagon". MathWorld.