Октаграмма - Octagram
| Обычная октаграмма | |
|---|---|
 Обычная октаграмма | |
| Тип | Правильный звездный многоугольник |
| Края и вершины | 8 |
| Символ Шлефли | {8/3} т {4/3} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D8) |
| Внутренний угол (градусы ) | 45° |
| Двойной многоугольник | себя |
| Характеристики | звезда, циклический, равносторонний, изогональный, изотоксальный |
| Звездные многоугольники |
|---|
В геометрия, октаграмма это восьмиугольный звездный многоугольник.
Название октаграмма объединить греческий цифровой префикс, окта, с Греческий суффикс -грамма. В -грамма суффикс происходит от γραμμή (граммḗ), что означает «линия».[1]
Деталь
 Правильная октаграмма с длиной каждой стороны, равной 1
Правильная октаграмма с длиной каждой стороны, равной 1
В общем, октаграмма - это любая самопересекающаяся восьмиугольник (8-сторонний многоугольник ).
В обычный октаграмма помечена Символ Шлефли {8/3}, что означает 8-сторонняя звезда, соединенная каждой третьей точкой.
Вариации
Эти варианты имеют нижний двугранный угол, Dih4, симметрия:
 Узкий  Широкий (Поворот на 45 градусов) |   Изотоксал |  Старый Флаг Чили содержала эту восьмиугольную звездную геометрию с удаленными краями ( Guñelve ). |  Геометрию можно настроить так, чтобы 3 кромки пересекались в одной точке, как Аусеклис символ |  8-балльная картушка можно рассматривать как восьмиугольную звезду с 4 главными точками и 4 второстепенными. |
Символ Руб эль-Хизб это Unicode глиф ۞ в U + 06DE.
Как квазиусеченный квадрат
Более глубокие усечения квадрата могут давать изогональные (вершинно-транзитивные) промежуточные формы звездообразного многоугольника с равным расстоянием между вершинами и двумя длинами ребер. Усеченный квадрат - это восьмиугольник, t {4} = {8}. Квазиусеченный квадрат, перевернутый как {4/3}, является октаграммой, t {4/3} = {8/3}.[2]
Униформа звездный многогранник звездчатый усеченный шестигранник, t '{4,3} = t {4 / 3,3} имеет грани октаграммы, построенные таким образом из куба. По этой причине его можно рассматривать как трехмерный аналог октаграммы.
| Обычный | Квазирегулярный | Изогональный | Квазирегулярный |
|---|---|---|---|
 {4} |  t {4} = {8} |  | 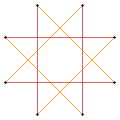 t '{4} = t {4/3} = {8/3} |
| Обычный | Униформа | Изогональный | Униформа |
 {4,3} |  т {4,3} |  |  т '{4,3} = т {4 / 3,3} |
Еще одна трехмерная версия октаграммы - это невыпуклый большой ромбокубооктаэдр (квазиромбокубооктаэдр), который можно представить как квазикантеллированный (квазирасширенный) куб, t0,2{4/3,3}.
Соединения звездообразных многоугольников
Есть две правильные восьмиугольные звездные фигуры (соединения) формы {8 / k}, первая построена как два квадрата {8/2} = 2 {4}, а вторая - как четыре вырожденных дигоны, {8/4} = 4 {2}. Существуют и другие изогональные и изотоксические соединения, включая прямоугольные и ромбические формы.
| Обычный | Изогональный | Изотоксал | ||
|---|---|---|---|---|
 а {8} = {8/2} = 2 {4} |  {8/4}=4{2} | 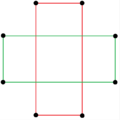 | 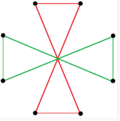 | 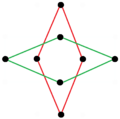 |
{8/2} или 2 {4}, например Диаграммы Кокстера ![]()
![]()
![]() +
+ ![]()
![]()
![]() , можно рассматривать как 2D-эквивалент 3D соединение куба и октаэдра,
, можно рассматривать как 2D-эквивалент 3D соединение куба и октаэдра, ![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() , 4D соединение тессеракта и 16 ячеек,
, 4D соединение тессеракта и 16 ячеек, ![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]()
![]()
![]() и 5D соединение 5-куба и 5-ортоплекса; то есть соединение n-куб и кросс-многогранник в их соответствующих двойных позициях.
и 5D соединение 5-куба и 5-ортоплекса; то есть соединение n-куб и кросс-многогранник в их соответствующих двойных позициях.
Другие представления восьмиугольной звезды
An восьмиугольная звезда можно рассматривать как вогнутую шестиугольник, с удалением внутренней пересекающейся геометрии. Также его можно рассечь радиальными линиями.
| 2{4} | 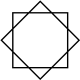 |  |  |  |
|---|---|---|---|---|
| {8/3} |  | 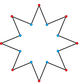 |  |  |
 |  |  |  | |
 |  |  |  |
Другое использование
- В Unicode, символ «восьмиконечной звездочки» ✳ - это U + 2733.
Смотрите также
- использование
- Руб эль-Хизб - Исламский характер
- Звезда Иштар - символ древней шумерской богини Инанна и ее восточно-семитский коллега Иштар и Роман Венера.
- Звезда Лакшми - индийский характер
- Сурья Маджапахит - использование во время Маджапахит раз в Индонезии, чтобы представить Индуистский боги направлений
- Картушка - использование в компасах для обозначения стороны света для восьми основные ветры
- Аусеклис - использование латышами регулярной октаграммы
- Guñelve - представление Венера в Мапуче иконография.
- Сельбуроз - использование регулярной октаграммы в норвежском дизайне
- Звезды вообще
Рекомендации
- ^ γραμμή, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ Светлая сторона математики: Материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум
- Грюнбаум, Б. и G.C. Шепард; Плитки и узоры, Нью-Йорк: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Грюнбаум, Б.; Многогранники с полыми гранями, Протокол конференции НАТО-АСИ по многогранникам ... и т. Д. (Торонто, 1993 г.), под ред. Т. Бистрички и др., Kluwer Academic (1994), стр. 43–70.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. с. 404: Правильные звездные многогранники размерности 2)

