Наклон многоугольника - Skew polygon

В геометрия, а наклонный многоугольник это многоугольник чьи вершины не все копланарный. У перекосных полигонов должно быть не менее четырех вершины. В интерьер поверхность (или площадь) такого многоугольника не определяется однозначно.
Наклонить бесконечные многоугольники (апейрогоны) имеют вершины, которые не все коллинеарны.
А зигзагообразный косой многоугольник или же антипризматический многоугольник[1] имеет вершины, которые чередуются на двух параллельных плоскостях и, следовательно, должны быть четными.
Правильные косые многоугольники в трех измерениях (и правильные косые апейрогоны в двух измерениях) всегда зигзагообразны.
Антипризматический косой многоугольник в трех измерениях

А правильный косой многоугольник является изогональный с равной длиной кромки. В трех измерениях правильный косой многоугольник - это зигзагообразный перекос (или же антипризматический многоугольник), вершины которого чередуются между двумя параллельными плоскостями. Боковые края п-антипризма можно определить регулярный перекос 2п-гон.
Правильному косому n-угольнику можно присвоить символ Шлефли {p} # {} как смешивать из правильный многоугольник {p} и ортогональный отрезок { }.[2] Операция симметрии между последовательными вершинами: скользящее отражение.
Примеры показаны на однородных квадратной и пятиугольной антипризмах. В звездные антипризмы также генерировать правильные косые многоугольники с разным порядком соединения верхнего и нижнего многоугольников. Закрашенные верхний и нижний многоугольники нарисованы для ясности структуры и не являются частью косых многоугольников.
| Косой квадрат | Наклоненный шестиугольник | Наклонный восьмиугольник | Наклон десятиугольника | Наклонный двенадцатигранник | ||
| {2}#{ } | {3}#{ } | {4}#{ } | {5}#{ } | {5/2}#{ } | {5/3}#{ } | {6}#{ } |
 | 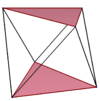 |  |  |  |  | 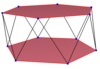 |
| с {2,4} | с {2,6} | с {2,8} | с {2,10} | ср {2,5 / 2} | с {2,10 / 3} | с {2,12} |
Обычный составной перекос 2п-gon можно построить аналогичным образом, добавив второй наклонный многоугольник путем поворота. Они имеют те же вершины, что и призматическое соединение антипризм.
| Косые квадраты | Скошенные шестиугольники | Наклон декагонов | |
| Два {2} # {} | Три {2} # {} | Два {3} # {} | Два {5/3} # {} |
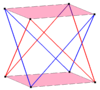 | 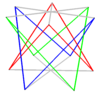 |  |  |
Полигоны Петри - правильные косые многоугольники, определенные внутри правильных многогранников и многогранников. Например, пять Платоновы тела имеют 4-, 6- и 10-сторонние правильные косые многоугольники, как показано на этих ортогональные проекции с красными краями вокруг соответствующих проекционные конверты. Тетраэдр и октаэдр включают все вершины в их соответствующих зигзагообразных скошенных многоугольниках и могут рассматриваться как двуугольная антипризма и треугольная антипризма соответственно.

Правильный косой многоугольник как вершинная фигура правильного косого многогранника
А правильный косой многогранник имеет правильные многоугольные грани и правильный косой многоугольник вершина фигуры.
Три бесконечных правильных косых многогранника - это заполнение пространства в 3-м пространстве; другие существовать в 4-м пространстве, некоторые в равномерные 4-многогранники.
| {4,6|4} | {6,4|4} | {6,6|3} |
|---|---|---|
 Правильный косой шестиугольник {3}#{ } |  Обычный перекос {2}#{ } | 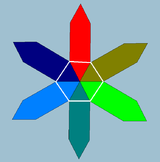 Правильный косой шестиугольник {3}#{ } |
Изогональные косые многоугольники в трех измерениях
An изогональный наклонный многоугольник представляет собой косой многоугольник с одним типом вершины, соединенный двумя типами ребер. Изогональные косые многоугольники с равной длиной ребер также можно считать квазирегулярными. Он похож на зигзагообразный многоугольник с перекосом, существующий в двух плоскостях, за исключением того, что позволяет одному краю пересекать противоположную плоскость, а другому краю оставаться в той же плоскости.
Изогональные косые многоугольники могут быть определены на четных n-угольных призмах, попеременно следующих за краем одного бокового многоугольника и перемещаясь между многоугольниками. Например, по вершинам куба. Вершины чередуются между верхним и нижним квадратами с красными краями между сторонами и синими краями вдоль каждой стороны.
| Восьмиугольник | Додекагон | Икосикаитетрагон | ||||
|---|---|---|---|---|---|---|
 Куб, квадратно-диагональный |  Куб |  Перекрещенный куб | 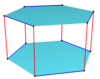 Гексагональная призма | 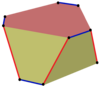 Гексагональная призма | 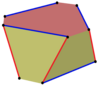 Гексагональная призма |  Витая призма |
Правильные наклонные многоугольники в четырех измерениях
В четырех измерениях правильный косой многоугольник может иметь вершины на Клиффорд тор и связаны Смещение Клиффорда. В отличие от зигзагообразных косых многоугольников, косые многоугольники при двойном повороте могут иметь нечетное количество сторон.
В Полигоны Петри из правильные 4-многогранники определить правильные косые многоугольники. В Число Кокстера для каждого группа Кокстера Симметрия выражает, сколько сторон имеет многоугольник Петри. Это 5 сторон для 5-элементный, 8 сторон для тессеракт и 16 ячеек, 12 сторон для 24-элементный, и 30 сторон для 120 ячеек и 600 ячеек.
При ортогональном проецировании на Самолет Кокстера, эти правильные наклонные многоугольники выглядят на плоскости как правильные огибающие многоугольников.
| А4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | ЧАС4, [5,3,3] | ||
|---|---|---|---|---|---|
| Пентагон | Восьмиугольник | Додекагон | Триаконтагон | ||
 5-элементный {3,3,3} |  тессеракт {4,3,3} |  16 ячеек {3,3,4} |  24-элементный {3,4,3} |  120 ячеек {5,3,3} |  600 ячеек {3,3,5} |
В п-п дуопризма и двойной дуопирамиды также есть 2п-гональные многоугольники Петри. (The тессеракт это 4-4 дуопризма, а 16 ячеек представляет собой 4-4 дуопирамиду.)
| Шестиугольник | Декагон | Додекагон | |||
|---|---|---|---|---|---|
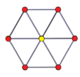 3-3 дуопризма |  3-3 дуопирамида | 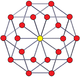 5-5 дуопризма | 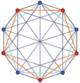 5-5 дуопирамид |  6-6 дуопризма |  6-6 дуопирамид |
Смотрите также
- Многоугольник Петри
- Четырехугольник # Косые четырехугольники
- Правильный косой многогранник
- Косой апейроэдр (бесконечный косой многогранник)
- Наклонные линии
Рекомендации
- Макмаллен, Питер; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Издательство Кембриджского университета, ISBN 0-521-81496-0 п. 25
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. "Косые многоугольники (седловидные многоугольники)" §2.2
- Coxeter, H.S.M .; Правильные сложные многогранники (1974). Глава 1. Правильные многоугольники, 1.5. Правильные многоугольники в n измерениях, 1.7. Зигзагообразные и антипризматические многоугольники, 1.8. Спиральные многоугольники. 4.3. Флаги и орто-схемы, 11.3. Полигоны Петри
- Coxeter, Х.С.М. Полигоны Петри. Правильные многогранники, 3-е изд. Нью-Йорк: Дувр, 1973 г. (раздел 2.6 Полигоны Петри стр. 24–25 и Глава 12, стр. 213–235, Обобщенный многоугольник Петри)
- Кокстер, Х. С. М. и Мозер, В. О. Дж. (1980). Генераторы и соотношения для дискретных групп. Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9. (1-е изд, 1957 г.) 5.2. Многоугольник Петри {p, q}.
- Джон Милнор: О полной кривизне узлов, Анна. Математика. 52 (1950) 248–257.
- Дж. М. Салливан: Кривые конечной полной кривизны, ArXiv: math.0606007v2
