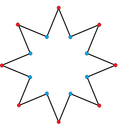
Шестиугольник - Hexadecagon

Правильный шестиугольник
Правильный шестиугольник
Тип	Правильный многоугольник
Края и вершины	16
Символ Шлефли	{16}, т {8}, тт {4}
Диаграмма Кокстера
Группа симметрии	Двугранный (D16), порядок 2 × 16
Внутренний угол (градусы )	157.5°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В математике шестиугольник (иногда называемый шестиугольник или же 16-угольник) является шестнадцатигранным многоугольник.^[1]

Правильный шестиугольник

А обычный шестиугольник представляет собой шестиугольник, в котором все углы равны и все стороны равны. Его Символ Шлефли есть {16} и может быть построен как усеченный восьмиугольник, t {8}, и дважды усеченный квадрат tt {4}. Усеченный шестиугольник, t {16}, является триаконтадигон, {32}.

Строительство

Поскольку 16 = 2⁴ (а сила двух ) правильный шестиугольник конструктивный с помощью компас и линейка: это было уже известно древнегреческим математикам.^[2]

Построение правильного шестиугольника
в данном описанном круге

Построение правильного шестиугольника
при заданной длине стороны, анимация. (Конструкция очень похожа на восьмиугольник с заданной длиной стороны.)

Измерения

Каждый угол правильного шестиугольника равен 157,5. градусы, а общий угол любого шестиугольника составляет 2520 градусов.

В площадь правильного шестиугольника с длиной ребра т является

${displaystyle {egin{aligned}A=4t^{2}cot {frac {pi }{16}}=&4t^{2}left(1+{sqrt {2}}+{sqrt {4+2{sqrt {2}}}}ight)=&4t^{2}({sqrt {2}}+1)({sqrt {4-2{sqrt {2}}}}+1).end{aligned}}}$

Поскольку у шестиугольника есть несколько сторон, сила двух, его площадь может быть вычислена через по окружности р путем усечения Формула Вьете:

${displaystyle A=R^{2}cdot {frac {2}{1}}cdot {frac {2}{sqrt {2}}}cdot {frac {2}{sqrt {2+{sqrt {2}}}}}=4R^{2}{sqrt {2-{sqrt {2}}}}.}$

Поскольку площадь описанной окружности равна ${displaystyle pi R^{2},}$ правильный шестиугольник заполняет примерно 97,45% описанной окружности.

Симметрия

Симметрия

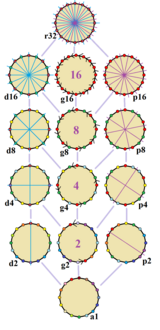14 симметрий правильного шестиугольника. Линии отражений синие по вершинам, пурпурные по краям, а порядок вращения указан в центре. Вершины окрашены в соответствии с их положением симметрии.

В правильный шестиугольник есть Dih₁₆ симметрия, порядок 32. Есть 4 диэдральные подгруппы: Dih₈, Ди₄, Ди₂, и Dih₁, и 5 циклические подгруппы: Z₁₆, Z₈, Z₄, Z₂, а Z₁, последнее подразумевает отсутствие симметрии.

На правильном шестиугольнике имеется 14 различных симметрий. Джон Конвей называет полную симметрию r32 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров) Циклические симметрии в среднем столбце помечены как грамм для их приказов центрального вращения.^[3]

Наиболее распространенными шестиугольниками высокой симметрии являются: d16, изогональный шестиугольник, состоящий из восьми зеркал, может чередовать длинные и короткие края, и p16, изотоксальный шестиугольник, состоящий из ребер равной длины, но чередующиеся вершинами под двумя разными внутренними углами. Эти две формы двойники друг друга и имеют половину порядка симметрии правильного шестиугольника.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g16 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

16-куб проекция	112 рассечение ромба
	Обычный	Изотоксал

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[4]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Для правильный шестиугольник, м= 8, и его можно разделить на 28: 4 квадрата и 3 набора по 8 ромбов. Это разложение основано на Многоугольник Петри проекция 8-куб, с 28 из 1792 лиц. Список OEIS: A006245 Перечисляет количество решений как 1232944, включая до 16-кратного поворота и хиральные формы в отражении.

Рассечение на 28 ромбов

8-куб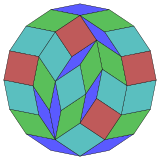

Перекос шестиугольника

3 правильных косых зигзагообразных шестиугольника

{8}#{ }	{​^8⁄3}#{ }	{​^8⁄5}#{ }
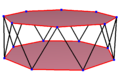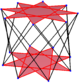Правильный наклонный шестиугольник выглядит как зигзагообразные края восьмиугольная антипризма, октаграмматическая антипризма, и октаграммная скрещенная антипризма.

А перекос шестиугольника это наклонный многоугольник с 24 вершинами и ребрами, но не в одной плоскости. Внутренность такого шестиугольника обычно не определяется. А перекос зигзагообразный шестиугольник имеет чередующиеся вершины между двумя параллельными плоскостями.

А правильный скошенный шестиугольник является вершинно-транзитивный с равной длиной кромки. В 3-х измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых краях восьмиугольная антипризма с тем же D_8d, [2⁺, 16] симметрия порядка 32. октаграмматическая антипризма, s {2,16 / 3} и октаграммная скрещенная антипризма, s {2,16 / 5} также имеют правильные скошенные восьмиугольники.

Полигоны Петри

Правильный шестиугольник - это Многоугольник Петри для многих многомерных многогранников, показанных на этих наклонных ортогональные проекции, включая:

А15	B8		D9		2B2 (4D)
15-симплекс	8-ортоплекс	8-куб	611	161	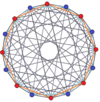8-8 дуопирамид	8-8 дуопризма

Связанные цифры

А гексадекаграмма представляет собой звездообразный многоугольник с 16 сторонами, представленный символом {16 / n}. Есть три обычных звездные многоугольники, {16/3}, {16/5}, {16/7}, используя те же вершины, но соединяя каждую третью, пятую или седьмую точки. Также есть три соединения: {16/2} сокращается до 2 {8} как два восьмиугольники, {16/4} уменьшается до 4 {4} как четыре квадрата, а {16/6} уменьшается до 2 {8/3} как два октаграммы, и, наконец, {16/8} уменьшается до 8 {2} как восемь дигоны.

Составные и звездные шестиугольники
Форма	Выпуклый многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{16/1} или {16}	{16/2} или 2 {8}	{16/3}	{16/4} или 4 {4}
Внутренний угол	157.5°	135°	112.5°	90°
Форма	Звездный многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{16/5}	{16/6} или 2 {8/3}	{16/7}	{16/8} или 8 {2}
Внутренний угол	67.5°	45°	22.5°	0°

Более глубокие усечения правильного восьмиугольника и октаграммы могут давать изогональные (вершинно-транзитивный ) промежуточные гексадекаграммы образуются с одинаковыми вершинами и двумя длинами ребер.^[5]

Усеченный восьмиугольник - это шестиугольник, t {8} = {16}. Квазиусеченный восьмиугольник, перевернутый как {8/7}, представляет собой гексадикаграмму: t {8/7} = {16/7}. Усеченная октаграмма {8/3} представляет собой гексадекаграмму: t {8/3} = {16/3}, а квазиусеченная октаграмма, перевернутая как {8/5}, является гексадекаграммой: t {8/5} = {16 / 5}.

Изогональные усечения восьмиугольника и октаграммы
Квазирегулярный	Изогональный			Квазирегулярный
t {8} = {16}				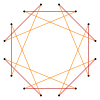т {8/7} = {16/7}
т {8/3} = {16/3}		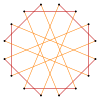		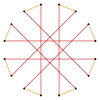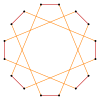т {8/5} = {16/5}

В искусстве

Шестиугольная башня из Рафаэля Женитьба Богородицы

В начале 16 века Рафаэль был первым, кто построил перспектива изображение правильного шестиугольника: башня на его картине Женитьба Богородицы имеет 16 сторон, развивая восьмиугольную башню на предыдущей картине автора Пьетро Перуджино.^[6]

Шестнадцатеричный узор из Альгамбра

Гексадекаграммы (16-сторонние звездные многоугольники ) включены в Гирих шаблоны в Альгамбра.^[7]

Другие

в Филиппины, на местных карнавалах (периахан), колеса обозрения на 16 мест или гондолы.

В Мехико 'Parque del ejecutivo' - это небольшой шестиугольный парк, окруженный шестиугольной кольцевой дорогой, а также 16 дорогами, которые проходят радиально наружу, создавая в процессе более крупные шестиугольники. Просмотр карт Google

Неправильные шестиугольники

An восьмиугольная звезда можно рассматривать как вогнутый шестиугольник:

Смотрите также

• Сеть Rhumbline

Рекомендации

1. Вайсштейн, Эрик В. (2002). CRC Краткая энциклопедия математики, второе издание. CRC Press. п. 1365. ISBN  9781420035223.
2. Коши, Томас (2007), Элементарная теория чисел с приложениями (2-е изд.), Academic Press, стр. 142, ISBN  9780080547091.
3. Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN  978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
4. Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
5. Более светлая сторона математики: материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум
6. Шпейзер, Дэвид (2011), «Архитектура, математика и теология в картинах Рафаэля», в Уильямс, Ким (ред.), Перекресток: история науки, история искусства. Очерки Дэвида Спейзера, т. II, Springer, стр. 29–39, Дои:10.1007/978-3-0348-0139-3_3. Первоначально опубликовано в Nexus III: архитектура и математика, Ким Уильямс, изд. (Оспедалетто, Пиза: Pacini Editore, 2000), стр. 147–156.
7. Ханкин, Э. Ханбери (май 1925 г.), «Примеры методов рисования геометрических арабесков», Математический вестник, 12 (176): 370–373, Дои:10.2307/3604213.

внешняя ссылка

• Вайсштейн, Эрик В. «Шестиугольник». MathWorld.