Восьмиугольник - Octadecagon

Правильный восьмиугольник
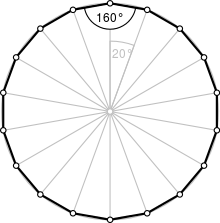Правильный восьмиугольник
Тип	Правильный многоугольник
Края и вершины	18
Символ Шлефли	{18}, т {9}
Диаграмма Кокстера
Группа симметрии	Двугранный (D18), заказ 2 × 18
Внутренний угол (градусы )	160°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, восьмиугольник (или же восьмиугольник^[1]) или 18-угольник - это восемнадцатигранный многоугольник.^[2]

Правильный восьмиугольник

Восьмиугольник со всеми 135 диагоналями

А обычный восьмиугольник имеет Символ Шлефли {18} и может быть построен как квазирегулярный усеченный девятиугольник, t {9}, который чередует два типа ребер.

строительство

Поскольку 18 = 2 × 3², правильный восьмиугольник не может быть построен с помощью компас и линейка.^[3] Однако его можно построить, используя Neusis, или трисекция угла с томагавк.

Октадекагон, точная конструкция на основе трисекции угла 120 ° с помощью томагавка, анимация 1 мин. 34 с.

Следующая приблизительная конструкция очень похожа на конструкцию эннеагона, поскольку восьмиугольник можно построить как усеченный эннеагон. Это также возможно с исключительным использованием компаса и линейки.

Уменьшите угол AMC (также 60 °) с четырьмя биссектрисами и сделайте 1/3 дуги окружности MON с приближенным решением между биссектрисами углов w3 и ж4. Прямая вспомогательная линия g направлена ​​через точку O в точку N (фактически это линейка в точках O и N), между O и N, поэтому вспомогательной линии нет. Таким образом, дуга окружности MON доступна для более поздней точки пересечения R. ${\displaystyle \scriptstyle \angle {}}$ AMR = 19,999999994755615 ... ° 360° ÷ 18 = 20° ${\displaystyle \scriptstyle \angle {}}$ AMR - 20 ° = -5,244 ... E-9 ° Пример для иллюстрации ошибки: При радиусе описанной окружности r = 100000 км абсолютная погрешность 1-й стороны будет примерно -9 мм. См. Также расчет наноган (Berechnung, нем.) 6.0 ${\displaystyle \scriptstyle \angle {}}$ Эквивалент JMR ${\displaystyle \scriptstyle \angle {}}$ AMR.

Симметрия

Симметрии правильного восьмиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркала прорисовываются через вершины, а фиолетовые зеркала - через края. В центре даны приказы гирации.

В правильный восьмиугольник имеет Dih₁₈ симметрия, порядок 36. Существует 5 диэдральных симметрий подгрупп: Dih₉, (Dih₆, Ди₃) и (Dih₂ Dih₁) и 6 циклическая группа симметрии: (Z₁₈, Z₉), (Z₆, Z₃) и (Z₂, Z₁).

Эти 15 симметрий можно увидеть в 12 различных симметриях восьмиугольника. Джон Конвей помечает их буквой и групповым порядком.^[4] Полная симметрия правильной формы r36 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров), и я когда линии отражения проходят через ребра и вершины. Циклические симметрии в среднем столбце помечены как грамм для их приказов центрального вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g18 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

18-угольник со 144 ромбами

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[5]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильный восьмиугольник, м= 9, и его можно разделить на 36: 4 набора по 9 ромбов. Это разложение основано на Многоугольник Петри проекция 9-куб, с 36 из 4608 лиц. Список OEIS: A006245 Перечисляет количество решений как 112018190, включая до 18-кратных поворотов и хиральных форм в отражении.

Рассечение на 36 ромбов

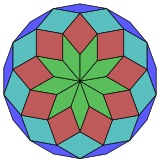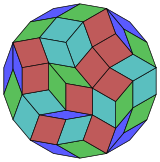Использует

Правильный треугольник, девятиугольник и восьмиугольник могут полностью окружать точку на плоскости, это одна из 17 различных комбинаций правильных многоугольников с этим свойством.^[6] Однако этот шаблон нельзя распространить на Архимедова черепица плоскости: поскольку у треугольника и девятиугольника нечетное количество сторон, ни одна из них не может быть полностью окружена кольцом, чередующим два других типа многоугольников.

Правильный восьмиугольник может разбить плоскость мозаикой с вогнутыми шестиугольными промежутками. И еще один тайлинг смешивается с неагонами и восьмиугольными промежутками. Первый тайлинг связан с усеченная шестиугольная мозаика, а второй усеченная трехгексагональная мозаика.

Связанные цифры

An октадекаграмма представляет собой 18-сторонний звездообразный многоугольник, представленный символом {18 / n}. Есть два обычных звездные многоугольники: {18/5} и {18/7}, используя одни и те же точки, но соединяя каждую пятую или седьмую точки. Также есть пять соединений: {18/2} сокращается до 2 {9} или двух эннеагоны, {18/3} сокращается до 3 {6} или трех шестиугольники, {18/4} и {18/8} сокращаются до 2 {9/2} и 2 {9/4} или двух эннеаграммы, {18/6} сокращается до 6 {3} или 6 равносторонних треугольников, и, наконец, {18/9} сокращается до 9 {2} как девять дигоны.

Соединения и звездообразные многоугольники
п	1	2	3	4	5	6	7	8	9
Форма	Выпуклый многоугольник	Соединения			Звездный многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{18/1} = {18}	{18/2} = 2{9}	{18/3} = 3{6}	{18/4} = 2{9/2}	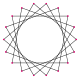{18/5}	{18/6} = 6{3}	{18/7}	{18/8} = 2{9/4}	{18/9} = 9{2}
Внутренний угол	160°	140°	120°	100°	80°	60°	40°	20°	0°

Более глубокие усечения регулярной эннеаграммы и эннеаграммы могут давать изогональные (вершинно-транзитивный ) промежуточные формы октадекаграммы с одинаково расположенными вершинами и двумя длинами ребер. Другие усечения образуют двойные покрытия: t {9/8} = {18/8} = 2 {9/4}, t {9/4} = {18/4} = 2 {9/2}, t {9 / 2} = {18/2} = 2 {9}.^[7]

Вершинно-транзитивные усечения эннеаграмм и эннеаграмм
Квазирегулярный	изогональный				Квазирегулярный Двойное покрытие
t {9} = {18}				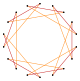	т {9/8} = {18/8} =2{9/4}
т {9/5} = {18/5}					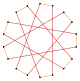т {9/4} = {18/4} =2{9/2}
т {9/7} = {18/7}		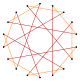			т {9/2} = {18/2} =2{9}

Полигоны Петри

Правильный восьмиугольник - это Многоугольник Петри для ряда многомерных многогранников, показанных на этих наклонных ортогональные проекции из Самолеты Кокстера:

Восьмиугольные многоугольники петри
А17	B9		D10		E7
17-симплекс	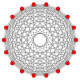9-ортоплекс	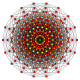9-куб	711	171	321	231	132

Рекомендации

1. Кинси, Л. Кристин; Мур, Тереза ​​Э. (2002), Симметрия, форма и поверхности: введение в математику через геометрию, Springer, стр. 86, ISBN  9781930190092.
2. Адамс, Генри (1907), Справочник инженера Касселла: факты и формулы, принципы и практика во всех отраслях техники, Д. Маккей, стр. 528.
3. Конвей, Джон Б. (2010), Математические связи: основной курс, Американское математическое общество, стр. 31, ISBN  9780821849798.
4. Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN  978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
5. Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
6. Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. Д., Джон У. Паркер и сын, стр. 134.
7. Более светлая сторона математики: материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум

• восьмиугольник

внешняя ссылка

• Вайсштейн, Эрик В. «Восьмиугольник». MathWorld.