Греки (финансы) - Greeks (finance)

В математические финансы, то Греки являются количествами, представляющими чувствительность цены производные Такие как опции к изменению основных параметры на котором стоимость инструмента или портфолио из финансовые инструменты зависим. Это название используется потому, что наиболее распространенные из этих чувствительности обозначены Греческие буквы (как и некоторые другие финансовые меры). В совокупности их также называют чувствительность к риску,^[1] меры риска^[2]:742 или же параметры хеджирования.^[3]

Использование греков

Место Цены) Волатильность (${\displaystyle \sigma }$) Время истечение срока (${\displaystyle \tau }$) Значение (V) ${\displaystyle \Delta }$ Дельта ${\displaystyle {\mathcal {V}}}$ Вега ${\displaystyle \Theta }$ Тета Дельта (${\displaystyle \Delta }$)  ${\displaystyle \Gamma }$ Гамма Vanna Очарование Вега (${\displaystyle {\mathcal {V}}}$)  Vanna Вомма Вета Тета (${\displaystyle \Theta }$)  Очарование Вета Гамма (${\displaystyle \Gamma }$)  Скорость Зомма Цвет Вомма Ultima

Определение греков как чувствительность цены и риска опциона (в первой строке) к базовому параметру (в первом столбце). Греки первого порядка выделены синим цветом, греки второго порядка - зеленым, а греки третьего порядка - желтым. Обратите внимание, что vanna, charm и veta появляются дважды, поскольку частные кросс-производные равны Теорема Шварца. Rho, lambda, epsilon и vera опущены, поскольку они не так важны, как остальные. Три места в таблице не заняты, поскольку соответствующие количества еще не определены в финансовой литературе.

Греки - жизненно важные инструменты в управление рисками. Каждый грек измеряет чувствительность стоимости портфеля до небольшого изменения данного базового параметра, так что риски компонентов могут рассматриваться изолированно, а портфель соответственно перебалансирован для достижения желаемой подверженности риску; см. например дельта-хеджирование.

Греки в Модель Блэка – Шоулза относительно легко вычислить, желаемое свойство финансовый модели, и очень полезны для трейдеров деривативов, особенно тех, кто стремится застраховать свои портфели от неблагоприятных изменений рыночных условий. По этой причине те греки, которые особенно полезны для хеджирования, такие как дельта, тета и вегета, хорошо определены для измерения изменений цены, времени и волатильности. Хотя rho является основным входом в модель Блэка – Шоулза, общее влияние на стоимость варианта, соответствующее изменениям в безрисковая процентная ставка обычно незначительна, и поэтому производные финансовые инструменты более высокого порядка, включающие безрисковую процентную ставку, не являются обычным явлением.

Наиболее распространены у греков производные первого порядка: дельта, Вега, тета и ро а также гамма, производная второго порядка функции цены. Остальные уязвимости в этом списке достаточно распространены, чтобы иметь общие названия, но этот список ни в коем случае не является исчерпывающим.

Имена

Использование греческих буквенных названий предположительно является продолжением общих финансовых терминов. альфа и бета, и использование сигма (стандартное отклонение логарифмической доходности) и тау (время до истечения срока) в Модель ценообразования опционов Блэка – Шоулза. Придумано несколько имен, таких как «вега» и «зомма», но по звучанию они похожи на греческие буквы. Названия «цвет» и «очарование», вероятно, происходят от использования этих терминов для обозначения экзотических свойств кварки в физика элементарных частиц.

Греки первого порядка

Дельта

Дельта,^[4] ${\displaystyle \Delta }$, измеряет скорость изменения теоретической стоимости опциона по отношению к изменениям цены базового актива. Дельта - это первая производная ценности ${\displaystyle V}$ опциона на цену базового инструмента ${\displaystyle S}$.

${\displaystyle \Delta ={\frac {\partial V}{\partial S}}}$

Практическое использование

Для ванильного варианта дельта будет числом от 0,0 до 1,0 для длинного вызов (или короткий пут) и 0,0 и -1,0 для длинных положить (или короткий звонок); в зависимости от цены опцион колл ведет себя так, как если бы кто-то владеет 100 акциями базовой акции (если в деньгах), или ничего не владеет (если далеко не в деньгах), или что-то среднее, и, наоборот, для опциона пут. Разница между дельтой колла и дельтой пут при одном и том же страйке равна единице. К паритет пут – колл, длинный колл и короткий пут эквивалентны форвардному F, линейная в пятне S, с единичным коэффициентом, поэтому производная dF / dS равна 1. См. формулы ниже.

Эти числа обычно представлены как процент от общего количества акций, представленных опционными контрактами. Это удобно, потому что опцион (мгновенно) будет вести себя как количество акций, указанное дельтой. Например, если портфель из 100 американских колл-опционов на XYZ каждый имеет дельту 0,25 (= 25%), он будет расти или терять стоимость, как 2500 акций XYZ, когда цена изменяется при небольших колебаниях цены (100 опционных контрактов покрывают 10 000 акций). Знак и процент часто опускаются - знак подразумевается в типе опциона (отрицательный для пут, положительный для колл), и процент понимается. Наиболее часто котируются 25 дельта пут, 50 дельта пут / 50 дельта колл и 25 дельта колл. 50 Delta put и 50 Delta call не совсем идентичны из-за того, что спот и форвард различаются коэффициентом дисконтирования, но они часто объединяются.

Дельта всегда положительна для длинных коллов и отрицательна для длинных путов (если они не равны нулю). Общую дельту сложного портфеля позиций по одному и тому же базовому активу можно рассчитать, просто взяв сумму дельт для каждой отдельной позиции - дельта портфеля линейна по составляющим. Поскольку дельта базового актива всегда равна 1,0, трейдер может дельта-хеджирование вся его позиция в базовом активе путем покупки или короткой продажи количества акций, обозначенного общей дельтой. Например, если дельта портфеля опционов в XYZ (выраженная в долях базового актива) равна +2,75, трейдер сможет дельта-хеджировать портфель путем короткие продажи 2,75 акции базового актива. Тогда этот портфель сохранит свою общую стоимость независимо от того, в каком направлении движется цена XYZ. (Хотя только для небольших движений базового актива, короткого промежутка времени и невзирая на изменения в других рыночных условиях, таких как волатильность и норма доходности для безрисковых инвестиций).

Как показатель вероятности

Основная статья: Денежность

(Абсолютное значение) Дельта близко, но не идентично проценту денежность варианта, т.е. подразумевается вероятность истечения срока опциона в деньгах (если рынок опускается ниже Броуновское движение в нейтральная к риску мера ).^[5] По этой причине некоторые опционные трейдеры используют абсолютное значение дельты в качестве приближения к процентной денежности. Например, если вне денег У опциона колл дельта 0,15, трейдер может оценить, что вероятность истечения опциона при деньгах составляет примерно 15%. Точно так же, если дельта контракта пут составляет -0,25, трейдер может ожидать, что опцион будет иметь 25% вероятность истечения при деньгах. При деньгах коллы и путы имеют дельту приблизительно 0,5 и -0,5 соответственно с небольшим уклоном в сторону более высоких дельт для вызовов ATM. Фактическая вероятность того, что опцион закончится в деньгах, - это его двойная дельта, которая является первой производной от цены опциона по страйку.^[6]

Связь между дельтой колл и пут

Учитывая европейский опцион колл и пут для одного и того же базового актива, цену исполнения и время до погашения, а также без дивидендной доходности, сумма абсолютных значений дельты каждого опциона будет равна 1 - точнее, дельте колла ( положительное) минус дельта пут (отрицательное) равно 1. Это связано с паритет пут – колл: длинный колл плюс короткий пут (колл минус пут) воспроизводит форвард, дельта которого равна 1.

Если значение дельты для опциона известно, можно рассчитать значение дельты опциона с той же страйк-ценой, базовым активом и сроком погашения, но напротив справа, вычитая 1 из известной дельты колл или прибавляя 1 к известной дельте пут. .

${\displaystyle \Delta (call)-\Delta (put)=1}$, следовательно: ${\displaystyle \Delta (call)=\Delta (put)+1}$ и ${\displaystyle \Delta (put)=\Delta (call)-1}$.

Например, если дельта колла равна 0,42, то можно вычислить дельту соответствующего опциона пут при той же цене страйка на 0,42 - 1 = -0,58. Чтобы получить дельту колла из пут, аналогичным образом можно взять -0,58 и прибавить 1, чтобы получить 0,42.

Вега

Вега^[4] измеряет чувствительность к непостоянство. Vega - это производная от стоимости опциона по отношению к непостоянство базового актива.

${\displaystyle {\mathcal {V}}={\frac {\partial V}{\partial \sigma }}}$

Вега это не название какой-либо греческой буквы. Используемый глиф представляет собой нестандартную маюскульную версию греческой буквы. ню, ${\displaystyle \nu }$, записанный как ${\displaystyle {\mathcal {V}}}$. Предположительно имя Вега был принят, потому что греческая буква ню выглядел как латынь Ви, и Вега был получен из Ви по аналогии с как бета, эта, и тета произносятся в американском английском.

Символ каппа, ${\displaystyle \kappa }$, иногда используется (учеными) вместо Вега (как есть тау (${\displaystyle \tau }$) или заглавная лямбда (${\displaystyle \Lambda }$),^[7]:315хотя такие редкие).

Вега обычно выражается как сумма денег на базовую акцию, которую стоимость опциона будет увеличивать или терять при повышении или понижении волатильности на 1. процентный пункт. Все опционы (как коллы, так и путы) будут иметь ценность с ростом волатильности.

Вега может быть важным греческим индикатором, за которым следует следить для трейдера опционов, особенно на волатильных рынках, поскольку стоимость некоторых опционных стратегий может быть особенно чувствительной к изменениям волатильности. Ценность "при деньгах" вариант стрэддл, например, очень сильно зависит от изменений волатильности.

Тета

Тета,^[4] ${\displaystyle \Theta }$, измеряет чувствительность значения производной к течению времени (см. Временная стоимость опциона ): «время распада».

${\displaystyle \Theta =-{\frac {\partial V}{\partial \tau }}}$

Математический результат формулы для теты (см. Ниже) выражается в годовой стоимости. По соглашению, результат обычно делится на количество дней в году, чтобы получить величину, на которую упадет цена опциона по отношению к цене базовой акции. Тэта почти всегда отрицательна для длинных коллов и путов и положительна для коротких (или письменных) коллов и путов. Исключение составляет европейский пут с большой прибылью. Общая тэта для портфеля опционов может быть определена путем суммирования тэта для каждой отдельной позиции.

Стоимость опциона можно разделить на две части: внутренняя стоимость и временная стоимость. Внутренняя стоимость - это сумма денег, которую вы получили бы, если бы вы исполнили опцион немедленно, поэтому колл со страйком 50 долларов по акции с ценой 60 долларов будет иметь внутреннюю стоимость 10 долларов, тогда как соответствующий пут будет иметь нулевую внутреннюю стоимость. Ценность времени - это ценность возможности подождать дольше, прежде чем принять решение о тренировке. Даже глубоко из денег пут будет чего-то стоить, так как есть некоторая вероятность того, что цена акции упадет ниже страйка до истечения срока действия. Однако по мере приближения срока погашения вероятность того, что это произойдет, уменьшается, поэтому временная стоимость опциона со временем уменьшается. Таким образом, если у вас длинная позиция по опциону, у вас короткая тета: ваш портфель будет терять ценность с течением времени (все остальные факторы остаются неизменными).

Ро

Ро,^[4] ${\displaystyle \rho }$, измеряет чувствительность к процентной ставке: это производная от стоимости опциона по безрисковой процентной ставке (для соответствующего непогашенного срока).

${\displaystyle \rho ={\frac {\partial V}{\partial r}}}$

За исключением чрезвычайных обстоятельств, стоимость опциона менее чувствительна к изменениям безрисковой процентной ставки, чем к изменениям других параметров. По этой причине ро является наименее используемым из греков первого порядка.

Rho обычно выражается как сумма денег на акцию базового актива, которую стоимость опциона будет увеличивать или терять при повышении или понижении безрисковой процентной ставки на 1,0% в год (100 базисных пунктов).

Лямбда

Лямбда,^[4] ${\displaystyle \lambda }$, омега,^[8] ${\displaystyle \Omega }$, или же эластичность^[4] это процент изменение стоимости опциона на процентное изменение базовой цены, мера использовать, иногда называемый передачей.

${\displaystyle \lambda =\Omega ={\frac {\partial V}{\partial S}}\times {\frac {S}{V}}}$

Он считает, что ${\displaystyle \lambda =\Omega =\Delta \times {\frac {S}{V}}}$.

Эпсилон

Эпсилон,^[9] ${\displaystyle \epsilon }$ (также известный как psi, ${\displaystyle \psi }$), - процентное изменение стоимости опциона на процент изменение основного дивиденд доходность, мера дивидендного риска. Влияние на дивидендную доходность на практике определяется с использованием 10% увеличения этой доходности. Очевидно, что эта чувствительность может применяться только к производным инструментам беспристрастность товары.

${\displaystyle \epsilon =\psi ={\frac {\partial V}{\partial q}}}$

Греки второго порядка

Гамма

Гамма,^[4] ${\displaystyle \Gamma }$, измеряет скорость изменения дельты относительно изменений базовой цены. Гамма вторая производная функции стоимости по отношению к базовой цене.

${\displaystyle \Gamma ={\frac {\partial \Delta }{\partial S}}={\frac {\partial ^{2}V}{\partial S^{2}}}}$

Большинство длинных вариантов имеют положительную гамму, а самые короткие варианты - отрицательную. Длинные опционы имеют положительную связь с гаммой, потому что по мере роста цены гамма также увеличивается, в результате чего дельта приближается к 1 из 0 (длинный опцион колл) и 0 из -1 (длинный опцион пут). Обратное верно для коротких опционов.^[10]

Дельта длинного опциона, цена базового актива и гамма.^[11]

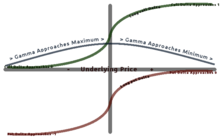
Гамма максимальна приблизительно при деньгах (банкомат) и уменьшается по мере того, как вы уходите в деньгах (ITM) или вне денег (OTM). Гамма важна, потому что она корректирует выпуклость ценности.

Когда трейдер пытается установить эффективное дельта-хеджирование для портфеля, трейдер может также попытаться нейтрализовать гамму портфеля, поскольку это гарантирует, что хеджирование будет эффективным в более широком диапазоне движений базовой цены.

Vanna

Vanna,^[4] также упоминается как ДвегаДспот^[12] и DdeltaDvol,^[12] является производной второго порядка от стоимости опциона один раз до базового спотовая цена и один раз к волатильности. Это математически эквивалентно DdeltaDvol, чувствительность дельты опциона к изменению волатильности; или, в качестве альтернативы, часть vega относительно цены базового инструмента. Vanna может быть полезной чувствительностью для мониторинга при поддержании портфеля с дельта- или вегетативным хеджированием, поскольку vanna поможет трейдеру предвидеть изменения в эффективности дельта-хеджирования по мере изменения волатильности или эффективности вегета-хеджирования против изменения базовая спотовая цена.

Если базовая стоимость имеет непрерывные вторые частные производные, то ${\displaystyle {\text{Vanna}}={\frac {\partial \Delta }{\partial \sigma }}={\frac {\partial {\mathcal {V}}}{\partial S}}={\frac {\partial ^{2}V}{\partial S\partial \sigma }}}$,

Очарование

Очарование^[4] или же дельта-распад^[13] измеряет мгновенную скорость изменения дельты с течением времени.

${\displaystyle {\text{Charm}}=-{\frac {\partial \Delta }{\partial \tau }}={\frac {\partial \Theta }{\partial S}}=-{\frac {\partial ^{2}V}{\partial \tau \,\partial S}}}$

Очарование также называли DdeltaDtime.^[12] Очарование может быть важным греческим фактором для измерения / мониторинга при дельта-хеджировании позиции на выходных. Очарование - это производная второго порядка от стоимости опциона: один раз - цена, а второй - время. Это также производная от тета относительно цены базового актива.

Математический результат формулы очарования (см. Ниже) выражается в дельте / год. Часто бывает полезно разделить это на количество дней в году, чтобы получить дельта-спад за день. Это использование довольно точно, когда количество дней, оставшихся до истечения опциона, велико. Когда срок действия опциона приближается к истечению, само очарование может быстро измениться, из-за чего оценки дельта-распада за целый день будут неточными.

Вомма

Вомма,^[4] волга,^[14] выпуклость Вега,^[14] или же ДвегаДвол^[14] измеряет чувствительность второго порядка к непостоянство. Vomma - это вторая производная от стоимости опциона по отношению к волатильности, или, другими словами, vomma измеряет скорость изменения к веге по мере изменения волатильности.

${\displaystyle {\text{Vomma}}={\frac {\partial {\mathcal {V}}}{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma ^{2}}}}$

При положительной вомме позиция станет длинной вегой, поскольку подразумеваемая волатильность увеличивается, а короткая вегета - по мере уменьшения, что может быть скальпировано аналогично длинной гамме. И изначально вегетативно-нейтральная позиция с длинной рвотой может быть построена из соотношения вариантов при разных ударах. Вомма положительна для опционов без денег, и изначально увеличивается с удалением от денег (но падает, когда вега падает). (В частности, vomma положительна, когда обычные члены d1 и d2 имеют один и тот же знак, что верно, когда d1 <0 или d2> 0.)

Вета

Вета^[15] или же DvegaDtime^[14] измеряет скорость изменения веги с течением времени. Вета - вторая производная функции ценности; один раз к волатильности и один раз ко времени.

${\displaystyle {\text{Veta}}={\frac {\partial {\mathcal {V}}}{\partial \tau }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial \tau }}}$

Обычно математический результат веты делят на 100-кратное количество дней в году, чтобы уменьшить значение до процентного изменения веги за один день.

Вера

Вера^[16] (иногда Рова)^[16] измеряет скорость изменения rho относительно волатильности. Вера - вторая производная функции цены; один раз для волатильности и один раз для процентной ставки.

${\displaystyle {\text{Vera}}={\frac {\partial \rho }{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial r}}}$

Слово «Вера» было придумано Р. Нарышкиным в начале 2012 года, когда эту чувствительность нужно было использовать на практике для оценки влияния изменений волатильности на родохеджирование, но в доступной литературе такого названия еще не было. «Vera» было выбрано так, чтобы звучать как комбинация Vega и Rho, соответствующих греков первого порядка. Это имя сейчас используется более широко, включая, например, Клен программное обеспечение для компьютерной алгебры (которое имеет функцию «BlackScholesVera» в своем финансовом пакете).

Греки третьего порядка

Скорость

Скорость^[4] измеряет скорость изменения гаммы по отношению к изменениям базовой цены.

${\displaystyle {\text{Speed}}={\frac {\partial \Gamma }{\partial S}}={\frac {\partial ^{3}V}{\partial S^{3}}}}$

Это также иногда называют гамма гаммы^[2]:799 или же DgammaDspot.^[12] Скорость является третьей производной функции стоимости по базовой спотовой цене. Скорость может быть важна для отслеживания, когда дельта-хеджирование или гамма-хеджирование портфеля.

Зомма

Зомма^[4] измеряет скорость изменения гаммы в зависимости от изменений волатильности.

${\displaystyle {\text{Zomma}}={\frac {\partial \Gamma }{\partial \sigma }}={\frac {\partial {\text{vanna}}}{\partial S}}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \sigma }}}$

Зомма также упоминается как DgammaDvol.^[12] Zomma - это третья производная от стоимости опциона, дважды по отношению к цене базового актива и один раз по волатильности. Zomma может быть полезной чувствительностью для мониторинга при поддержании портфеля с гамма-хеджированием, поскольку zomma поможет трейдеру предвидеть изменения эффективности хеджирования по мере изменения волатильности.

Цвет

Цвет,^{[12][примечание 1]} гамма-распад^[17] или же DgammaDtime^[12] измеряет скорость изменения гаммы с течением времени.

${\displaystyle {\text{Color}}={\frac {\partial \Gamma }{\partial \tau }}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \tau }}}$

Цвет - это производная третьего порядка от стоимости опциона, дважды по отношению к цене базового актива и один раз по времени. Цвет может быть важной чувствительностью, которую необходимо контролировать при ведении портфеля с гамма-хеджированием, поскольку он может помочь трейдеру предвидеть эффективность хеджирования с течением времени.

Математический результат формулы для цвета (см. Ниже) выражается в гамме / год. Часто бывает полезно разделить это на количество дней в году, чтобы получить изменение гаммы за день. Это использование довольно точно, когда количество дней, оставшихся до истечения опциона, велико. Когда срок действия опциона истекает, сам цвет может быстро измениться, что делает оценки изменения гаммы за целый день неточными.

Ultima

Ultima^[4] измеряет чувствительность vomma опциона к изменению волатильности.

${\displaystyle {\text{Ultima}}={\frac {\partial {\text{vomma}}}{\partial \sigma }}={\frac {\partial ^{3}V}{\partial \sigma ^{3}}}}$

Ultima также упоминается как ДвоммаДвол.^[4] Ultima - это производная третьего порядка от стоимости опциона к волатильности.

Греки за варианты с несколькими активами

Если стоимость производного инструмента зависит от двух или более подчиненные, его греки расширены, чтобы включить перекрестные эффекты между лежащими в основе.

Дельта корреляции измеряет чувствительность стоимости производного инструмента к изменению корреляции между базовыми активами.^[18] Он также широко известен как cega.^[19][20]

Перекрестная гамма измеряет скорость изменения дельты одного базового актива к изменению уровня другого базового актива.^[21]

Крест vanna измеряет скорость изменения веги в одном базовом активе из-за изменения уровня другого базового актива. Точно так же он измеряет скорость изменения дельты для второго базового актива из-за изменения волатильности первого базового актива.^[18]

Крест волга измеряет скорость изменения веги одного базового актива к изменению волатильности другого базового актива.^[21]

Формулы для европейского варианта греков

Смотрите также: Модель Блэка – Шоулза

Греки Европейские варианты (звонки и ставит ) под Модель Блэка – Шоулза рассчитываются следующим образом, где ${\displaystyle \phi }$ (фи) - это стандартный нормальный функция плотности вероятности и ${\displaystyle \Phi }$ это стандартный нормальный кумулятивная функция распределения. Обратите внимание, что формулы гаммы и веги одинаковы для коллов и путов.

Для данного:

• Цена акции ${\displaystyle S\,}$,
• Цена исполнения ${\displaystyle K\,}$,
• Безрисковая ставка ${\displaystyle r\,}$,
• Годовая дивидендная доходность ${\displaystyle q\,}$,
• Время до зрелости ${\displaystyle \tau =T-t\,}$ (представлены в виде доли одного года без единицы измерения), и
• Волатильность ${\displaystyle \sigma \,}$.

	Звонки	Ставит
справедливая стоимость (${\displaystyle V}$)	${\displaystyle Se^{-q\tau }\Phi (d_{1})-e^{-r\tau }K\Phi (d_{2})\,}$	${\displaystyle e^{-r\tau }K\Phi (-d_{2})-Se^{-q\tau }\Phi (-d_{1})\,}$
дельта (${\displaystyle \Delta }$)	${\displaystyle e^{-q\tau }\Phi (d_{1})\,}$	${\displaystyle -e^{-q\tau }\Phi (-d_{1})\,}$
Вега (${\displaystyle {\mathcal {V}}}$)	${\displaystyle Se^{-q\tau }\phi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\phi (d_{2}){\sqrt {\tau }}\,}$
тета (${\displaystyle \Theta }$)	${\displaystyle -e^{-q\tau }{\frac {S\phi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+qSe^{-q\tau }\Phi (d_{1})\,}$	${\displaystyle -e^{-q\tau }{\frac {S\phi (-d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-qSe^{-q\tau }\Phi (-d_{1})\,}$
ро (${\displaystyle \rho }$)	${\displaystyle K\tau e^{-r\tau }\Phi (d_{2})\,}$	${\displaystyle -K\tau e^{-r\tau }\Phi (-d_{2})\,}$
лямбда (${\displaystyle \lambda }$)	${\displaystyle \Delta {\frac {S}{V}}\,}$
гамма (${\displaystyle \Gamma }$)	${\displaystyle e^{-q\tau }{\frac {\phi (d_{1})}{S\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\phi (d_{2})}{S^{2}\sigma {\sqrt {\tau }}}}\,}$
Vanna	${\displaystyle -e^{-q\tau }\phi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{S}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,}$
очарование	${\displaystyle qe^{-q\tau }\Phi (d_{1})-e^{-q\tau }\phi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,}$	${\displaystyle -qe^{-q\tau }\Phi (-d_{1})-e^{-q\tau }\phi (d_{1}){\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{2\tau \sigma {\sqrt {\tau }}}}\,}$
рвота	${\displaystyle Se^{-q\tau }\phi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,}$
вета	${\displaystyle -Se^{-q\tau }\phi (d_{1}){\sqrt {\tau }}\left[q+{\frac {\left(r-q\right)d_{1}}{\sigma {\sqrt {\tau }}}}-{\frac {1+d_{1}d_{2}}{2\tau }}\right]\,}$
скорость	${\displaystyle -e^{-q\tau }{\frac {\phi (d_{1})}{S^{2}\sigma {\sqrt {\tau }}}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)=-{\frac {\Gamma }{S}}\left({\frac {d_{1}}{\sigma {\sqrt {\tau }}}}+1\right)\,}$
зомма	${\displaystyle e^{-q\tau }{\frac {\phi (d_{1})\left(d_{1}d_{2}-1\right)}{S\sigma ^{2}{\sqrt {\tau }}}}=\Gamma \cdot \left({\frac {d_{1}d_{2}-1}{\sigma }}\right)\,}$
цвет	${\displaystyle -e^{-q\tau }{\frac {\phi (d_{1})}{2S\tau \sigma {\sqrt {\tau }}}}\left[2q\tau +1+{\frac {2(r-q)\tau -d_{2}\sigma {\sqrt {\tau }}}{\sigma {\sqrt {\tau }}}}d_{1}\right]\,}$
ультима	${\displaystyle {\frac {-{\mathcal {V}}}{\sigma ^{2}}}\left[d_{1}d_{2}(1-d_{1}d_{2})+d_{1}^{2}+d_{2}^{2}\right]}$
двойная дельта	${\displaystyle -e^{-r\tau }\Phi (d_{2})\,}$	${\displaystyle e^{-r\tau }\Phi (-d_{2})\,}$
двойная гамма	${\displaystyle e^{-r\tau }{\frac {\phi (d_{2})}{K\sigma {\sqrt {\tau }}}}\,}$

куда

${\displaystyle d_{1}={\frac {\ln(S/K)+(r-q+\sigma ^{2}/2)\tau }{\sigma {\sqrt {\tau }}}}}$

${\displaystyle d_{2}={\frac {\ln(S/K)+(r-q-\sigma ^{2}/2)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}}$

${\displaystyle \phi (x)={\frac {e^{-{\frac {x^{2}}{2}}}}{\sqrt {2\pi }}}}$

${\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {y^{2}}{2}}}\,dy=1-{\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {y^{2}}{2}}}\,dy}$

Под Черная модель (обычно используется для товаров и опционов на фьючерсы) греков можно рассчитать следующим образом:

	Звонки	Ставит
справедливая стоимость (${\displaystyle V}$)	${\displaystyle e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\ }$	${\displaystyle e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,}$
дельта (${\displaystyle \Delta }$) ${\displaystyle =\partial V/\partial F}$	${\displaystyle e^{-r\tau }\Phi (d_{1})\,}$	${\displaystyle -e^{-r\tau }\Phi (-d_{1})\,}$
Вега (${\displaystyle {\mathcal {V}}}$)	${\displaystyle Fe^{-r\tau }\phi (d_{1}){\sqrt {\tau }}=Ke^{-r\tau }\phi (d_{2}){\sqrt {\tau }}\,}$ (*)
тета (${\displaystyle \Theta }$)	${\displaystyle -{\frac {Fe^{-r\tau }\phi (d_{1})\sigma }{2{\sqrt {\tau }}}}-rKe^{-r\tau }\Phi (d_{2})+rFe^{-r\tau }\Phi (d_{1})\,}$	${\displaystyle -{\frac {Fe^{-r\tau }\phi (-d_{1})\sigma }{2{\sqrt {\tau }}}}+rKe^{-r\tau }\Phi (-d_{2})-rFe^{-r\tau }\Phi (-d_{1})\,}$
ро (${\displaystyle \rho }$)	${\displaystyle -\tau e^{-r\tau }[F\Phi (d_{1})-K\Phi (d_{2})]\ }$	${\displaystyle -\tau e^{-r\tau }[K\Phi (-d_{2})-F\Phi (-d_{1})]\,}$
гамма (${\displaystyle \Gamma }$)${\displaystyle ={\partial ^{2}V \over \partial F^{2}}}$	${\displaystyle e^{-r\tau }{\frac {\phi (d_{1})}{F\sigma {\sqrt {\tau }}}}=Ke^{-r\tau }{\frac {\phi (d_{2})}{F^{2}\sigma {\sqrt {\tau }}}}\,}$ (*)
Vanna${\displaystyle ={\frac {\partial ^{2}V}{\partial F\partial \sigma }}}$	${\displaystyle -e^{-r\tau }\phi (d_{1}){\frac {d_{2}}{\sigma }}\,={\frac {\mathcal {V}}{F}}\left[1-{\frac {d_{1}}{\sigma {\sqrt {\tau }}}}\right]\,}$
рвота	${\displaystyle Fe^{-r\tau }\phi (d_{1}){\sqrt {\tau }}{\frac {d_{1}d_{2}}{\sigma }}={\mathcal {V}}{\frac {d_{1}d_{2}}{\sigma }}\,}$

куда

${\displaystyle d_{1}={\frac {\ln(F/K)+(\sigma ^{2}/2)\tau }{\sigma {\sqrt {\tau }}}}}$

${\displaystyle d_{2}={\frac {\ln(F/K)-(\sigma ^{2}/2)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}}$

(*) Можно показать, что ${\displaystyle F\phi (d_{1})=K\phi (d_{2})}$

Связанные меры

Некоторые соответствующие меры риска производных финансовых инструментов перечислены ниже.

Продолжительность и выпуклость связи

Основные статьи: Срок действия облигации и Связь выпуклости

При торговле ценными бумагами с фиксированным доходом (облигациями) различные меры дюрация облигации используются аналогично дельте опциона. Ближайший аналог дельты - DV01, то есть удешевление (в денежных единицах) при увеличении на один базисная точка (т.е. 0,01% годовых) в доходности (доходность является базовой переменной).

Аналогично лямбде измененная продолжительность, какой процент изменение рыночной цены облигации (й) на единица измерения изменение доходности (т. е. эквивалентно DV01, деленному на рыночную цену). В отличие от лямбды, которая является эластичность (процентное изменение вывода для процентного изменения ввода), вместо этого измененная продолжительность полу-упругость - процентное изменение выпуска для единица измерения изменение ввода.

Связь выпуклости является мерой чувствительности продолжительности к изменениям в процентные ставки, то вторая производная цены облигации по отношению к процентным ставкам (дюрация - первая производная). В целом, чем выше выпуклость, тем более чувствительна цена облигации к изменению процентных ставок. Выпуклость связки - одна из самых основных и широко используемых форм выпуклость в финансах.

Для связи с встроенный вариант, стандарт доходность к погашению Основанные здесь расчеты не учитывают, как изменения процентных ставок повлияют на денежные потоки из-за исполнения опциона. Чтобы решить эту проблему, эффективная продолжительность и эффективная выпуклость вводятся. Эти значения обычно рассчитываются с использованием древовидной модели, построенной для всей кривой доходности (в отличие от единственной доходности к погашению), и, следовательно, фиксируют поведение исполнения в каждый момент срока действия опциона как функцию как времени, так и процентных ставок. ; видеть Решеточная модель (финансы) # Деривативы по процентной ставке.

Бета

Основная статья: Бета (финансы)

В бета (β) акции или же портфолио - это число, описывающее волатильность актива по отношению к волатильности эталона, с которым сравнивается данный актив. Этот эталонный показатель обычно представляет собой общий финансовый рынок и часто оценивается с использованием репрезентативных индексы, такой как S&P 500.

Бета актива равна нулю, если его доходность изменяется независимо от изменений доходности рынка. Положительная бета означает, что доходность актива обычно соответствует доходности рынка в том смысле, что оба они имеют тенденцию быть выше своих соответствующих средних значений вместе, или оба имеют тенденцию быть ниже своих соответствующих средних значений вместе. Отрицательная бета означает, что доходность актива обычно движется в противоположном направлении от доходности рынка: одна будет обычно выше своего среднего значения, когда другое ниже среднего.

Фугит

Основная статья: Фугит

В фугит это ожидаемое время для исполнения американского или бермудского опциона. Его полезно вычислить для целей хеджирования - например, можно представить потоки американского обмен как потоки свопа, начинающиеся с фугита, умноженного на дельту, затем используйте их для вычисления чувствительности.

Смотрите также

• Альфа (финансы)
• Бета (финансы)
• Дельта-нейтральный
• Греческие буквы, используемые в математике, науке и технике
• Цены на Ванна – Волга

Примечания

1. Этот автор видел это только в британском написании «цвет», но написал это здесь, в американском правописании, чтобы оно соответствовало стилю существующей статьи.

Рекомендации

1. Бэнкс, Эрик; Сигел, Пол (2006). Справочник по опционным приложениям: методы хеджирования и спекуляции для профессиональных инвесторов. McGraw-Hill Professional. п. 263. ISBN  9780071453158.
2. Макмиллан, Лоуренс Г. (1993). Варианты как стратегическая инвестиция (3-е изд.). Нью-Йоркский институт финансов. ISBN  978-0-13-636002-5.
3. Крисс, Нил (1996). Блэк – Шоулз и другие: модели ценообразования опционов. McGraw-Hill Professional. п.308. ISBN  9780786310258.
4. Хауг, Эспен Гарднер (2007). Полное руководство по формулам ценообразования опционов. McGraw-Hill Professional. ISBN  9780071389976.
5. Сума, Джон. "Греки опционов: Дельта Риск и Вознаграждение". Получено 7 янв 2010.
6. Штайнер, Боб (2013). Освоение финансовых расчетов (3-е изд.). Пирсон Великобритания. ISBN  9780273750604.
7. Халл, Джон С. (1993). Опционы, фьючерсы и другие производные ценные бумаги (2-е изд.). Prentice-Hall. ISBN  9780136390145.
8. Омега - Инвестопедия
9. Де Шпигелеер, Ян; Схоутенс, Вим (2015). Справочник конвертируемых облигаций: ценообразование, стратегии и управление рисками. Джон Уайли и сыновья. С. 255, 269–270. ISBN  9780470689684.
10. Виллетт, Джефф (28 мая 2014 г.). «Понимание того, как гамма влияет на дельту». www.traderbrains.com. Получено 2014-03-07.
11. Виллетт, Джефф (28 мая 2014 г.). "Почему гамма длинных опционов положительна". www.traderbrains.com. Получено 2014-03-07.
12. Хауг, Эспен Гардер (2003), "Знай свое оружие, часть 1" (PDF), Журнал Wilmott (Май 2003 г.): 49–57
13. Деривативы - Delta Decay - Финансовая энциклопедия
14. Хауг, Эспен Гардер (2003), "Знай свое оружие, часть 2", Журнал Wilmott (Июль 2003 г.): 43–57
15. Пиерино Урсоне. Как рассчитать цены опционов и их греки: исследование модели Блэка-Шоулза от Дельты до Веги. Джон Вили и сыновья. 2015 г.
16. Деривативы - Греки второго порядка - Финансовая энциклопедия
17. Деривативы - Греки - Финансовая энциклопедия
18. «Греки за опционы на несколько активов». Получено 24 января 2017.
19. «Корреляционный риск». Получено 22 марта 2018.
20. «Варианты смены горных хребтов, оценка и риски / Анализ эффективности». Получено 22 марта 2018.
21. Фенглер, Маттиас; Швенднер, Питер. «Премия за корреляционный риск для опционов на несколько активов» (PDF).

внешняя ссылка

Теория

• Дельта, Гамма, ГаммаП, Гамма-симметрия, Ванна, Скорость, Очарование, Гамма седла: Варианты ванили - Эспен Хауг,
• Волга, Ванна, Скорость, Очарование, Цвет: Ванильные варианты - Уве Виступ, Ванильные варианты - Уве Виступ

Пошаговые математические выводы опционов греков

• Расчет стоимости звонка в европейском стиле
• Производное от европейской ванильной дельты вызова
• Выведение европейской ванильной гаммы
• Получение скорости европейского ванильного вызова
• Производное от European Vanilla Call Vega
• От слова European Vanilla Call Volga
• Производное от European Vanilla Call Vanna как производного от Vega в отношении базового
• Получение европейской Vanilla Call Vanna как производной от дельты в отношении волатильности
• Производное от европейского ванильного Call Theta
• Производное от европейского ванильного Call Rho
• Выведение цены европейского ванильного пут
• Производное от European Vanilla Put Delta
• Производное от European Vanilla Put Gamma
• Производное от European Vanilla Put Speed
• Производное от European Vanilla Put Vega
• Производное от European Vanilla Put Volga
• Производное от европейской ванили (European Vanilla) .Позволяет использовать Vanna как производную от Vega по отношению к основному
• Производная от европейской ванили, поставив Ванну как производную от дельты в отношении волатильности
• Производное от European Vanilla Put Theta
• Производное от European Vanilla Put Rho

Онлайн-инструменты

• Графики поверхности греков Блэка-Шоулза, Крис Мюррей
• Онлайн-калькулятор цен опционов в реальном времени и калькулятор греков при нормальном распределении базового актива, Разван Паскалау, Univ. Алабамы
• Инструмент для расчета греков на основе Excel, бесплатный лист Excel, предоставленный Pristine