Неявный метод переменного направления - Alternating direction implicit method

В числовая линейная алгебра, то Неявный метод переменного направления (ADI) это итерационный метод, используемый для решения Сильвестр матричные уравнения. Это популярный метод решения больших матричных уравнений, возникающих в теория систем и контроль,^[1] и могут быть сформулированы для построения решений в факторизованной форме с эффективным использованием памяти.^[2][3] Он также используется для численного решения параболический и эллиптический уравнения в частных производных, и это классический метод, используемый для моделирования теплопроводность и решение уравнение диффузии в двух или более измерениях.^[4] Это пример разделение операторов метод.^[5]

ADI для матричных уравнений

Метод

Метод ADI - это двухэтапный итерационный процесс, который поочередно обновляет пространства столбцов и строк приближенного решения для ${displaystyle AX-XB=C}$. Одна итерация ADI состоит из следующих шагов:^[6]

1. Решите для ${displaystyle X^{(j+1/2)}}$, где ${displaystyle left(A-eta _{j+1}Iight)X^{(j+1/2)}=X^{(j)}left(B-eta _{j+1}Iight)+C.}$

2. Решите для ${displaystyle X^{(j+1)}}$, где ${displaystyle X^{(j+1)}left(B-alpha _{j+1}Iight)=left(A-alpha _{j+1}Iight)X^{(j+1/2)}-C}$.

Число ${displaystyle (alpha _{j+1},eta _{j+1})}$ называются параметрами сдвига, и сходимость сильно зависит от выбора этих параметров.^[7][8] Выполнить ${displaystyle K}$ итерации ADI, первоначальное предположение ${displaystyle X^{(0)}}$ требуется, а также ${displaystyle K}$ параметры смены, ${displaystyle {(alpha _{j},eta _{j})}_{j=1}^{K}}$.

Когда использовать ADI

Если ${displaystyle Ain mathbb {C} ^{m imes m}}$ и ${displaystyle Bin mathbb {C} ^{n imes n}}$, тогда ${displaystyle AX-XB=C}$ можно решить прямо в ${displaystyle {mathcal {O}}(m^{3}+n^{3})}$ с помощью метода Бартельса-Стюарта.^[9] Поэтому использование ADI выгодно только тогда, когда умножение матрицы на вектор и линейные решения включают ${displaystyle A}$ и ${displaystyle B}$ может применяться дешево.

Уравнение ${displaystyle AX-XB=C}$ имеет единственное решение тогда и только тогда, когда ${displaystyle sigma (A)cap sigma (B)=emptyset }$, где ${displaystyle sigma (M)}$ это спектр из ${displaystyle M}$.^[1] Однако метод ADI особенно хорошо работает, когда ${displaystyle sigma (A)}$ и ${displaystyle sigma (B)}$ хорошо разделены, и ${displaystyle A}$ и ${displaystyle B}$ находятся нормальные матрицы. Этим предположениям удовлетворяет, например, уравнение Ляпунова ${displaystyle AX+XA^{*}=C}$ когда ${displaystyle A}$ является положительно определенный. При этих предположениях параметры сдвига, близкие к оптимальным, известны для нескольких вариантов выбора ${displaystyle A}$ и ${displaystyle B}$.^[7][8] Кроме того, могут быть вычислены априорные границы ошибок, что устраняет необходимость в мониторинге остаточной ошибки при реализации.

Метод ADI все еще может применяться, когда вышеприведенные предположения не выполняются. Использование неоптимальных параметров сдвига может отрицательно повлиять на сходимость,^[1] и на сходимость также влияет ненормальность ${displaystyle A}$ или ${displaystyle B}$ (иногда выгодно).^[10] Крыловское подпространство методы, такие как Рациональный метод подпространств Крылова,^[11] обычно сходятся быстрее, чем ADI в этой настройке,^[1][3] и это привело к развитию гибридных методов ADI-проекции.^[3]

Выбор параметра сдвига и уравнение ошибки ADI

Задача поиска хороших параметров сдвига нетривиальна. Эту проблему можно понять, изучив уравнение ошибки ADI. После ${displaystyle K}$ итераций ошибка определяется выражением

${displaystyle X-X^{(K)}=prod _{j=1}^{K}{frac {(A-alpha _{j}I)}{(A-eta _{j}I)}}left(X-X^{(0)}ight)prod _{j=1}^{K}{frac {(B-eta _{j}I)}{(B-alpha _{j}I)}}.}$

Выбор ${displaystyle X^{(0)}=0}$ приводит к следующей границе относительной ошибки:

${displaystyle {frac {left|X-X^{(K)}ight|_{2}}{|X|_{2}}}leq |r_{K}(A)|_{2}|r_{K}(B)^{-1}|_{2},quad r_{K}(M)=prod _{j=1}^{K}{frac {(M-alpha _{j}I)}{(M-eta _{j}I)}}.}$

где ${displaystyle |cdot |_{2}}$ это норма оператора. Идеальный набор параметров смены ${displaystyle {(alpha _{j},eta _{j})}_{j=1}^{K}}$ определяет рациональная функция ${displaystyle r_{K}}$ что минимизирует количество ${displaystyle |r_{K}(A)|_{2}|r_{K}(B)^{-1}|_{2}}$. Если ${displaystyle A}$ и ${displaystyle B}$ находятся нормальные матрицы и имеют собственные разложения ${displaystyle A=V_{A}Lambda _{A}V_{A}^{*}}$ и ${displaystyle B=V_{B}Lambda _{B}V_{B}^{*}}$, тогда

${displaystyle |r_{K}(A)|_{2}|r_{K}(B)^{-1}|_{2}=|r_{K}(Lambda _{A})|_{2}|r_{K}(Lambda _{B})^{-1}|_{2}}$.

Практически оптимальные параметры смены

В некоторых случаях известны близкие к оптимальным параметры сдвига, например, когда ${displaystyle Lambda _{A}subset [a,b]}$ и ${displaystyle Lambda _{B}subset [c,d]}$, где ${displaystyle [a,b]}$ и ${displaystyle [c,d]}$ непересекающиеся интервалы на прямой.^[7][8] В Уравнение Ляпунова ${displaystyle AX+XA^{*}=C}$, например, удовлетворяет этим предположениям, когда ${displaystyle A}$ является положительно определенный. В этом случае параметры сдвига можно выразить в замкнутой форме с помощью эллиптические интегралы, и легко вычисляется численно.

В более общем смысле, если замкнутые непересекающиеся множества ${displaystyle E}$ и ${displaystyle F}$, где ${displaystyle Lambda _{A}subset E}$ и ${displaystyle Lambda _{B}subset F}$, известны, задача выбора оптимального параметра сдвига приближенно решается путем нахождения экстремальной рациональной функции, которая принимает значение

${displaystyle Z_{K}(E,F):=inf _{r}{frac {sup _{zin E}|r(z)|}{inf _{zin F}|r(z)|}},}$

где нижняя грань берется по всем рациональным функциям степени ${displaystyle (K,K)}$.^[8] Эта проблема аппроксимации связана с несколькими результатами в теория потенциала,^[12][13] и был решен Золотарев в 1877 г. для ${displaystyle E}$ = [a, b] и ${displaystyle F=-E.}$^[14] Решение также известно, когда ${displaystyle E}$ и ${displaystyle F}$ непересекающиеся диски на комплексной плоскости.^[15]

Стратегии эвристического сдвига параметров

Когда меньше известно о ${displaystyle sigma (A)}$ и ${displaystyle sigma (B)}$, или когда ${displaystyle A}$ или ${displaystyle B}$ являются ненормальными матрицами, может оказаться невозможным найти близкие к оптимальным параметры сдвига. В этой настройке можно использовать различные стратегии для создания хороших параметров переключения передач. К ним относятся стратегии, основанные на асимптотических результатах в теории потенциала,^[16] используя значения Ритца матриц ${displaystyle A}$, ${displaystyle A^{-1}}$, ${displaystyle B}$, и ${displaystyle B^{-1}}$ сформулировать жадный подход,^[17] и циклические методы, в которых один и тот же небольшой набор параметров сдвига повторно используется до тех пор, пока не будет соблюден допуск сходимости.^[17][10] Когда один и тот же параметр сдвига используется на каждой итерации, ADI эквивалентен алгоритму, называемому методом Смита.^[18]

Фактор ADI

Во многих приложениях ${displaystyle A}$ и ${displaystyle B}$ очень большие, разреженные матрицы и ${displaystyle C}$ можно разложить на множители как ${displaystyle C=C_{1}C_{2}^{*}}$, где ${displaystyle C_{1}in mathbb {C} ^{m imes r},C_{2}in mathbb {C} ^{n imes r}}$, с участием ${displaystyle r=1,2}$.^[1] В таких условиях хранение потенциально плотной матрицы может оказаться невозможным. ${displaystyle X}$ явно. Вариант ADI, называемый факторизованным ADI,^[3][2] можно использовать для вычисления ${displaystyle ZY^{*}}$, где ${displaystyle Xapprox ZY^{*}}$. Эффективность факторного ADI зависит от того, ${displaystyle X}$ хорошо аппроксимируется матрицей низкого ранга. Это, как известно, верно при различных предположениях о ${displaystyle A}$ и ${displaystyle B}$.^[10][8]

ADI для параболических уравнений

Исторически метод ADI был разработан для решения двумерного уравнения диффузии в квадратной области с использованием конечных разностей.^[4] В отличие от ADI для матричных уравнений, ADI для параболических уравнений не требует выбора параметров сдвига, поскольку сдвиг, появляющийся на каждой итерации, определяется такими параметрами, как временной шаг, коэффициент диффузии и шаг сетки. Связь с ADI в матричных уравнениях можно наблюдать, если рассмотреть действие итерации ADI на систему в установившемся состоянии.

Пример: двумерное уравнение диффузии

Трафаретная фигура для неявного метода переменного направления в конечно-разностных уравнениях

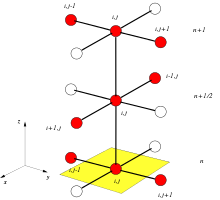
Традиционным методом численного решения уравнения теплопроводности является метод Метод Кранка – Николсона. Этот метод приводит к очень сложной системе уравнений в нескольких измерениях, решение которых требует больших затрат. Преимущество метода ADI заключается в том, что уравнения, которые необходимо решать на каждом этапе, имеют более простую структуру и могут быть эффективно решены с помощью алгоритм трехдиагональной матрицы.

Рассмотрим линейное уравнение диффузии в двух измерениях:

${displaystyle {partial u over partial t}=left({partial ^{2}u over partial x^{2}}+{partial ^{2}u over partial y^{2}}ight)=(u_{xx}+u_{yy})}$

Неявный метод Кранка – Николсона дает следующее уравнение конечных разностей:

${displaystyle {u_{ij}^{n+1}-u_{ij}^{n} over Delta t}={1 over 2(Delta x)^{2}}left(delta _{x}^{2}+delta _{y}^{2}ight)left(u_{ij}^{n+1}+u_{ij}^{n}ight)}$

где:

${displaystyle Delta x=Delta y}$

и ${displaystyle delta _{p}^{2}}$ - центральный второй разностный оператор для п-я координата

${displaystyle delta _{p}^{2}u_{ij}=u_{ij+e_{p}}-2u_{ij}+u_{ij-e_{p}}}$

с участием ${displaystyle e_{p}=10}$ или ${displaystyle 01}$ для ${displaystyle p=x}$ или ${displaystyle y}$ соответственно (и ${displaystyle ij}$ сокращение для точек решетки ${displaystyle (i,j)}$).

После выполнения анализ устойчивости, можно показать, что этот метод будет устойчивым для любых ${displaystyle Delta t}$.

Недостатком метода Кранка – Николсона является то, что матрица в приведенном выше уравнении имеет вид полосатый с шириной полосы, как правило, довольно большой. Это делает прямое решение проблемы система линейных уравнений довольно затратно (хотя существуют эффективные приближенные решения, например, использование метод сопряженных градиентов предварительно подготовленный с неполная факторизация Холецкого ).

Идея метода ADI состоит в том, чтобы разделить конечно-разностные уравнения на два, одно с Икс-производная берется неявно, а следующая с y-производная взята неявно,

${displaystyle {u_{ij}^{n+1/2}-u_{ij}^{n} over Delta t/2}={left(delta _{x}^{2}u_{ij}^{n+1/2}+delta _{y}^{2}u_{ij}^{n}ight) over Delta x^{2}}}$

${displaystyle {u_{ij}^{n+1}-u_{ij}^{n+1/2} over Delta t/2}={left(delta _{x}^{2}u_{ij}^{n+1/2}+delta _{y}^{2}u_{ij}^{n+1}ight) over Delta y^{2}}}$

Используемая система уравнений имеет вид симметричный и трехдиагональный (с полосой пропускания 3), и обычно решается с использованием алгоритм трехдиагональной матрицы.

Можно показать, что этот метод безусловно устойчив и имеет второй порядок во времени и пространстве.^[19] Существуют более усовершенствованные методы ADI, такие как методы Дугласа,^[20] или метод f-фактора^[21] который можно использовать для трех или более измерений.

Обобщения

Использование метода ADI в качестве разделение операторов Схема может быть обобщена. То есть мы можем рассматривать общие эволюционные уравнения

${displaystyle {dot {u}}=F_{1}u+F_{2}u,}$

где ${displaystyle F_{1}}$ и ${displaystyle F_{2}}$ являются (возможно, нелинейными) операторами, определенными в банаховом пространстве.^[22][23] В приведенном выше примере распространения мы имеем ${displaystyle F_{1}={partial ^{2} over partial x^{2}}}$ и ${displaystyle F_{2}={partial ^{2} over partial y^{2}}}$.

Фундаментальный ADI (FADI)

Упрощение ADI до FADI

Можно упростить традиционный метод ADI до метода Fundamental ADI, который имеет только аналогичные операторы в левой части и не содержит операторов в правой части. Это можно рассматривать как фундаментальную (базовую) схему метода ADI,^[24][25] без дополнительных операторов (подлежащих сокращению) в правой части, в отличие от большинства традиционных неявных методов, которые обычно состоят из операторов в обеих частях уравнений. Метод FADI позволяет получить более простые, краткие и эффективные уравнения обновления без ухудшения точности обычного метода ADI.

Отношения к другим неявным методам

Многие классические неявные методы Пичмана-Рачфорда, Дугласа-Ганна, Д'Яконова, Луча-Уорминга, Крэнка-Николсона и т. Д. Могут быть упрощены до фундаментальных неявных схем с правыми частями без операторов.^[25] В своих основных формах метод FADI временной точности второго порядка может быть тесно связан с фундаментальным локально-одномерным методом (FLOD), который может быть повышен до временного порядка второго порядка, например, для трехмерных уравнений Максвелла. ^[26][27] в вычислительная электромагнетизм. Для двумерных и трехмерных уравнений теплопроводности и диффузии методы FADI и FLOD могут быть реализованы более простым, более эффективным и стабильным образом по сравнению с их традиционными методами. ^[28][29]

использованная литература

1. Симончини, В. (2016). «Вычислительные методы для линейных матричных уравнений». SIAM Обзор. 58 (3): 377–441. Дои:10.1137/130912839. ISSN  0036-1445. S2CID  17271167.
2. Ли, Цзин-Ребекка; Белый, Джейкоб (2002). "Решение уравнений Ляпунова низкого ранга". Журнал SIAM по матричному анализу и приложениям. 24 (1): 260–280. Дои:10.1137 / s0895479801384937. ISSN  0895-4798.
3. Беннер, Питер; Ли, Рен-Цан; Трухар, Нинослав (2009). «О методе ADI для уравнений Сильвестра». Журнал вычислительной и прикладной математики. 233 (4): 1035–1045. Bibcode:2009JCoAM.233.1035B. Дои:10.1016 / j.cam.2009.08.108. ISSN  0377-0427.
4. Peaceman, D. W .; Рачфорд-младший, Х. Х. (1955), "Численное решение параболических и эллиптических дифференциальных уравнений", Журнал Общества промышленной и прикладной математики, 3 (1): 28–41, Дои:10.1137/0103003, HDL:10338.dmlcz / 135399, Г-Н  0071874.
5. *Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, ВР (2007). «Раздел 20.3.3. Общие методы разделения операторов». Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-88068-8.
6. Wachspress, Юджин Л. (2008). "След к решению уравнения Ляпунова". Компьютеры и математика с приложениями. 55 (8): 1653–1659. Дои:10.1016 / j.camwa.2007.04.048. ISSN  0898-1221.
7. Лу, Ан; Wachspress, E.L. (1991). «Решение уравнений Ляпунова неявной итерацией с переменным направлением». Компьютеры и математика с приложениями. 21 (9): 43–58. Дои:10.1016 / 0898-1221 (91) 90124-м. ISSN  0898-1221.
8. Беккерманн, Бернхард; Таунсенд, Алекс (2017). «Об особых значениях матриц со структурой смещения». Журнал SIAM по матричному анализу и приложениям. 38 (4): 1227–1248. arXiv:1609.09494. Дои:10.1137 / 16m1096426. ISSN  0895-4798.
9. Голуб, Г. (1989). Матричные вычисления. Ван Лоан, С (Четвертое изд.). Балтимор: Университет Джона Хопкинса. ISBN  1421407949. OCLC  824733531.
10. Сабино, Дж (2007). Решение крупномасштабных уравнений Ляпунова блочно-модифицированным методом Смита. PhD Diss., Rice Univ. (Тезис). HDL:1911/20641.
11. Друскин, В .; Симончини, В. (2011). «Адаптивные рациональные подпространства Крылова для крупномасштабных динамических систем». Письма о системах и управлении. 60 (8): 546–560. Дои:10.1016 / j.sysconle.2011.04.013. ISSN  0167-6911.
12. 1944-, Сафф, Э. Б. (11 ноября 2013 г.). Логарифмические потенциалы с внешними полями. Тотик, В. Берлин. ISBN  9783662033296. OCLC  883382758.
13. Гончар, А.А. (1969). «Проблемы Золотарева, связанные с рациональными функциями». Мат. Сб. (Н.С.). 78 (120):4 (4): 640–654. Bibcode:1969СбМат ... 7..623Г. Дои:10.1070 / SM1969v007n04ABEH001107.
14. Золотарев, Д. (1877). «Применение эллиптических функций к вопросам о функциях, наименее и наиболее отклоняющихся от нуля». Зап. Imp. Акад. Наук. Санкт-Петербург. 30: 1–59.
15. Старке, Герхард (июль 1992 г.). «Околоокруглость для рациональной задачи Золотарева в комплексной плоскости». Журнал теории приближений. 70 (1): 115–130. Дои:10.1016 / 0021-9045 (92) 90059-в.. ISSN  0021-9045.
16. Старке, Герхард (июнь 1993). «Точки Фейера-Уолша для рациональных функций и их использование в итерационном методе ADI». Журнал вычислительной и прикладной математики. 46 (1–2): 129–141. Дои:10.1016 / 0377-0427 (93) 90291-я. ISSN  0377-0427.
17. Пенцл, Тило (январь 1999 г.). "Циклический метод Смита низкого ранга для больших разреженных уравнений Ляпунова". Журнал SIAM по научным вычислениям. 21 (4): 1401–1418. Дои:10.1137 / s1064827598347666. ISSN  1064-8275.
18. Смит, Р. А. (январь 1968 г.). «Матричное уравнение XA + BX = C». Журнал SIAM по прикладной математике. 16 (1): 198–201. Дои:10.1137/0116017. ISSN  0036-1399.
19. Дуглас-младший, Дж. (1955), "О численном интегрировании u_хх+ ты_гг= u_т неявными методами », Журнал Общества промышленной и прикладной математики, 3: 42–65, Г-Н  0071875.
20. Дуглас мл., Джим (1962), "Методы переменного направления для трех пространственных переменных", Numerische Mathematik, 4 (1): 41–63, Дои:10.1007 / BF01386295, ISSN  0029-599X.
21. Chang, M. J .; Chow, L.C .; Чанг, В. С. (1991), «Улучшенный неявный метод переменного направления для решения нестационарных трехмерных задач диффузии тепла», Числовой теплообмен, часть B: основы, 19 (1): 69–84, Bibcode:1991НХТБ ... 19 ... 69С, Дои:10.1080/10407799108944957, ISSN  1040-7790.
22. Хундсдорфер, Виллем; Вервер, янв (2003). Численное решение нестационарных уравнений адвекции-диффузии-реакции. Берлин, Гейдельберг: Springer Berlin Heidelberg. ISBN  978-3-662-09017-6.
23. Lions, P. L .; Мерсье, Б. (декабрь 1979 г.). «Алгоритмы расщепления суммы двух нелинейных операторов». Журнал SIAM по численному анализу. 16 (6): 964–979. Bibcode:1979SJNA ... 16..964L. Дои:10.1137/0716071.
24. Тан, Э. Л. (2007). «Эффективный алгоритм для безусловно стабильного трехмерного метода ADI-FDTD» (PDF). Письма IEEE о микроволновых и беспроводных компонентах. 17 (1): 7–9. Дои:10.1109 / LMWC.2006.887239.
25. Тан, Э. Л. (2008). «Основные схемы для эффективных безоговорочно стабильных неявных конечно-разностных методов во временной области» (PDF). Транзакции IEEE по антеннам и распространению. 56 (1): 170–177. Дои:10.1109 / TAP.2007.913089.
26. Тан, Э. Л. (2007). «Безусловно устойчивый метод LOD-FDTD для трехмерных уравнений Максвелла» (PDF). Письма IEEE о микроволновых и беспроводных компонентах. 17 (2): 85–87. Дои:10.1109 / LMWC.2006.890166.
27. Gan, T. H .; Тан, Э. Л. (2013). «Безоговорочно стабильный фундаментальный метод LOD-FDTD с временной точностью второго порядка и соответствующей дивергенцией» (PDF). Транзакции IEEE по антеннам и распространению. 61 (5): 2630–2638. Дои:10.1109 / TAP.2013.2242036.
28. Tay, W. C .; Tan, E. L .; Хех, Д. Ю. (2014). «Фундаментальный локально-одномерный метод трехмерного теплового моделирования». Сделки IEICE по электронике. E-97-C (7): 636–644. Дои:10.1587 / transele.E97.C.636.
29. Heh, D. Y .; Tan, E. L .; Тай, У. К. (2016). «Неявный метод быстрого изменения направления для эффективного теплового моделирования переходных процессов в интегральных схемах». Международный журнал численного моделирования: электронные сети, устройства и поля. 29 (1): 93–108. Дои:10.1002 / jnm.2049.