Станислав Улам - Stanislaw Ulam

Станислав Улам
Станислав Улам
Родился	Станислав Марцин Улам (1909-04-03)3 апреля 1909 г. Лемберг, Австро-Венгрия (сейчас же Львов, Украина )
Умер	13 мая 1984 г.(1984-05-13) (в возрасте 75 лет) Санта-Фе, Нью-Мексико, США
Национальность	Польский
Гражданство	Польша, США (натурализованы в 1941 г.)
Образование	Львовский политехнический институт, Вторая Польская Республика
Известен	Математические постановки в областях Физика, Информатика, и Биология Дизайн Теллера – Улама Метод Монте-Карло Проблема Ферми – Паста – Улама – Цингоу Ядерный импульсный двигатель
Научная карьера
Поля	Математика
Учреждения	Институт перспективных исследований Гарвардский университет Университет Висконсина Лос-Аламосская национальная лаборатория Колорадский университет Университет Флориды
Докторант	Казимеж Куратовски
Докторанты	Пол Келли

Станислав Марцин Улам ([sta'ɲiswaf 'mart͡ɕin' ulam]; 3 апреля 1909 - 13 мая 1984) был польско-американским ученым в области математики и ядерной физики. Он участвовал в Манхэттенский проект, возникла Дизайн Теллера – Улама из термоядерное оружие открыл концепцию клеточный автомат, изобрел Метод вычисления Монте-Карло, и предложил ядерная импульсная тяга. В чистом виде и Прикладная математика, он доказал несколько теорем и выдвинул несколько гипотез.

Родился в богатой Польский еврей В семье Улам изучал математику в Львовский политехнический институт, где он заработал кандидат наук в 1933 г. под руководством Казимеж Куратовски. В 1935 г. Джон фон Нейман, которого Улам встретил в Варшаве, пригласил его приехать на Институт перспективных исследований в Принстон, Нью-Джерси, в течение нескольких месяцев. С 1936 по 1939 год он проводил лето в Польше и академические годы в Гарвардский университет в Кембридж, Массачусетс, где он работал над достижением важных результатов в отношении эргодическая теория. 20 августа 1939 года он в последний раз отплыл в Соединенные Штаты со своим 17-летним братом. Адам Улам. Он стал доцентом в Университет Висконсина-Мэдисона в 1940 г. и Гражданин США в 1941 г.

В октябре 1943 г. он получил приглашение от Ганс Бете присоединиться к Манхэттенский проект в секрете Лос-Аламосская лаборатория в Нью-Мексико. Там он работал над гидродинамический расчеты для прогнозирования поведения взрывные линзы которые были нужны оружие имплозивного типа. Он был назначен на Эдвард Теллер группа, в которой он работал "Супер" бомба Теллера для Теллера и Энрико Ферми. После войны он уехал, чтобы стать доцентом Университет Южной Калифорнии, но вернулся в Лос-Аламос в 1946 году для работы над термоядерное оружие. С помощью кадра женского пола "компьютеры ", включая его жену Франсуаза Арон Улам,^{[нужна цитата ]} он обнаружил, что «супер» дизайн Теллера не работает. В январе 1951 года Улам и Теллер придумали Дизайн Теллера – Улама, лежащая в основе всего термоядерного оружия.

Улам рассмотрел проблему ядерная двигательная установка ракет, которые преследовали Project Rover, и предложил в качестве альтернативы марсоходу ядерная тепловая ракета, чтобы использовать небольшие ядерные взрывы для движения, которое стало Проект Орион. С Ферми, Джон Паста, и Мэри Цинго, Улам изучил Проблема Ферми – Паста – Улама – Цингоу, который стал источником вдохновения для области нелинейной науки. Он, вероятно, известен прежде всего тем, что понял, что электронные компьютеры сделали практичным применение статистических методов к функциям без известных решений, и по мере развития компьютеров Метод Монте-Карло стал обычным и стандартным подходом ко многим проблемам.

Польша

Улам родился в Лемберг, Галиция 3 апреля 1909 г.^[1][2] В это время Галичина находилась в Королевство Галиции и Лодомерии из Австро-Венгерская империя, известный полякам как Австрийский раздел. В 1918 году он стал частью недавно восстановленной Польши, Вторая Польская Республика, и город снова получил свое польское название, Lwów.^[3]

Улемы были богатыми Польский еврей семья банкиров, промышленников и других профессионалов. Ближайшие родственники Улама были «обеспеченными, но вряд ли богатыми».^[4] Его отец, Юзеф Улам, родился во Львове и был юристом.^[3] и его мать Анна (урожденная Ауэрбах) родилась в Стрый.^[5] Его дядя, Михал Улам, был архитектором, строительным подрядчиком и лесопромышленником.^[6] С 1916 по 1918 год семья Юзефа временно жила в Вена.^[7] После их возвращения Львов стал эпицентром Польско-украинская война, во время которых город испытал украинская осада.^[3]

В Шотландское кафе в здании теперь находится Universal Bank в Львов, Украина.

В 1919 году Улам поступил в Львовскую гимназию Nr. VII, которую окончил в 1927 году.^[8] Затем он изучал математику в Львовском политехническом институте. под присмотром Казимеж Куратовски, он получил Магистр степень в 1932 году и стал Доктор наук в 1933 г.^[7][9] В 1929 году, когда ему было 20 лет, он опубликовал свою первую статью. О функции множеств в журнале Fundamenta Mathematicae.^[9] С 1931 по 1935 год он путешествовал и учился в Вильно (Вильнюс), Вена, Цюрих, Париж, и Кембридж, Англия, где он встретился Г. Х. Харди и Субраманян Чандрасекар.^[10]

Вместе с Станислав Мазур, Марк Кац, Влодзимеж Стожек, Куратовский и другие, Улам был членом Львовская математическая школа. Его основателями были Хьюго Штайнхаус и Стефан Банах, которые были профессорами в Университет Яна Казимежа. Математики этой «школы» подолгу встречались в Шотландское кафе, где обсуждаемые проблемы собраны в Шотландская книга, толстый блокнот, предоставленный женой Банаха. Улам был одним из основных авторов книги. Из 193 задач, записанных между 1935 и 1941 годами, он написал 40 задач как один автор, еще 11 с Банахом и Мазуром и еще 15 с другими. В 1957 году он получил от Штайнхауза экземпляр книги, пережившей войну, и перевел ее на английский язык.^[11] В 1981 году друг Улама Р. Дэниел Модлин опубликовал расширенную и аннотированную версию.^[12]

Приезд в США

В 1935 г. Джон фон Нейман, с которым Улам познакомился в Варшаве, пригласили его приехать на Институт перспективных исследований в Принстон, Нью-Джерси, в течение нескольких месяцев. В декабре того же года Улам отплыл в США. В Принстоне он ходил на лекции и семинары, где слышал Освальд Веблен, Джеймс Александр, и Альберт Эйнштейн. Во время чаепития в доме фон Неймана он встретил Г. Д. Биркгоф, который предложил ему подать заявку на должность с Гарвардское общество стипендиатов.^[7] Следуя предложению Биркгофа, Улам провел лето в Польше, а академические годы в Гарвардский университет в Кембридж, Массачусетс с 1936 по 1939 год, где работал с Джон К. Окстоби установить результаты в отношении эргодическая теория. Они появились в Анналы математики в 1941 г.^[8][13]

20 августа 1939 г. в г. Гдыня Юзеф Улам вместе со своим братом Шимоном поставил двух своих сыновей, Станислава и 17-летнего Адам, на корабле, направляющемся в США.^[7] Одиннадцать дней спустя Немцы вторглись в Польшу. В течение двух месяцев немцы завершили свой Занятие Западной Польши и Советы вторгся и оккупировал восточную Польшу. В течение двух лет Юзеф Улам и остальные члены его семьи стали жертвами Холокост, Хьюго Штайнхаус скрывался, Казимеж Куратовски читал лекции в подпольный университет в Варшаве, Влодзимеж Стожек и два его сына были убиты в резня львовских профессоров, а последняя проблема была записана в Шотландская книга. Стефан Банах пережил нацистскую оккупацию, накормив вши в Исследовательский институт тифа Рудольфа Вайгля. В 1963 г. Адам Улам, который стал выдающимся кремленолог в Гарварде,^[14] получил письмо от Георгия Вольского,^[15] который спрятался в доме Юзефа Улама после дезертирства из польской армии. Это воспоминание дает пугающий отчет о хаотических сценах Львова в конце 1939 года.^[16] В более поздней жизни Улам называл себя «агностиком. Иногда я глубоко размышляю о силах, которые для меня невидимы. Когда я почти приближаюсь к идее Бога, я сразу чувствую себя отчужденным ужасами этого мира, которые он, кажется, терпеть ".^[17]

В 1940 году по рекомендации Биркгофа Улам стал доцентом Университет Висконсина-Мэдисона. Здесь он стал Гражданин США в 1941 г.^[7] В том году он женился Франсуаза Арон.^[8] Она училась по французскому обмену в Колледж Mount Holyoke, которого он встретил в Кембридже. У них родилась дочь Клэр. В Мэдисоне Улам познакомился со своим другом и коллегой К. Дж. Эвереттом, с которым он сотрудничал с рядом статей.^[18]

Манхэттенский проект

Фотография на пропуск Улама из Лос-Аламос

В начале 1943 года Улам попросил фон Неймана найти ему военную работу. В октябре он получил приглашение присоединиться к неизвестному проекту недалеко от г. Санта-Фе, Нью-Мексико.^[7] Письмо подписал Ганс Бете, который был назначен руководителем теоретического отдела Лос-Аламосская национальная лаборатория от Роберт Оппенгеймер, его научный руководитель.^[19] Ничего не зная об этом районе, он позаимствовал путеводитель по Нью-Мексико. На карточке кассы он нашел имена своих коллег из Висконсина, Джоан Хинтон, Дэвид Фриш, и Джозеф Маккиббен, все они загадочным образом исчезли.^[7] Это было введение Улама в Манхэттенский проект, который был попыткой США создать атомную бомбу во время войны.^[20]

Гидродинамические расчеты имплозии

Через несколько недель после того, как Улам достиг Лос-Аламос в феврале 1944 года проект пережил кризис. В апреле, Эмилио Сегре обнаружил, что плутоний сделано в реакторы не будет работать в пушечный плутониевое оружие, подобное "Тонкий человек ", который разрабатывался параллельно с урановым оружием,"Маленький мальчик "что было сброшено на Хиросима. Эта проблема грозила потратить впустую огромные инвестиции в новые реакторы на заводе. Хэнфордский сайт и сделать медленным разделение изотопов урана единственный способ подготовиться делящийся материал, пригодный для использования в бомбах. Чтобы отреагировать на это, Оппенгеймер в августе осуществил радикальную реорганизацию лаборатории, чтобы сосредоточиться на разработке оружие имплозивного типа и назначил Георгий Кистяковский начальник отдела имплозии. Он был профессором Гарварда и специалистом по точному использованию взрывчатых веществ.^[21]

Основная концепция взрыв состоит в том, чтобы использовать химические взрывчатые вещества, чтобы раздробить кусок делящегося материала в критическая масса, где нейтрон умножение приводит к ядерная цепная реакция, высвобождая большое количество энергии. Цилиндрические имплозивные конфигурации были изучены Сет Неддермейер, но фон Нейман, имевший опыт работы с кумулятивные заряды используется в бронебойные боеприпасы, был вокальный сторонник сферической имплозии обусловлен взрывные линзы. Он понял, что симметрия и скорость, с которой имплозия сжимает плутоний, имеют решающее значение.^[21] и привлек Улама для помощи в разработке конфигураций линз, обеспечивающих почти сферическое сжатие. Во время имплозии из-за огромного давления и высоких температур твердые материалы ведут себя так же, как жидкости. Это означало, что гидродинамический расчеты были необходимы, чтобы предсказать и минимизировать асимметрии, которые могут испортить ядерный взрыв. Об этих расчетах Улам сказал:

Задача гидродинамики была просто сформулирована, но ее очень трудно вычислить - не только в деталях, но даже по порядку величины. В этом обсуждении я подчеркнул чистый прагматизм и необходимость получить эвристический обзор проблемы с помощью простой грубой силы, а не массивной численной работы.^[7]

Тем не менее, с примитивными средствами, доступными в то время, Улам и фон Нейман действительно выполнили численные вычисления, которые привели к удовлетворительному проекту. Это мотивировало их отстаивание мощных вычислительных возможностей в Лос-Аламосе, начатое в годы войны.^[22] продолжалась во времена «холодной войны» и существует до сих пор.^[23] Отто Фриш Вспомнил Улама как «блестящего польского тополога с очаровательной французской женой. Он сразу сказал мне, что он чистый математик, который опустился так низко, что его последняя статья фактически содержала числа с десятичной точкой!»^[24]

Статистика ветвящихся и мультипликативных процессов

Даже собственные статистические колебания нейтрон умножение в цепная реакция имеют значение в отношении скорости и симметрии имплозии. В ноябре 1944 г. Дэвид Хокинс^[25] и Улам рассмотрел эту проблему в докладе, озаглавленном «Теория мультипликативных процессов».^[26] Этот отчет, который вызывает функции, генерирующие вероятность, также одна из первых статей в обширной литературе по статистике разветвление и мультипликативные процессы. В 1948 году его возможности расширили Улам и Эверетт.^[27]

В начале манхэттенского проекта Энрико Ферми Внимание было сосредоточено на использовании реакторов для производства плутония. В сентябре 1944 года он прибыл в Лос-Аламос, вскоре после того, как вдохнул жизнь в первый реактор в Хэнфорде, который был отравлен по изотоп ксенона.^[28] Вскоре после прибытия Ферми "Супер" бомба Теллера Группа, в которую входил Улам, была переведена в новое подразделение, возглавляемое Ферми.^[29] Между Ферми и Уламом сложились отношения, которые после войны стали очень плодотворными.^[30]

Послевоенный Лос-Аламос

В сентябре 1945 года Улам покинул Лос-Аламос, чтобы стать адъюнкт-профессором в Университет Южной Калифорнии в Лос-Анджелес. В январе 1946 года у него случился острый приступ. энцефалит, что подвергло его жизнь опасности, но было облегчено после экстренной операции на головном мозге. Во время его выздоровления его посетили многие друзья, в том числе Николай Метрополис из Лос-Аламоса и знаменитый математик Пол Эрдёш,^[31] который заметил: «Стэн, ты такой же, как раньше».^[7] Это обнадежило, потому что Улама беспокоило состояние своих умственных способностей, так как он потерял способность говорить во время кризиса. Другой друг, Джан-Карло Рота, утверждал в статье 1987 года, что это нападение изменило личность Улама: впоследствии он перешел от строгой чистой математики к более умозрительным предположениям относительно применения математики к физике и биология; Рота также цитирует бывшего сотрудника Улама Пола Штейна, который отметил, что Улам впоследствии был более небрежен в своей одежде, и Джона Окстоби, отметившего, что Улам до энцефалита мог часами работать, выполняя вычисления, в то время как, когда Рота работал с ним, неохотно решал даже квадратное уравнение.^[32] Это утверждение не было принято Франсуаза Арон Улам.^[33]

К концу апреля 1946 года Улам достаточно поправился, чтобы присутствовать на секретной конференции в Лос-Аламосе, чтобы обсудить термоядерное оружие. Присутствовали Улам, фон Нейман, Метрополис, Теллер, Стэн Франкель, и другие. На протяжении всего своего участия в Манхэттенском проекте усилия Теллера были направлены на разработку «супероружия» на основе термоядерная реакция, а не к разработке практической бомбы деления. После обстоятельного обсуждения участники пришли к единому мнению, что его идеи достойны дальнейшего изучения. Несколько недель спустя Улам получил предложение о работе в Лос-Аламосе от Метрополиса и Роберт Д. Рихтмайер, новый руководитель его теоретического отдела с более высокой зарплатой, и улам вернулся в Лос-Аламос.^[34]

Метод Монте-Карло

Стэн Улам держит ФЕРМИАК

В конце войны, при спонсорской поддержке фон Неймана, Франкель и Метрополис начали проводить расчеты на первом электронном компьютере общего назначения, ENIAC на Абердинском полигоне в Мэриленде. Вскоре после возвращения в Лос-Аламос Улам принял участие в обзоре результатов этих расчетов.^[35] Раньше во время игры пасьянс Во время выздоровления после операции Улам думал о том, чтобы сыграть в сотни игр, чтобы статистически оценить вероятность успешного исхода.^[36] Помня об ENIAC, он понял, что доступность компьютеров делает такие статистические методы очень практичными. Джон фон Нейман сразу понял значение этого открытия. В марте 1947 года он предложил статистический подход к проблеме диффузии нейтронов в делящемся материале.^[37] Поскольку Улам часто упоминал своего дядю, Михала Улама, «которому просто нужно было поехать в Монте-Карло», чтобы играть в азартные игры, Метрополис назвал статистический подход « Метод Монте-Карло ".^[35] Метрополис и Улам опубликовали первую несекретную статью о методе Монте-Карло в 1949 году.^[38]

Ферми, узнав о прорыве Улама, разработал аналоговый компьютер известный как Тележка Монте-Карло, позже названный ФЕРМИАК. Устройство выполнило механическое моделирование случайной диффузии нейтронов. По мере того, как компьютеры становились более быстрыми и программируемыми, эти методы стали более полезными. В частности, многие расчеты Монте-Карло, выполненные на современных массивно параллельный суперкомпьютеры находятся смущающе параллельный приложения, результаты которых могут быть очень точными.^[23]

Дизайн Теллера – Улама

29 августа 1949 г. Советский Союз испытал свою первую бомбу деления, РДС-1. Создано под руководством Лаврентий Берия, который стремился дублировать усилия США, это оружие было почти идентично Толстяк, поскольку его конструкция была основана на информации, предоставленной шпионами Клаус Фукс, Теодор Холл, и Дэвид Грингласс. В ответ 31 января 1950 г. Президент Гарри С. Трумэн объявил о краш-программе по разработке термоядерной бомбы.^[39]

Чтобы отстаивать агрессивную программу развития, Эрнест Лоуренс и Луис Альварес приехали в Лос-Аламос, где они совещались с Норрис Брэдбери, заведующий лабораторией, и с Георгий Гамов, Эдвард Теллер, и Улам. Вскоре эти трое стали членами недолговечного комитета, назначенного Брэдбери для изучения проблемы с Теллером в качестве председателя.^[7] В настоящее время проводятся исследования по использованию оружия деления для создания реакция синтеза разрабатывался с 1942 года, но конструкция по-прежнему оставалась той, которая была предложена Теллером. Его концепция заключалась в том, чтобы поставить тритий и / или дейтерий в непосредственной близости от бомбы деления, в надежде, что тепло и интенсивный поток нейтронов, выпущенных при взрыве бомбы, воспламенит самоподдерживающийся реакция синтеза. Реакции этих изотопы водорода представляют интерес, потому что энергия на единицу массы топлива, выделяемая при их синтезе, намного больше, чем при делении тяжелых ядер.^[40]

Айви Майк, первая полная проверка дизайна Теллера – Улама ( постановочный термоядерная бомба), с Уступать 10,4 мегатонн на 1 ноября 1952 г.

Поскольку результаты расчетов, основанных на концепции Теллера, обескураживали, многие ученые считали это не мог привести к успешному оружию, в то время как у других были моральные и экономические основания для отказа. Следовательно, против развития выступили несколько высокопоставленных лиц Манхэттенского проекта, в том числе Бете и Оппенгеймер.^[41] Чтобы прояснить ситуацию, Улам и фон Нейман решили провести новые расчеты, чтобы определить, осуществим ли подход Теллера. Для проведения этих исследований фон Нейман решил использовать электронные компьютеры: ENIAC в Абердине, новый компьютер, МАНЬЯК, в Принстоне, и его близнец, который строился в Лос-Аламосе. Улам заручился поддержкой Эверетта, чтобы тот последовал совершенно иному подходу, основанному на физической интуиции. Франсуаза Улам был одним из^{[нужна цитата ]} кадры женщин "компьютеры "кто выполнил кропотливые и обширные вычисления термоядерных сценариев на механические калькуляторы, дополненный и подтвержденный Эвереттом логарифмическая линейка. Улам и Ферми совместно работали над дальнейшим анализом этих сценариев. Результаты показали, что в рабочих конфигурациях термоядерная реакция не будет воспламеняться, а в случае воспламенения она не будет самоподдерживающейся. Улам использовал свой опыт в комбинаторика чтобы проанализировать цепную реакцию в дейтерии, которая была намного сложнее, чем в уране и плутонии, и он пришел к выводу, что самоподдерживающаяся цепная реакция не будет происходить при (низких) плотностях, которые рассматривал Теллер.^[42] В конце 1950 г. эти выводы были подтверждены результатами фон Неймана.^[33][43]

В январе 1951 года Улама возникла другая идея: направить механический удар ядерного взрыва так, чтобы сжать термоядерное топливо. По рекомендации жены,^[33] Улам обсудил эту идею с Брэдбери и Марком, прежде чем рассказал об этом Теллеру.^[44] Практически сразу Теллер увидел его достоинства, но заметил, что мягкий Рентгеновские лучи бомба деления сжимала бы термоядерное топливо сильнее, чем механический удар, и предлагал способы усилить этот эффект. 9 марта 1951 года Теллер и Улам представили совместный отчет с описанием этих нововведений.^[45] Несколько недель спустя Теллер предложил разместить делящийся стержень или цилиндр в центре термоядерного топлива. Детонация этой «свечи зажигания»^[46] поможет инициировать и усилить реакцию синтеза. Конструкция, основанная на этих идеях, названная ступенчатой ​​радиационной имплозией, стала стандартным способом создания термоядерного оружия. Его часто называют "Дизайн Теллера – Улама ".^[47]

В Колбаса устройство Майк ядерное испытание (мощность 10,4 Мт) на Атолл Эниветак. Тест был частью Операция Плющ. Колбаса была первой испытанной настоящей водородной бомбой, то есть первой термоядерный устройство построено на Теллер-Улам принципы ступенчатой ​​радиационной имплозии.

В сентябре 1951 года, после ряда разногласий с Брэдбери и другими учеными, Теллер ушел из Лос-Аламоса и вернулся в Чикагский университет.^[48] Примерно в то же время Улам ушел в отпуск на семестр в качестве приглашенного профессора в Гарвард.^[49] Хотя Теллер и Улам представили совместный отчет о своем дизайне^[45] и совместно подали заявку на патент на него,^[20] вскоре они оказались вовлечены в спор о том, кто заслуживает уважения.^[44] После войны Бете вернулся в Корнелл Университет, но он был глубоко вовлечен в разработку термоядерного оружия в качестве консультанта. В 1954 году он написал статью об истории водородной бомбы.^[50] который представляет его мнение, что оба мужчины внесли очень значительный вклад в прорыв. Это уравновешенное мнение разделяют и другие участники, в том числе Марк и Ферми, но Теллер настойчиво пытался преуменьшить роль Улама.^[51] «После того, как была изготовлена ​​водородная бомба, - вспоминал Бете, - репортеры стали называть Теллера отцом водородной бомбы. Ради истории, я думаю, было бы более точно сказать, что Улам - отец, потому что он предоставил семя, а Теллер - мать, потому что он остался с ребенком. Что касается меня, полагаю, я акушерка ».^[52]

Когда основные реакции синтеза были подтверждены, и при наличии осуществимой конструкции ничто не могло помешать Лос-Аламосу испытать термоядерное устройство. 1 ноября 1952 г. произошел первый термоядерный взрыв, когда Айви Майк был взорван на Атолл Эниветак, в США Тихоокеанский полигон. Это устройство, в котором в качестве термоядерного топлива использовался жидкий дейтерий, было огромным и совершенно непригодным для использования в качестве оружия. Тем не менее, его успех подтвердил проект Теллера – Улама и стимулировал интенсивную разработку практического оружия.^[49]

Проблема Ферми – Паста – Улама – Цингоу

Основная статья: Проблема Ферми – Паста – Улама – Цингоу

Когда Улам вернулся в Лос-Аламос, его внимание переключилось с дизайна оружия на использование компьютеров для исследования проблем физики и математики. С участием Джон Паста, который помог Метрополису ввести MANIAC в действие в марте 1952 года, он исследовал эти идеи в отчете «Эвристические исследования проблем математической физики на высокоскоростных вычислительных машинах», который был представлен 9 июня 1953 года. В нем рассмотрены несколько проблем, которые невозможно решить. рассматриваются в рамках традиционных аналитических методов: вспучивание жидкостей, вращательное движение в гравитирующих системах, магнитные силовые линии и гидродинамические неустойчивости.^[53]

Вскоре Паста и Улам приобрели опыт работы с электронными вычислениями на МАНИАКе, и к этому времени Энрико Ферми привык проводить академические годы в Чикагском университете, а летом - в Лос-Аламосе. Во время этих летних визитов Паста, Улам и Мэри Цинго, программист из группы MANIAC, присоединился к нему, чтобы изучить вариант классической задачи о цепочке масс, удерживаемых вместе пружинами, которые создают силы, линейно пропорциональные их смещению из состояния равновесия.^[54] Ферми предложил добавить к этой силе нелинейную составляющую, которая может быть выбрана пропорциональной квадрату или кубу смещения или более сложной «ломаной линейной» функции. Это дополнение является ключевым элементом Проблема Ферми – Паста – Улама – Цингоу, который часто обозначается аббревиатурой FPUT.^[55][56]

Классическую пружинную систему можно описать с помощью форм колебаний, которые аналогичны гармоникам, возникающим на натянутой струне скрипки. Если система запускается в одном режиме, вибрации в других режимах не развиваются. Что касается нелинейной составляющей, Ферми ожидал, что энергия в одной моде будет постепенно переходить в другие моды и, в конечном итоге, будет равномерно распределена между всеми модами. Это примерно то, что начало происходить вскоре после того, как система была инициализирована со всей своей энергией в самом низком режиме, но намного позже по существу вся энергия периодически появлялась в низшем режиме.^[56] Такое поведение сильно отличается от ожидаемого. равнораспределение энергии. Это оставалось загадкой до 1965 года, когда Крускал и Забуский показал, что после соответствующих математических преобразований система может быть описана Уравнение Кортевега – де Фриза, который является прототипом нелинейного уравнения в частных производных который имеет солитон решения. Это означает, что поведение FPUT можно понять в терминах солитонов.^[57]

Ядерная двигательная установка

Художественная концепция эталонного дизайна НАСА для космического корабля проекта Орион с ядерной силовой установкой.

Начиная с 1955 г., Улам и Фредерик Райнес считается ядерная двигательная установка самолетов и ракет.^[58] Это привлекательная возможность, потому что ядерная энергия на единицу массы топлива в миллион раз больше, чем энергия, получаемая от химикатов. С 1955 по 1972 год их идеи воплощались в жизнь. Project Rover, который исследовал использование ядерных реакторов для запуска ракет.^[59] В ответ на вопрос сенатора Джон О. Пасторе 22 января 1958 года на слушаниях комитета Конгресса по теме «Приведение в движение космического пространства с помощью ядерной энергии» Улам ответил, что «будущее всего человечества сейчас в некоторой степени неотвратимо связано с выходом за пределы земного шара».^[60]

Улам и К. Дж. Эверетт также предложили, в отличие от Непрерывный нагрев выхлопа ракеты марсоходом, чтобы использовать небольшие ядерные взрывы для движения.^[61] Проект Орион было исследование этой идеи. Он начался в 1958 году и закончился в 1965 году, после Договор о частичном запрещении ядерных испытаний 1963 г. запрещены испытания ядерного оружия в атмосфере и в космосе.^[62] Работу над этим проектом возглавил физик. Фриман Дайсон, который прокомментировал решение о закрытии Orion в своей статье «Смерть проекта».^[63]

Брэдбери назначил Улама и Джон Х. Мэнли в качестве советников по исследованиям директора лаборатории в 1957 г. Эти вновь созданные должности находились на том же административном уровне, что и руководители подразделений, и Улам занимал свои должности до тех пор, пока не ушел на пенсию из Лос-Аламоса. В этом качестве он мог влиять и направлять программы во многих разделах: теоретические, физика, химия, металлургия, оружие, здоровье, вездеход и другие.^[59]

В дополнение к этой деятельности Улам продолжал публиковать технические отчеты и исследовательские работы. Один из них представил Модель Ферми – Улама, расширение теории Ферми ускорение космических лучей.^[64] Другой, с Полем Штайном и Мэри Цинго под названием "Квадратичные преобразования" было ранним исследованием теория хаоса и считается первым опубликованным использованием фразы "хаотичное поведение ".^[65][66]

Вернуться в академию

Когда положительные целые числа расположены вдоль Спираль Улама, простые числа, представленные точками, обычно собираются вдоль диагональных линий.

Во время своего пребывания в Лос-Аламосе Улам был приглашенным профессором в Гарварде с 1951 по 1952 год. Массачусетский технологический институт с 1956 по 1957 г. Калифорнийский университет в Сан-Диего, в 1963 г., а Колорадский университет в Боулдере с 1961 по 1962 год и с 1965 по 1967 год. В 1967 году последняя из этих должностей стала постоянной, когда Улам был назначен профессором и заведующим кафедрой математики в Боулдер, Колорадо. Он жил в Санта-Фе, Нью-Мексико, благодаря чему было удобно проводить лето в Лос-Аламосе в качестве консультанта.^[67]

В Колорадо, где он воссоединился со своими друзьями Гамовым, Рихтмайером и Хокинсом, исследовательские интересы Улама повернулись к биология. В 1968 г., осознавая этот акцент, Медицинский факультет Университета Колорадо назначил Улама профессором биоматематики, и он занимал эту должность до своей смерти. Вместе со своим коллегой из Лос-Аламоса Робертом Шрандтом он опубликовал отчет «Некоторые элементарные попытки численного моделирования проблем, касающихся темпов эволюционных процессов», в котором применял его более ранние идеи о ветвящихся процессах к биологической наследственности.^[68] Другой, отчет с Уильямом Бейером, Темпл Ф. Смит и М. Л. Штейн, озаглавленный «Метрики в биологии», представили новые идеи о биометрических расстояниях.^[69]

Когда он вышел на пенсию из Колорадо в 1975 году, Улам начал проводить зимние семестры в Университет Флориды, где он был дипломированным профессором-исследователем. Кроме творческий отпуск на Калифорнийский университет в Дэвисе с 1982 по 1983 год, а в Рокфеллеровский университет с 1980 по 1984 г.,^[67] такая схема проведения лета в Колорадо и Лос-Аламосе и зимы во Флориде продолжалась до тех пор, пока Улам не умер от сердечного приступа в Санта-Фе 13 мая 1984 года.^[2]Пол Эрдёш отметил, что «он умер внезапно от сердечной недостаточности, без страха и боли, хотя он еще мог доказывать и предполагать».^[31] В 1987 г. Франсуаза Улам сдал свои бумаги в Американское философское общество Библиотека в Филадельфия.^[70] Она продолжала жить в Санта-Фе, пока не умерла 30 апреля 2011 года в возрасте 93 лет. Франсуаза и ее муж похоронены вместе со своей французской семьей в Кладбище Монпарнас в Париже.^[71][72]

Вызов экономике

Альфред Маршалл и его ученики доминировали в экономической теории до конца Второй мировой войны. С началом холодной войны теория изменилась, подчеркнув, что рыночная экономика является более совершенной и единственно разумной. В Пол Самуэльсон В «Экономике: вводный анализ», 1948 г., «невидимая рука» Адама Смита была лишь сноской. В более поздних изданиях это стало центральной темой.

Как Самуэльсон ^[73] вспоминает, все это было оспорено Станиславом Уламом: «[Y] несколько лет назад ... Я был членом Общества стипендиатов в Гарварде вместе с математиком Станиславом Уламом. Улам, который должен был стать создателем метода Монте-Карло и его коллегами. - открыватель водородной бомбы, ... дразнил меня, говоря: «Назовите мне одно утверждение во всех социальных науках, которое одновременно истинно и нетривиально». Это был тест, который я всегда терпел неудачно. Но теперь, спустя тридцать лет ... мне приходит в голову подходящий ответ: Рикардианский теория сравнительное преимущество .... То, что это логически верно, не нужно доказывать перед математиком; то, что это нетривиально, подтверждают тысячи важных и умных людей, которые никогда не были способны понять это учение для себя или поверить в него после того, как оно им было объяснено ".

Влияние и наследие

С момента публикации своей первой студенческой работы в 1929 году до своей смерти Улам постоянно писал по математике. Список публикаций Улама включает более 150 статей.^[8] Темы, представленные значительным количеством статей: теория множеств (в том числе измеримые кардиналы и абстрактные меры ), топология, теория трансформации, эргодическая теория, теория групп, проективная алгебра, теория чисел, комбинаторика, и теория графов.^[74] В марте 2009 г. Математические обзоры В базе данных 697 статей с наименованием «Улам».^[75]

Заметными результатами этой работы являются:

Теорема Борсука – Улама. Теорема Мазура – ​​Улама Теорема Куратовского – Улама Стабильность Хайерса – Улама – Рассиаса Счастливый номер Спираль Улама

Гипотеза Улама (в теории чисел) Гипотеза Улама (в теории графов) Гипотеза Улама об упаковке Игра Улама Матрица Улама Номера улама

Станислав Улам, сыгравший ключевую роль в разработке термоядерного оружия, изменил мир. По словам Франсуазы Улам: «Стэн заверил бы меня, что, исключая несчастные случаи, водородная бомба делает ядерную войну невозможной».^[33] В 1980 году Улам с женой снялись в документальном телефильме. День после Троицы.^[76]

Анимация, демонстрирующая решето счастливых чисел. Цифры в красном - счастливые числа

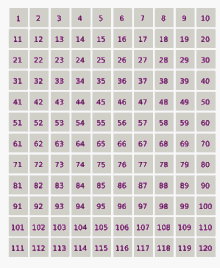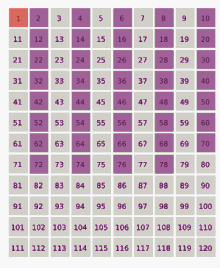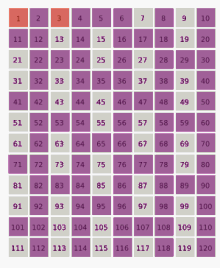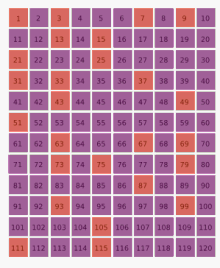
В Метод Монте-Карло стал повсеместным и стандартным подходом к вычислениям, и этот метод был применен к огромному количеству научных проблем.^[77] Помимо задач по физике и математике, метод был применен к финансы, социальная наука,^[78] экологический оценка рисков,^[79] лингвистика^[80] радиационная терапия,^[81] и спорт.^[82]

В Проблема Ферми – Паста – Улама – Цингоу считается не только «рождением экспериментальной математики»,^[56] но также как источник вдохновения для обширной области нелинейной науки. В его Премия Лилиенфельда лекция Дэвид К. Кэмпбелл отметил эту взаимосвязь и описал, как FPUT породил идеи в хаос, солитоны, и динамические системы.^[83] В 1980 г. Дональд Керр, директор лаборатории в Лос-Аламосе при сильной поддержке Улама и Марк Кац,^[84] основал Центр нелинейных исследований (CNLS).^[85] В 1985 году CNLS инициировал Станислав М. Улам заслуженный ученый Программа, которая предусматривает ежегодную награду, позволяющую известному ученому провести год, проводя исследования в Лос-Аламосе.^[86]

Пятидесятилетие оригинальной статьи FPUT стало темой мартовского номера журнала Chaos за 2005 год.^[87] и тема 25-й ежегодной международной конференции CNLS.^[88] В Университет Южного Миссисипи и Университет Флориды поддержал Ulam Quarterly,^[89] который был активен с 1992 по 1996 год и был одним из первых математических онлайн-журналов.^[90] Департамент математики Флориды с 1998 г. спонсирует ежегодный Лекция коллоквиума Улама,^[91] а в марте 2009 г. Конференция столетия Улама.^[92]

Работа Улама по не-Метрики евклидова расстояния в контексте молекулярной биологии внесла значительный вклад в анализ последовательности^[93] и его вклад в теоретическую биологию считается водоразделом в развитии клеточные автоматы теория^[94][95] популяционная биология, распознавание образов и биометрия в целом (Дэвид Санкофф, однако, оспорил выводы Уолтера, написав, что Улам имел лишь умеренное влияние на раннюю разработку методов выравнивания последовательностей.^[96]). Коллеги отметили, что одним из самых больших его вкладов было четкое определение проблем, которые необходимо решить, и общих методов их решения.^[97]

В 1987 году Лос-Аламос выпустил специальный выпуск своей Наука публикация, в которой обобщены его достижения,^[98] и вышедшая в 1989 г. как книга От кардиналов к хаосу. Точно так же в 1990 году Калифорнийский университет Press опубликовал сборник математических отчетов Улама и его сотрудников из Лос-Аламоса: Аналогии между аналогиями.^[99] За свою карьеру Улам был удостоен почетных степеней университетов Нью-Мексико, Висконсин, и Питтсбург.^[7]

Список используемой литературы

• Кац, Марк; Улам, Станислав (1968). Математика и логика: взгляд в прошлое и перспективы. Нью-Йорк: Praeger. ISBN  978-0-486-67085-0. OCLC  24847821.
• Улам, Станислав (1974). Beyer, W. A .; Mycielski and, J .; Рота, Г.-К. (ред.). Наборы, числа и вселенные: избранные произведения. Математики нашего времени. 9. MIT Press, Кембридж, Массачусетс - Лондон. ISBN  978-0-262-02108-1. Г-Н  0441664.
• Улам, Станислав (1960). Сборник математических задач. Нью-Йорк: Interscience Publishers. OCLC  526673.
• Улам, Станислав (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. ISBN  978-0-684-14391-0. OCLC  1528346. (автобиография).
• Улам, Станислав (1986). Наука, компьютеры и люди: от древа математики. Бостон: Биркхаузер. ISBN  978-3-7643-3276-1. OCLC  11260216.
• Улам, Станислав; Улам, Франсуаза (1990). Аналогии между аналогиями: Математические отчеты С.М. Улам и его сотрудники из Лос-Аламоса. Беркли: Калифорнийский университет Press. ISBN  978-0-520-05290-1. OCLC  20318499.

Смотрите также

• Список вещей, названных в честь Станислава Улама
• Биографический фильм о Станиславе Улама, основанный на его автобиографии, в главной роли Якуб Гиршаль^[100]

использованная литература

1. Чартран, Гэри; Чжан, Пин (20 мая 2013 г.). Первый курс теории графов. Курьерская корпорация. п. 78. ISBN  978-0-486-29730-9.
2. Салливан, Уолтер (15 мая 1984 г.). "Станислав Улам, теоретик водородной бомбы". Газета "Нью-Йорк Таймс. Получено 30 мая 2013.
3. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.9–15. ISBN  9780684143910. OCLC  1528346.
4. Улам, Адам Бруно (2002). Понимание холодной войны: личные размышления историка. Нью-Брансуик, Нью-Джерси: Издатели транзакций. п. 19. ISBN  9780765808851. OCLC  48122759. Получено 28 декабря 2011.
5. Улам, Молли (25 июня 2000 г.). "Семья Улам из Львова; Ауэрбахи из Вены". Genforum. Получено 10 октября 2011.
6. «Генеалогия Михаила Улама». GENi. 24 мая 2011. Получено 12 октября 2011.
7. Улам, Франсуаза (1987). "Vita: выдержки из Приключения математика" (PDF). Лос-Аламосская национальная лаборатория. Архивировано из оригинал (PDF) 14 января 2009 г.. Получено 7 октября 2011.
8. Цесельский, Крыжистоф; Термистокл Рассиас (2009). «О Стэне Улама и его математике» (PDF). Австралийский журнал математического анализа и приложений. Получено 10 октября 2011. v 6, nr 1, pp 1-9, 2009
9. Анджей М. Кобос (1999). "Mędrzec większy niż życie" [Мудрец выше жизни]. Zwoje (по польски). 3 (16). Получено 10 мая 2013.
10. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.56–60. ISBN  9780684143910. OCLC  1528346.
11. Улам, Станислав (ноябрь 2002 г.). "Предисловие к" шотландской книге"". WWW сервер Turnbull. Школа математических и вычислительных наук Университета Сент-Эндрюс. Получено 11 сентября 2012.
12. Модлин, Р. Дэниел (1981). Шотландская книга. Бирхаузер. п. 268. ISBN  9783764330453. OCLC  7553633. Получено 4 декабря 2011.
13. "Некролог Джона К., Окстоби". Нью-Йорк Таймс. 5 января 1991 г.. Получено 10 октября 2011.
14. «Некролог Адаму Улама». Вестник Гарвардского университета. 6 апреля 2000 г.. Получено 10 октября 2011.
15. Вольский, Георгий (23 декабря 1963 г.). "Письмо о Юзефе Уламе". С тревогой из Львова. Адам Улам. Архивировано из оригинал 17 мая 2013 г.. Получено 24 мая 2013.
16. "Lwow живет в Леополис Пресс". Крюк. 14 ноября 2002 г.. Получено 10 октября 2011.
17. Будревич /, Ольгерд (1977). Новый взгляд на плавильный котел: двадцать известных пользователей польского происхождения. Интерпресс. п. 36. Получено 11 сентября 2012.
18. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.125–130, 174. ISBN  9780684143910. OCLC  1528346.
19. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.143–147. ISBN  9780684143910. OCLC  1528346.
20. "Персональная биография Станислава Улама". Лос-Аламосская национальная лаборатория. Получено 22 октября 2011.
21. Ходдсон, Лилиан; Хенриксен, Пол В .; Мид, Роджер А .; Вестфол, Кэтрин Л. (1993). Критическая сборка: техническая история Лос-Аламоса в годы Оппенгеймера, 1943–1945 гг.. Нью-Йорк: Издательство Кембриджского университета. стр.130–137. ISBN  978-0-521-44132-2. OCLC  26764320.
22. «Суперкомпьютеры». История @ Лос-Аламос. Лос-Аламосская национальная лаборатория. Получено 24 октября 2011.
23. «От калькуляторов к компьютерам». История @ Лос-Аламос. Лос-Аламосская национальная лаборатория. Получено 24 октября 2011.
24. Фриш, Отто (Апрель 1974 г.). "Кто-то включил солнце выключателем". Бюллетень ученых-атомщиков. 30 (4): 17. Bibcode:1974BuAtS..30d..12F. Дои:10.1080/00963402.1974.11458102. Получено 29 мая, 2013.
25. Леманн, Кристофер (4 марта 2002 г.). "Некролог Дэвида Хокинса". Нью-Йорк Таймс. Получено 14 октября 2011.
26. Hawkins, D .; С. Улам (14 ноября 1944 г.). «Теория мультипликативных процессов» (PDF). Отчет LANL LA-171. Получено 13 октября 2011.
27. Ulam, S .; Эверетт, К. Дж. (7 июня 1948 г.). «Мультипликативные системы нескольких переменных I, II, III». Отчеты LANL. Калифорнийский университет Press. Получено 13 октября 2011.
28. Хьюлетт, Ричард Г.; Андерсон, Оскар Э. (1962). Новый мир, 1939–1946 гг. (PDF). Университетский парк: издательство Пенсильванского государственного университета. С. 304–307. ISBN  978-0-520-07186-5. OCLC  637004643.
29. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.152–153. ISBN  9780684143910. OCLC  1528346.
30. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.162–157. ISBN  9780684143910. OCLC  1528346.
31. Эрдош, Пол (1985). «Улам, человек и математик» (PDF). J. Теория графов, т. 9, стр. 445-449.. Получено 10 октября 2011.
32. Рота, Джан-Карло. "Стэн Улам: Затерянное кафе" (PDF). Лос-Аламосская наука, № 15, 1987 г.. Получено 22 октября 2011.
33. Улам, Франсуаза (1991). Постскриптум к приключениям математика. Беркли, Калифорния: Калифорнийский университет. ISBN  978-0-520-07154-4.
34. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.184–187. ISBN  9780684143910. OCLC  1528346.
35. Метрополис, Николай (1987). «Начало метода Монте-Карло» (PDF). Лос-Аламос Сайенс, № 15. Получено 22 октября 2011.
36. Экхардт, Роджер (1987). «Стэн Улам, Джон фон Нейман и метод Монте-Карло» (PDF). Лос-Аламос Сайенс, № 15. Получено 22 октября 2011.
37. Richtmyer, D .; J. Pasta; С. Улам (9 апреля 1947 г.). «Статистические методы диффузии нейтронов» (PDF). Отчет LANL LAMS-551. Получено 23 октября 2011.
38. Метрополис, Николай; Станислав Улам (1949). «Метод Монте-Карло» (PDF). Журнал Американской статистической ассоциации. 44 (247): 335–341. Дои:10.1080/01621459.1949.10483310. JSTOR  2280232. PMID  18139350. Получено 21 ноября 2011.
39. Хьюлетт, Ричард Г.; Дункан, Фрэнсис (1969). Атомный щит, том II, 1947–1952 гг.. История Комиссии по атомной энергии США. Университетский парк, Пенсильвания: Издательство Пенсильванского государственного университета. С. 406–409. ISBN  978-0-520-07187-2.
40. Родос, Ричард (1995). Темное Солнце: Создание водородной бомбы. Нью-Йорк: Саймон и Шустер. п.248. ISBN  978-0-684-80400-2.
41. Хьюлетт, Ричард Дж .; Дункан, Фрэнсис (1969). Атомный щит, 1947–1952 гг.. История Комиссии по атомной энергии США. Университетский парк: издательство Пенсильванского государственного университета. С. 380–385. ISBN  978-0-520-07187-2. OCLC  3717478.
42. Питер Галисон (1996). «5: Компьютерное моделирование и торговая зона». В Питере Галисоне, Дэвиде Дж. Стампе (ред.). Разобщенность науки: границы, контексты и сила. Stanford University Press. п. 135. ISBN  9780804725620.
43. Родос, Ричард (1995). Темное Солнце: Создание водородной бомбы. Нью-Йорк: Саймон и Шустер. стр.422 –424. ISBN  978-0-684-80400-2.
44. "Персональная биография Дж. Карсона Марка". Лос-Аламосская национальная лаборатория. Архивировано из оригинал 16 июля 2012 г.. Получено 22 октября 2011.
45. Teller, E .; С. Улам (9 марта 1951 г.). «Гетерокаталитические взрывы» (PDF). Отчет LANL LAMS-1225. Получено 2 ноября 2011.
46. Теллер, Э. (4 апреля 1951 г.), «Новое термоядерное устройство», Технический отчет LAMS-1230, Лос-Аламосская национальная лаборатория
47. Родос, Ричард (1995). Темное Солнце: Создание водородной бомбы. Нью-Йорк: Саймон и Шустер. стр.455 –464. ISBN  978-0-684-80400-2.
48. Хьюлетт, Ричард Дж .; Дункан, Фрэнсис (1969). Атомный щит, 1947–1952 гг.. История Комиссии по атомной энергии США. Университетский парк: издательство Пенсильванского государственного университета. С. 554–556. ISBN  978-0-520-07187-2. OCLC  3717478.
49. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.220–224. ISBN  9780684143910. OCLC  1528346.
50. Бете, Ханс А. (осень 1982 г.). «Перепечатка статьи 1954 года: комментарии к истории водородной бомбы» (PDF). Лос-Аламос Сайенс, № 6. Лос-Аламосская национальная лаборатория. Получено 3 ноября 2011.
51. Учии, Сошичи (22 июля 2003 г.). «Рецензия на мемуары Эдварда Теллера». Информационный бюллетень PHS. 52. Получено 13 августа 2012.
52. Швебер, С. С. (2000). В тени бомбы: Бете, Оппенгеймер и моральная ответственность ученого. Принстон: Издательство Принстонского университета. стр.166. ISBN  978-0-691-04989-2.
53. Паста, Джон; С. Улам (9 марта 1953 г.). «Эвристические исследования в задачах математической физики» (PDF). Отчет LANL LA-1557. Получено 21 ноября 2011.
54. Доксуа, Тьерри (2008). «Ферми, Паста, Улам и таинственная дама» (PDF). Физика сегодня. 6 (1): 55–57. arXiv:0801.1590. Bibcode:2008ФТ .... 61а..55Д. Дои:10.1063/1.2835154. S2CID  118607235. Получено 7 мая 2017.
55. Fermi, E .; J. Pasta; С. Улам (май 1955 г.). «Исследования нелинейных задач I» (PDF). Отчет LANL LA-1940. Получено 21 ноября 2011.
56. Портер, Мейсон А .; Забуски, Норман Дж .; Ху, Бэмби; Кэмпбелл, Дэвид К. (май – июнь 2009 г.). «Ферми, Паста, Улам и рождение экспериментальной математики» (PDF). Американский ученый. 97 (3): 214–221. Дои:10.1511/2009.78.214. Получено 20 ноября 2011.
57. Линдли, Дэвид (8 февраля 2013 г.). «В фокусе: ориентиры - компьютерное моделирование привело к открытию солитонов». Физика. 6 (15): 15. Bibcode:2013PhyOJ ... 6 ... 15л. Дои:10.1103 / Физика.6.15.
58. Longmier, C .; Ф. Рейнес; С. Улам (август 1955 г.). «Некоторые схемы ядерных двигателей» (PDF). Отчет LANL LAMS-2186. Получено 24 ноября 2011.
59. Улам, С. М. (1983). Приключения математика. Нью-Йорк: Сыновья Чарльза Скрибнера. стр.249–250. ISBN  9780684143910. OCLC  1528346.
60. Schreiber, R.E .; Улам, Станислав М .; Брэдбери, Норрис (1958). "Конгресс США, Объединенный комитет по атомной энергии: слушание 22 января 1958 г.". Движение в космическое пространство с помощью ядерной энергии. Типография правительства США. п. 47. Получено 25 ноября 2011.
61. Everett, C.J .; С. М. Улам (август 1955 г.). «О способе движения снарядов за счет внешних ядерных взрывов» (PDF). Отчет LANL LAMS-1955. Получено 24 ноября 2011.
62. «История проекта Орион». История Ориона. OrionDrive.com. 2008–2009. Получено 7 октября 2011.
63. Дайсон, Фримен (9 июля 1965 г.). «Смерть проекта». Наука. 149 (3680): 141–144. Bibcode:1965Научный ... 149..141D. Дои:10.1126 / science.149.3680.141. PMID  17734490.
64. Улам, С. М. (1961), "О некоторых статистических свойствах динамических систем", Труды 4-го симпозиума в Беркли по математической статистике и теории вероятностей, Berkeley CA, v 3, p 315: University of California Press
65. Авраам, Ральф (9 июля 2011 г.). «Энтропия изображения для дискретных динамических систем» (PDF). Калифорнийский университет в Санта-Крус. Получено 30 мая 2013.
66. Stein, P. R .; Станислав М. Улам (март 1959 г.). «Квадратичные преобразования. Часть I» (PDF). Отчет LANL LA-2305. Лос-Аламосская национальная лаборатория. Получено 26 ноября 2011.
67. "Станислав Улам". Американский институт физики. Архивировано из оригинал 2 июля 2015 г.. Получено 14 мая 2013.
68. Шрандт, Роберт Дж .; Станислав М. Улам (декабрь 1970 г.). «Некоторые элементарные попытки численного моделирования задач, касающихся скоростей эволюционных процессов» (PDF). Отчет LANL LA-4246. Лос-Аламосская национальная лаборатория. Получено 26 ноября 2011.
69. Бейер, Уильям А .; Темпл Ф. Смит; М. Л. Штейн; Станислав М. Улам (август 1972 г.). «Метрики в биологии, введение» (PDF). Отчет LANL LA-4973. Лос-Аламосская национальная лаборатория. Получено 26 ноября 2011.
70. "Документы Станислава М. Улама". Американское философское общество. Получено 14 мая 2013.
71. "Некролог Франсуазы Улам". Санта-Фе, Нью-Мексико. 30 апреля 2011 г.. Получено 12 декабря 2011.
72. «Станислав Улам» (PDF) (На французском). Получено 29 октября 2015.
73. Сборник научных трудов Пола А. Самуэльсона, т. III, стр. 683, MIT Press, 1966 г.
74. "Издания Станислава М. Улама" (PDF). Лос-Аламосская наука, № 15, 1987 г.. Лос-Аламосская национальная лаборатория. Получено 6 декабря 2011.
75. "Искать" Улам "на сайте AMS". Американское математическое общество. Получено 10 декабря 2011.
76. День после Троицы на IMDb
77. Экхардт, Роджер (1987). «Стэн Улам, Джон фон Нейман и метод Монте-Карло» (PDF). Лос-Аламос Сайенс. Лос-Аламосская национальная лаборатория. Получено 11 мар 2016.
78. Кейси, Томас М. (июнь 2011 г.). «Описание курса: Методы Монте-Карло для социологов». Межуниверситетский консорциум политических и социальных исследований. университет Мичигана. Получено 9 декабря 2011.
79. Поултер, Сьюзан Р. (зима 1998 г.). «Моделирование методом Монте-Карло в оценке экологических рисков» (PDF). Риск: здоровье, безопасность и окружающая среда. Университет Нью-Гэмпшира. Архивировано из оригинал (PDF) на 2016-03-06. Получено 13 сентября 2012.
80. Кляйн, Шелдон (23 мая 1966 г.). «Историческое изменение языка с использованием методов Монте-Карло» (PDF). Механический перевод и компьютерная лингвистика. 9 (3 и 4): 67–81. Получено 9 декабря 2011.
81. Earl, M. A .; Л. М. Ма (12 марта 2002 г.). «Повышение дозы электронного пучка под воздействием внешних магнитных полей: исследование Монте-Карло». Медицинская физика. 29 (4): 484–492. Bibcode:2002МедФ..29..484Э. Дои:10.1118/1.1461374. PMID  11991119. Получено 9 декабря 2011.
82. Людвиг, Джон (ноябрь 2011 г.). "Монте-Карло моделирование гонки Big10". ludwig.com. Получено 9 декабря 2011.
83. Кэмпбелл, Дональд Х. (17 марта 2010 г.). «Рождение нелинейной науки» (PDF). Американское физическое общество. Получено 8 декабря 2011.
84. "CNLS: признательность Мартина Крускала и Олвина Скотта". Лос-Аламосская национальная лаборатория. 2007 г.. Получено 8 декабря 2011.
85. «История Центра нелинейных исследований». Лос-Аламосская национальная лаборатория. Получено 8 декабря 2011.
86. "Ученые Улама в CNLS". Лос-Аламосская национальная лаборатория. Получено 8 декабря 2011.
87. "Фокус-проблема: проблема Ферми-Паста-Улам-Первые 50 лет". Хаос. 15 (1). Март 2005. Архивировано с оригинал на 2012-05-03. Получено 9 декабря 2011.
88. «50 лет проблемы Ферми-Паста-Улам: наследие, влияние и многое другое». 25-я Международная конференция CLNS. Лос-Аламосская национальная лаборатория. 16–20 мая 2005 г.. Получено 9 декабря 2011.
89. "Домашняя страница ежеквартального журнала" Улам ". Университет Флориды. Получено 24 декабря 2011.
90. Дикс, Хулио Г. (25–27 июня 2004 г.), «Некоторые аспекты ведения бесплатного электронного журнала» (PDF), в Becker, Hans (ed.), Новые разработки в электронной публикации, Стокгольм: Европейский конгресс математиков; ECM4 Satellite Conference, стр. 41–43, ISBN  978-3-88127-107-3, получено 5 января 2013
91. "Список спикеров коллоквиума улам". Университет Флориды, факультет математики. Получено 24 декабря 2011.
92. "Конференция столетия Улама". Университет Флориды. 10–11 марта 2009 г. Архивировано с оригинал 24 апреля 2012 г.. Получено 24 декабря 2011.
93. Гоуд, Уолтер Б. (1987). «Анализ последовательности: вклад Улама в молекулярную генетику» (PDF). Лос-Аламос Сайенс. Лос-Аламосская национальная лаборатория. Получено 28 декабря 2011.
94. Новый вид науки [1]
95. Новый вид науки [2]
96. Санкофф, Дэвид (2000). «Раннее введение динамического программирования в вычислительную биологию». Биоинформатика. 16 (1): 41–47. Дои:10.1093 / биоинформатика / 16.1.41. PMID  10812476.
97. Бейер, Уильям А .; Питер Х. Селлерс; Майкл С. Уотерман (1985). "Вклад Станислава М. Улама в теоретическую биологию" (PDF). Письма по математической физике. 10 (2–3): 231–242. Bibcode:1985ЛМАФ..10..231Б. CiteSeerX  10.1.1.78.4790. Дои:10.1007 / bf00398163. S2CID  2791811. Архивировано из оригинал (PDF) 27 сентября 2011 г.. Получено 5 декабря 2011.
98. Купер, Несия Грант. "Станислав Улам 1909–1984". Лос-Аламосская наука, № 15, 1987 г.. Лос-Аламосская национальная лаборатория. Получено 6 декабря 2011.
99. Улам, С. М. (1990). А. Р. Беднарек; Франсуаза Улам (ред.). Аналогии между аналогиями. Беркли: Калифорнийский университет Press. ISBN  978-0-520-05290-1. Получено 24 декабря 2011.
100. Эпштейн, Соня (29 июня 2017 г.). «Приключения математика». Sloan Science & Film.

внешние ссылки

• Аудиоинтервью 1979 года со Станиславом Уламом Мартина Шервина Голоса Манхэттенского проекта
• Аудио-интервью 1965 года со Станиславом Уламом Ричарда Родса Голоса Манхэттенского проекта
• "Издания Станислава М. Улама" (PDF). Лос-Аламос Сайенс (Специальный выпуск): 313. 1987. ISSN  0273-7116.