Модель Кокса – Ингерсолла – Росса - Cox–Ingersoll–Ross model

Три траектории процессов CIR

В математические финансы, то Модель Кокса – Ингерсолла – Росса (CIR) описывает эволюцию процентные ставки. Это разновидность «однофакторной модели» (модель краткосрочной ставки ), поскольку он описывает движение процентных ставок как обусловленное только одним источником рыночный риск. Модель может быть использована при оценке производные по процентной ставке. Он был представлен в 1985 году Джон К. Кокс, Джонатан Э. Ингерсолл и Стивен А. Росс как продолжение Модель Васичека.

Модель

Процесс CIR

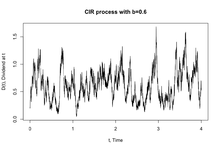
Модель CIR определяет, что мгновенная процентная ставка ${displaystyle r_{t}}$ следует за стохастическое дифференциальное уравнение, также называемый процессом CIR:

${displaystyle dr_{t}=a(b-r_{t}),dt+sigma {sqrt {r_{t}}},dW_{t}}$

где ${displaystyle W_{t}}$ это Винеровский процесс (моделирование случайного фактора рыночного риска) и ${displaystyle a}$, ${displaystyle b}$, и ${displaystyle sigma ,}$ являются параметры. Параметр ${displaystyle a}$ соответствует скорости приспособления к среднему ${displaystyle b}$, и ${displaystyle sigma ,}$ к волатильности. Коэффициент дрейфа, ${displaystyle a(b-r_{t})}$, точно такая же, как в модели Васичека. Это обеспечивает значит возвращение процентной ставки к долгосрочной стоимости ${displaystyle b}$, со скоростью настройки, регулируемой строго положительным параметром ${displaystyle a}$.

В среднеквадратичное отклонение фактор ${displaystyle sigma {sqrt {r_{t}}}}$, избегает возможности отрицательных процентных ставок для всех положительных значений ${displaystyle a}$ и ${displaystyle b}$. Нулевая процентная ставка также не допускается, если условие

${displaystyle 2abgeq sigma ^{2},}$

встречается. В более общем плане, когда ставка (${displaystyle r_{t}}$) близко к нулю, стандартное отклонение (${displaystyle sigma {sqrt {r_{t}}}}$) также становится очень малым, что ослабляет влияние случайного скачка на скорость. Следовательно, когда скорость приближается к нулю, в ее эволюции доминирует фактор дрейфа, который толкает скорость вверх (в сторону равновесие ).

Этот процесс можно определить как сумму квадратов Процесс Орнштейна – Уленбека. CIR - это эргодический процесс и обладает стационарным распределением. Тот же процесс используется в Модель Хестона для моделирования стохастической волатильности.

Распределение

• Будущее распространение

Распределение будущих значений процесса CIR можно вычислить в закрытой форме:

${displaystyle r_{t+T}={frac {Y}{2c}},}$

где ${displaystyle c={frac {2a}{(1-e^{-aT})sigma ^{2}}}}$, и Y это нецентральное распределение хи-квадрат с ${displaystyle {frac {4ab}{sigma ^{2}}}}$ степень свободы и параметр нецентральности ${displaystyle 2cr_{t}e^{-aT}}$. Формально функция плотности вероятности:

${displaystyle f(r_{t+T};r_{t},a,b,sigma )=c,e^{-u-v}left({frac {v}{u}}ight)^{q/2}I_{q}(2{sqrt {uv}}),}$

где ${displaystyle q={frac {2ab}{sigma ^{2}}}-1}$, ${displaystyle u=cr_{t}e^{-aT}}$, ${displaystyle v=cr_{t+T}}$, и ${displaystyle I_{q}(2{sqrt {uv}})}$ - модифицированная функция Бесселя первого вида порядка ${displaystyle q}$.

• Асимптотическое распределение

Из-за обращения к среднему, когда время становится большим, распределение ${displaystyle r_{infty }}$ приблизится к гамма-распределение с плотностью вероятности:

${displaystyle f(r_{infty };a,b,sigma )={frac {eta ^{alpha }}{Gamma (alpha )}}r_{infty }^{alpha -1}e^{-eta r_{infty }},}$

где ${displaystyle eta =2a/sigma ^{2}}$ и ${displaystyle alpha =2ab/sigma ^{2}}$.

Вывод асимптотического распределения.

Чтобы получить асимптотическое распределение ${displaystyle p_{infty }}$ для модели CIR мы должны использовать Уравнение Фоккера-Планка: ${displaystyle {partial p over {partial t}}+{partial over {partial r}}[a(b-r)p]={1 over {2}}sigma ^{2}{partial ^{2} over {partial r^{2}}}(rp)}$ Наш интерес представляет частный случай, когда ${displaystyle partial _{t}pightarrow 0}$, что приводит к упрощенному уравнению: ${displaystyle a(b-r)p_{infty }={1 over {2}}sigma ^{2}left(p_{infty }+r{dp_{infty } over {dr}}ight)}$ Определение ${displaystyle alpha =2ab/sigma ^{2}}$ и ${displaystyle eta =2a/sigma ^{2}}$ а перестановка членов приводит к уравнению: ${displaystyle {alpha -1 over {r}}-eta ={d over {dr}}log p_{infty }}$ Интеграция показывает нам, что: ${displaystyle p_{infty }propto r^{alpha -1}e^{-eta r}}$ За пределами диапазона ${displaystyle p_{infty }in (0,infty ]}$, эта плотность описывает гамма-распределение. Следовательно, асимпотическое распределение модели CIR - это гамма-распределение.

Характеристики

• Значит возвращение,
• Зависящая от уровня волатильность (${displaystyle sigma {sqrt {r_{t}}}}$),
• Для данного положительного ${displaystyle r_{0}}$ процесс никогда не коснется нуля, если ${displaystyle 2abgeq sigma ^{2}}$; в противном случае он может случайно коснуться нулевой точки,
• ${displaystyle operatorname {E} [r_{t}mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})}$, поэтому долгосрочное среднее значение ${displaystyle b}$,
• ${displaystyle operatorname {Var} [r_{t}mid r_{0}]=r_{0}{frac {sigma ^{2}}{a}}(e^{-at}-e^{-2at})+{frac {bsigma ^{2}}{2a}}(1-e^{-at})^{2}.}$

Калибровка

• Обычный метод наименьших квадратов

Непрерывный SDE можно дискретизировать следующим образом

${displaystyle r_{t+Delta t}-r_{t}=a(b-r_{t}),Delta t+sigma ,{sqrt {r_{t}Delta t}}varepsilon _{t},}$

что эквивалентно

${displaystyle {frac {r_{t+Delta t}-r_{t}}{{sqrt {r}}_{t}}}={frac {abDelta t}{{sqrt {r}}_{t}}}-a{sqrt {r}}_{t}Delta t+sigma ,{sqrt {Delta t}}varepsilon _{t},}$

предоставлена ${displaystyle varepsilon _{t}}$ это n.i.i.d. (0,1). Это уравнение можно использовать для линейной регрессии.

• Оценка Мартингейла
• Максимальная вероятность

Моделирование

Стохастическое моделирование процесса CIR можно достичь двумя вариантами:

• Дискретность
• Точный

Цены на облигации

При условии отсутствия арбитража цена облигации может оцениваться с использованием этого процесса процентной ставки. Цена облигации экспоненциально связана с процентной ставкой:

${displaystyle P(t,T)=A(t,T)exp(-B(t,T)r_{t})!}$

где

${displaystyle A(t,T)=left({frac {2hexp((a+h)(T-t)/2)}{2h+(a+h)(exp((T-t)h)-1)}}ight)^{2ab/sigma ^{2}}}$

${displaystyle B(t,T)={frac {2(exp((T-t)h)-1)}{2h+(a+h)(exp((T-t)h)-1)}}}$

${displaystyle h={sqrt {a^{2}+2sigma ^{2}}}}$

Расширения

Процесс CIR - это частный случай диффузия базового аффинного скачка, что по-прежнему позволяет выражение в закрытой форме по ценам облигаций. В модель можно ввести изменяющиеся во времени функции, заменяющие коэффициенты, чтобы привести ее в соответствие с заранее заданной временной структурой процентных ставок и, возможно, волатильности. Самый общий подход описан в Maghsoodi (1996). Более гибкий подход представлен в работе Бриго и Меркурио (2001b), где к модели добавляется внешний временной сдвиг для согласованности с входной временной структурой ставок. Существенное расширение модели CIR на случай стохастического среднего и стохастической волатильности дается выражением Лин Чен (1996) и известен как Чен модель. Более недавнее расширение - это так называемый CIR # Орландо, Мининни и Буфало (2018,^[1] 2019 ^[2], ^[3]).

Смотрите также

• Модель Халла – Уайта
• Модель Васичека
• Чен модель

Рекомендации

1. Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (2018). «Новый подход к моделированию краткосрочных ставок CIR». Новые методы моделирования с фиксированным доходом. Вклад в науку управления. Издательство Springer International: 35–43. Дои:10.1007/978-3-319-95285-7_2. ISBN  978-3-319-95284-0.
2. Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (1 января 2019 г.). «Новый подход к прогнозированию рыночных процентных ставок с помощью модели CIR». Исследования в области экономики и финансов. перед печатью (перед печатью). Дои:10.1108 / SEF-03-2019-0116. ISSN  1086-7376.
3. Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (19 августа 2019 г.). «Калибровка процентных ставок с помощью модели CIR». Журнал риск-финансирования. 20 (4): 370–387. Дои:10.1108 / JRF-05-2019-0080. ISSN  1526-5943.

Дальнейшие ссылки

• Халл, Джон С. (2003). Опционы, фьючерсы и другие производные инструменты. Река Верхний Сэдл, Нью-Джерси: Prentice Hall. ISBN  0-13-009056-5.
• Кокс, Дж. К., Дж. Ингерсолл и С.А. Росс (1985). «Теория временной структуры процентных ставок». Econometrica. 53 (2): 385–407. Дои:10.2307/1911242. JSTOR  1911242.
• Магсуди, Ю. (1996). «Решение расширенной срочной структуры CIR и оценки опционов на облигации». Математические финансы. 6 (6): 89–109. Дои:10.1111 / j.1467-9965.1996.tb00113.x.
• Дамиано Бриго; Фабио Меркурио (2001). Модели процентных ставок - теория и практика с улыбкой, инфляция и кредит (2-е изд., 2006 г.). Springer Verlag. ISBN  978-3-540-22149-4.
• Бриго, Дамиано; Фабио Меркурио (2001b). «Расширение детерминированных сдвигов аналитически податливых и однородных по времени моделей коротких ставок». Финансы и стохастика. 5 (3): 369–388. Дои:10.1007 / PL00013541. S2CID  35316609.
• Библиотека с открытым исходным кодом, реализующая процесс CIR на Python
• Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (2020). «Прогнозирование процентных ставок с помощью моделей Vasicek и CIR: метод разделения». Журнал прогнозирования. 39 (4): 569–579. arXiv:1901.02246. Дои:10.1002 / за 2642. ISSN  1099–131X. S2CID  126507446.