Тип распределения вероятностей
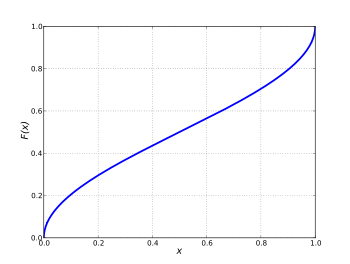
В теория вероятности, то распределение арксинусов это распределение вероятностей чей кумулятивная функция распределения является

для 0 ≤Икс ≤ 1, и чья функция плотности вероятности является

на (0, 1). Стандартное распределение арксинусов является частным случаем бета-распространение с α = β = 1/2. То есть, если  стандартное распределение арксинусов, то
стандартное распределение арксинусов, то  . В более широком смысле, распределение арксинусов является частным случаем Распределение Пирсона типа I.
. В более широком смысле, распределение арксинусов является частным случаем Распределение Пирсона типа I.
Появляется распределение арксинуса
Обобщение
Арксинус - ограниченная поддержка| Параметры |  |
|---|
| Поддерживать | ![х в [а, б]](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) |
|---|
| PDF |  |
|---|
| CDF |  |
|---|
| Иметь в виду |  |
|---|
| Медиана |  |
|---|
| Режим |  |
|---|
| Дисперсия |  |
|---|
| Асимметрия |  |
|---|
| Бывший. эксцесс |  |
|---|
Произвольная ограниченная поддержка
Распространение может быть расширено за счет любой ограниченной поддержки от а ≤ Икс ≤ б простым преобразованием

за а ≤ Икс ≤ б, и чья функция плотности вероятности является

на (а, б).
Фактор формы
Обобщенное стандартное распределение арксинуса на отрезке (0,1) с функцией плотности вероятности

также частный случай бета-распространение с параметрами  .
.
Обратите внимание, что когда  общее распределение арксинусов сводится к стандартному распределению, указанному выше.
общее распределение арксинусов сводится к стандартному распределению, указанному выше.
Характеристики
- Распределение арксинуса замкнуто при трансляции и масштабировании положительным фактором
- Если

- Квадрат арксинусного распределения по (-1, 1) имеет арксинусное распределение по (0, 1)
- Если

Характеристическая функция
Характеристическая функция распределения арксинуса есть конфлюэнтная гипергеометрическая функция и дан как  .
.
Связанные дистрибутивы
- Если U и V равны i.i.d униформа (−π, π) случайных величин, то
 ,
,  ,
,  ,
,  и
и  у всех есть
у всех есть  распределение.
распределение. - Если
 - обобщенное распределение арксинуса с параметром формы
- обобщенное распределение арксинуса с параметром формы  на конечном интервале [a, b], то
на конечном интервале [a, b], то 
Смотрите также
Рекомендации
|
|---|
Дискретный одномерный
с конечной опорой | |
|---|
Дискретный одномерный
с бесконечной поддержкой | |
|---|
Непрерывный одномерный
поддерживается на ограниченном интервале | |
|---|
Непрерывный одномерный
поддерживается на полубесконечном интервале | |
|---|
Непрерывный одномерный
поддерживается на всей реальной линии | |
|---|
Непрерывный одномерный
с поддержкой, тип которой варьируется | |
|---|
| Смешанная непрерывно-дискретная одномерная | |
|---|
| Многовариантный (совместный) | |
|---|
| Направленный | |
|---|
| Вырожденный и единственное число | |
|---|
| Семьи | |
|---|


![х дюйм [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)














![х в [а, б]](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

















