Треугольное распределение - Triangular distribution

Треугольная

Функция плотности вероятности
Кумулятивная функция распределения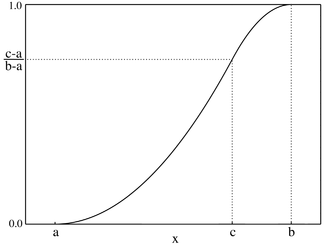
Параметры	${\displaystyle a:~a\in (-\infty ,\infty )}$ ${\displaystyle b:~a<b\,}$ ${\displaystyle c:~a\leq c\leq b\,}$
Поддержка	${\displaystyle a\leq x\leq b\!}$
PDF	${\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{for }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}}}$
CDF	${\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}}$
Значить	${\displaystyle {\frac {a+b+c}{3}}}$
Медиана	${\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}$
Режим	${\displaystyle c\,}$
Дисперсия	${\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}$
Асимметрия	${\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}$
Ex. эксцесс	${\displaystyle -{\frac {3}{5}}}$
Энтропия	${\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}$
MGF	${\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}$
CF	${\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}$

В теория вероятности и статистика, то треугольное распределение является непрерывным распределение вероятностей с нижним пределом а, верхний предел б и режим c, где а < б и а ≤ c ≤ б.

Особые случаи

Режим на грани

Распределение упрощается, когда c = а или c = б. Например, если а = 0, б = 1 и c = 1, то PDF и CDF становиться:

${\displaystyle \left.{\begin{array}{rl}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{array}}\right\}{\text{ for }}0\leq x\leq 1}$

${\displaystyle {\begin{aligned}\operatorname {E} (X)&={\frac {2}{3}}\\[8pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}$

Распределение абсолютной разности двух стандартных равномерных переменных

Это раздача для а = 0, б = 1 и c = 0 - распределение Икс = |Икс₁ − Икс₂|, где Икс₁, Икс₂ две независимые случайные величины со стандартными равномерное распределение.

${\displaystyle {\begin{aligned}f(x)&=2-2x{\text{ for }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ for }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}$

Симметричное треугольное распределение

Симметричный случай возникает, когда c = (а + б) / 2. В этом случае альтернативный вид функции распределения:

${\displaystyle {\begin{aligned}f(x)&={\frac {(b-c)-|c-x|}{(b-c)^{2}}}\\[6pt]\end{aligned}}}$

Распределение среднего двух стандартных однородных переменных

Это раздача для а = 0, б = 1 и c = 0,5 - мода (т.е. пик) находится точно в середине интервала - соответствует распределению среднего двух стандартных однородных переменных, т. Е. Распределению Икс = (Икс₁ + Икс₂) / 2, где Икс₁, Икс₂ две независимые случайные величины со стандартными равномерное распределение в [0, 1].^[1]

${\displaystyle f(x)={\begin{cases}4x&{\text{for }}0\leq x<{\frac {1}{2}}\\4(1-x)&{\text{for }}{\frac {1}{2}}\leq x\leq 1\end{cases}}}$

${\displaystyle F(x)={\begin{cases}2x^{2}&{\text{for }}0\leq x<{\frac {1}{2}}\\2x^{2}-(2x-1)^{2}&{\text{for }}{\frac {1}{2}}\leq x\leq 1\end{cases}}}$

${\displaystyle {\begin{aligned}E(X)&={\frac {1}{2}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{24}}\end{aligned}}}$

Генерация случайных величин с треугольным распределением

Учитывая случайную вариацию U взяты из равномерное распределение в интервале (0, 1), то вариация

${\displaystyle X={\begin{cases}a+{\sqrt {U(b-a)(c-a)}}&{\text{ for }}0<U<F(c)\\&\\b-{\sqrt {(1-U)(b-a)(b-c)}}&{\text{ for }}F(c)\leq U<1\end{cases}}}$^[2]

где ${\displaystyle F(c)=(c-a)/(b-a)}$, имеет треугольное распределение с параметрами ${\displaystyle a,b}$ и ${\displaystyle c}$. Это можно получить из кумулятивной функции распределения.

Использование раздачи

Смотрите также: Трехбалльная оценка

Треугольное распределение обычно используется как субъективное описание совокупности, для которой имеется лишь ограниченный набор данных, особенно в случаях, когда взаимосвязь между переменными известна, но данных мало (возможно, из-за высокой стоимости сбора). основанный на знании минимума и максимума и «вдохновенном предположении»^[3] что касается модального значения. По этим причинам треугольное распределение было названо распределением "недостатка знаний".

Бизнес-симуляции

Поэтому треугольное распределение часто используется в принятие бизнес-решений, особенно в симуляции. Как правило, когда о распространение результата (скажем, только его наименьшее и наибольшее значения), можно использовать равномерное распределение. Но если известен также наиболее вероятный исход, то его можно смоделировать с помощью треугольного распределения. См., Например, под корпоративные финансы.

Управление проектом

Треугольное распределение вместе с Распределение PERT, также широко используется в управление проектом (как вход в ПЕРТ и, следовательно метод критического пути (CPM)) для моделирования событий, которые происходят в интервале, определяемом минимальным и максимальным значением.

Аудио дизеринг

Симметричное треугольное распределение обычно используется в дизеринг звука, где она называется TPDF (треугольная функция плотности вероятности).

Смотрите также

• Трапециевидное распределение
• Томас Симпсон
• Трехбалльная оценка
• Пятизначное резюме
• Семизначное резюме
• Треугольная функция
• Центральная предельная теорема - Треугольное распределение часто возникает в результате сложения двух однородных случайных величин. Другими словами, треугольное распределение часто (не всегда) является результатом первой итерации процесса суммирования центральной предельной теоремы (т.е. ${\textstyle n=2}$). В этом смысле треугольное распределение может иногда возникать естественным образом. Если этот процесс суммирования большего количества случайных величин продолжается (т.е. ${\textstyle n\geq 3}$), то распределение станет все более колоколообразным.
• Распределение Ирвина – Холла - Использование распределения Ирвина – Холла - простой способ сгенерировать треугольное распределение.
• Распределение Бейтса - Подобно распределению Ирвина – Холла, но с масштабированием значений обратно в диапазон от 0 до 1. Полезно для вычисления треугольного распределения, которое впоследствии можно масштабировать и сдвигать для создания других треугольных распределений за пределами диапазона от 0 до 1.

использованная литература

1. Помимо бета-версии: другие непрерывные семейства дистрибутивов с ограниченной поддержкой и приложениями. Самуэль Коц и Йохан Рене ван Дорп. https://books.google.de/books?id=JO7ICgAAQBAJ&lpg=PA1&dq=chapter%201%20dig%20out%20suitable%20substitutes%20of%20the%20beta%20distribution%20one%20of%20our%20goals&pg=PA3#v= одна страница & q & f = false
2. https://web.archive.org/web/20140407075018/http://www.asianscientist.com/books/wp-content/uploads/2013/06/5720_chap1.pdf
3. «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2006-09-23. Получено 2006-09-23.

внешние ссылки

• Вайсштейн, Эрик В. «Треугольное распределение». MathWorld.
• Распределение треугольников, solutionsciences.org
• Треугольное распределение, brighton-webs.co.uk