Канторовское распределение - Cantor distribution - Wikipedia

Кантор

Кумулятивная функция распределения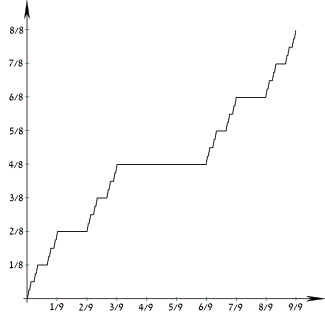
Параметры	никто
Поддерживать	Кантор набор
PMF	никто
CDF	Функция Кантора
Иметь в виду	1/2
Медиана	где угодно в [1/3, 2/3]
Режим	н / д
Дисперсия	1/8
Асимметрия	0
Бывший. эксцесс	−8/5
MGF	${\displaystyle e^{t/2}\prod _{k=1}^{\infty }\cosh \left({\frac {t}{3^{k}}}\right)}$
CF	${\displaystyle e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\right)}$

В Канторовское распределение это распределение вероятностей чей кумулятивная функция распределения это Функция Кантора.

Этот дистрибутив не имеет функция плотности вероятности ни функция массы вероятности, поскольку, хотя его кумулятивная функция распределения является непрерывная функция, распределение не абсолютно непрерывный относительно Мера Лебега, и не имеет точечных масс. Таким образом, это ни дискретное, ни абсолютно непрерывное распределение вероятностей, ни их смесь. Скорее это пример сингулярное распределение.

Его кумулятивная функция распределения непрерывна везде, но почти везде горизонтальна, поэтому иногда ее называют Дьявольская лестница, хотя этот термин имеет более общее значение.

Характеристика

В поддерживать распределения Кантора является Кантор набор, само пересечение множеств (счетно бесконечно много):

${\displaystyle {\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1]\\[8pt]C_{5}={}&\cdots \end{aligned}}}$

Распределение Кантора - это уникальное распределение вероятностей, для которого для любого C_т (т ∈ {0, 1, 2, 3, ...}) вероятность определенного интервала в C_т со случайной величиной, распределенной по Кантору, тождественно 2^−т на каждом из 2^т интервалы.

Моменты

Из симметрии легко увидеть, что для случайная переменная Икс имея это распределение, его ожидаемое значение E (Икс) = 1/2, и что все нечетные центральные моменты Икс равны 0.

В закон полной дисперсии можно использовать для поиска отклонение var (Икс), следующее. Для указанного выше набора C₁, позволять Y = 0, если Икс ∈ [0,1 / 3], и 1, если Икс ∈ [2 / 3,1]. Потом:

${\displaystyle {\begin{aligned}\operatorname {var} (X)&=\operatorname {E} (\operatorname {var} (X\mid Y))+\operatorname {var} (\operatorname {E} (X\mid Y))\\&={\frac {1}{9}}\operatorname {var} (X)+\operatorname {var} \left\{{\begin{matrix}1/6&{\mbox{with probability}}\ 1/2\\5/6&{\mbox{with probability}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var} (X)+{\frac {1}{9}}\end{aligned}}}$

Отсюда получаем:

${\displaystyle \operatorname {var} (X)={\frac {1}{8}}.}$

Выражение в закрытой форме для любого четного центральный момент можно найти, предварительно получив четное кумулянты^[1]

${\displaystyle \kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!}$

куда B_2п это 2пth Число Бернулли, а потом выражая моменты как функции кумулянтов.

Рекомендации

1. Моррисон, Кент (23 июля 1998 г.). «Случайные блуждания с убывающими шагами» (PDF). Департамент математики Калифорнийского политехнического государственного университета. Получено 2007-02-16.

дальнейшее чтение

• Hewitt, E .; Стромберг, К. (1965). Реальный и абстрактный анализ. Берлин-Гейдельберг-Нью-Йорк: Springer-Verlag. В нем, как и в других стандартных текстах, есть функция Кантора и ее односторонние производные.
• Ху, Тянь-Ю; Лау, Ка Синг (2002). «Фурье-асимптотика мер канторовского типа на бесконечности». Proc. A.M.S. 130 (9). С. 2711–2717. Это более современный текст, чем другие тексты в этом списке литературы.
• Книл, О. (2006). Теория вероятностей и случайные процессы. Индия: зарубежная пресса.
• Маттилла, П. (1995). Геометрия множеств в евклидовых пространствах. Сан-Франциско: Издательство Кембриджского университета. Здесь есть более продвинутый материал по фракталам.