Отрицательное гипергеометрическое распределение - Negative hypergeometric distribution - Wikipedia

Отрицательный гипергеометрический

Вероятностная функция масс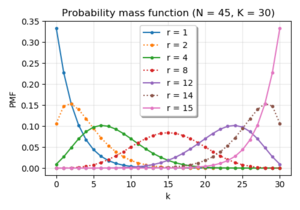
Кумулятивная функция распределения
Параметры	${\displaystyle N\in \left\{0,1,2,\dots \right\}}$ - общее количество элементов ${\displaystyle K\in \left\{0,1,2,\dots ,N\right\}}$ - общее количество элементов успеха ${\displaystyle r\in \left\{0,1,2,\dots ,N-K\right\}}$ - количество сбоев при остановке эксперимента
Поддерживать	${\displaystyle k\in \left\{0,\,\dots ,\,K\right\}}$ - количество успехов при остановке эксперимента.
PMF	${\displaystyle {\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}}$
Иметь в виду	${\displaystyle r{\frac {K}{N-K+1}}}$
Дисперсия	${\displaystyle r{\frac {(N+1)K}{(N-K+1)(N-K+2)}}[1-{\frac {r}{N-K+1}}]}$

В теория вероятности и статистика, то отрицательное гипергеометрическое распределение описывает вероятности при выборке из конечной совокупности без замены, в которой каждая выборка может быть разделена на две взаимоисключающие категории, такие как годен / не прошел, мужской / женский или занятый / безработный. Поскольку случайный выбор производится из совокупности, каждый последующий розыгрыш уменьшает популяцию, что приводит к изменению вероятности успеха с каждым розыгрышем. В отличие от стандартного гипергеометрическое распределение, который описывает количество успехов в фиксированном размере выборки, в отрицательном гипергеометрическом распределении выборки отбираются до ${\displaystyle r}$ отказов обнаружены, а распределение описывает вероятность нахождения ${\displaystyle k}$ успехов в таком образце. Другими словами, отрицательное гипергеометрическое распределение описывает вероятность ${\displaystyle k}$ успехов в выборке с точно ${\displaystyle r}$ неудачи.

Определение

Есть ${\displaystyle N}$ элементы, из которых ${\displaystyle K}$ определяются как «успехи», а остальные как «неудачи».

Элементы рисуются один за другим, без замены, пока ${\displaystyle r}$ встречаются сбои. Затем розыгрыш останавливается, и число ${\displaystyle k}$ успехов засчитывается. Отрицательное гипергеометрическое распределение, ${\displaystyle NHG_{N,K,r}(k)}$ это дискретное распределение этого ${\displaystyle k}$.

^[1]

Результат требует, чтобы мы наблюдали ${\displaystyle k}$ успехи в ${\displaystyle (k+r-1)}$ привлекает и ${\displaystyle (k+r){\text{-th}}}$ бит должен быть неудачным. Вероятность первого может быть найдена прямым применением гипергеометрическое распределение ${\displaystyle (HG_{N,K,k+r-1}(k))}$ а вероятность последнего - это просто количество оставшихся отказов. ${\displaystyle (=N-K-(r-1))}$ делится на размер оставшейся части населения ${\displaystyle (=N-(k+r-1)}$. Вероятность иметь ровно ${\displaystyle k}$ успехов до ${\displaystyle r{\text{-th}}}$ сбой (т. е. рисование останавливается, как только образец включает заранее определенное количество ${\displaystyle r}$ отказов) тогда является произведением этих двух вероятностей:

${\displaystyle {\frac {{\binom {K}{k}}{\binom {N-K}{k+r-1-k}}}{\binom {N}{k+r-1}}}\cdot {\frac {N-K-(r-1)}{N-(k+r-1)}}={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}.}$

Следовательно, случайная переменная следует отрицательному гипергеометрическому распределению, если его функция массы вероятности (pmf) определяется как

${\displaystyle f(k;N,K,r)\equiv \Pr(X=k)={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}\quad {\text{for }}k=0,1,2,\dotsc ,K}$

куда

• ${\displaystyle N}$ это численность населения,
• ${\displaystyle K}$ количество успешных состояний в популяции,
• ${\displaystyle r}$ количество отказов,
• ${\displaystyle k}$ количество наблюдаемых успехов,
• ${\displaystyle a \choose b}$ это биномиальный коэффициент

По замыслу вероятности в сумме равны 1. Однако, если мы хотим показать это явно, мы имеем:

${\displaystyle \sum _{k=0}^{K}\Pr(X=k)=\sum _{k=0}^{K}{\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}={\frac {1}{N \choose K}}\sum _{k=0}^{K}{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}={\frac {1}{N \choose K}}{N \choose K}=1,}$

где мы это использовали,

${\displaystyle {\begin{aligned}\sum _{j=0}^{k}{\binom {j+m}{j}}{\binom {n-m-j}{k-j}}&=\sum _{j=0}^{k}(-1)^{j}{\binom {-m}{j}}(-1)^{k-j}{\binom {k-n-(-m)}{k-j}}\\&=(-1)^{k}{\binom {k-n}{k}}=(-1)^{k}{\binom {k-(n+1)-1}{k}}={\binom {n+1}{k}},\end{aligned}}}$

который может быть получен с помощью биномиальная идентичность, ${\displaystyle {{n \choose k}=(-1)^{k}{k-n-1 \choose k}}}$, а Тождество Чу – Вандермонда, ${\displaystyle \sum _{j=0}^{k}{\binom {m}{j}}{\binom {n-m}{k-j}}={\binom {n}{k}}}$, что справедливо для любых комплексных значений ${\displaystyle m}$ и ${\displaystyle n}$ и любое неотрицательное целое число ${\displaystyle k}$.

Отношения ${\displaystyle \sum _{j=0}^{k}{\binom {j+m}{j}}{\binom {n-m-j}{k-j}}={\binom {n+1}{k}}}$ также можно найти, изучив коэффициент ${\displaystyle x^{k}}$ в расширении ${\displaystyle {\frac {1}{(1-x)^{m+1}}}{\frac {1}{(1-x)^{n-m-k+1}}}={\frac {1}{(1-x)^{n-k+2}}}}$, с помощью Биномиальный ряд Ньютона.

Ожидание

При подсчете числа ${\displaystyle k}$ успехов до ${\displaystyle r}$ неудач, ожидаемое количество успехов ${\displaystyle {\frac {rK}{N-K+1}}}$ и может быть получен следующим образом.

${\displaystyle {\begin{aligned}E[X]&=\sum _{k=0}^{K}k\Pr(X=k)=\sum _{k=0}^{K}k{\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{\frac {(k+r)}{r}}{{k+r-1} \choose {r-1}}{{N-r-k} \choose {K-k}}\right]-r\\&={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r} \choose {r}}{{N-r-k} \choose {K-k}}\right]-r={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r} \choose {k}}{{N-r-k} \choose {K-k}}\right]-r\\&={\frac {r}{N \choose K}}\left[{{N+1} \choose K}\right]-r={\frac {rK}{N-K+1}},\end{aligned}}}$

где мы использовали отношения ${\displaystyle \sum _{j=0}^{k}{\binom {j+m}{j}}{\binom {n-m-j}{k-j}}={\binom {n+1}{k}}}$, который мы вывели выше, чтобы показать, что отрицательное гипергеометрическое распределение было правильно нормализовано.

Дисперсия

Дисперсию можно получить с помощью следующего расчета.

${\displaystyle {\begin{aligned}E[X^{2}]&=\sum _{k=0}^{K}k^{2}\Pr(X=k)=\left[\sum _{k=0}^{K}(k+r)(k+r+1)\Pr(X=k)\right]-(2r+1)E[X]-r^{2}-r\\&={\frac {r(r+1)}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r+1} \choose {k+1}}{{N+1-(r+1)-k} \choose {K-k}}\right]-(2r+1)E[X]-r^{2}-r\\&={\frac {r(r+1)}{N \choose K}}\left[{{N+2} \choose K}\right]-(2r+1)E[X]-r^{2}-r={\frac {rK(N-r+Kr+1)}{(N-K+1)(N-K+2)}}\end{aligned}}}$

Тогда дисперсия равна ${\displaystyle {\textrm {Var}}[X]=E[X^{2}]-\left(E[X]\right)^{2}={\frac {rK(N+1)(N-K-r+1)}{(N-K+1)^{2}(N-K+2)}}}$

Связанные дистрибутивы

Если рисунок останавливается после постоянного числа ${\displaystyle n}$ ничьих (независимо от количества неудач), то количество успехов имеет гипергеометрическое распределение, ${\displaystyle HG_{N,K,n}(k)}$. Эти две функции связаны следующим образом:^[1]

${\displaystyle NHG_{N,K,r}(k)=1-HG_{N,N-K,k+r}(r-1)}$

Отрицательно-гипергеометрическое распределение (например, гипергеометрическое распределение) имеет дело с розыгрышами без замены, так что вероятность успеха в каждом розыгрыше разная. Напротив, отрицательно-биномиальное распределение (например, биномиальное распределение) имеет дело с ничьей. с заменой, так что вероятность успеха одинакова, а испытания независимы. В следующей таблице приведены четыре распределения, связанных с элементами чертежа:

	С заменами	Никаких замен
Количество успехов при постоянном количестве розыгрышей	биномиальное распределение	гипергеометрическое распределение
Количество успехов при постоянном количестве неудач	отрицательное биномиальное распределение	отрицательное гипергеометрическое распределение

Рекомендации

1. Отрицательное гипергеометрическое распределение в энциклопедии математики.