Гильбертово пространство - Hilbert space

В математический концепция Гильбертово пространство, названный в честь Дэвид Гильберт, обобщает понятие Евклидово пространство. Он расширяет методы векторная алгебра и исчисление из двумерного Евклидова плоскость и трехмерное пространство в пространства с любым конечным или бесконечным числом размеры. Гильбертово пространство - это абстрактное векторное пространство обладающий структура из внутренний продукт что позволяет измерять длину и угол. Кроме того, гильбертовы пространства полный: достаточно пределы в пространстве, чтобы можно было использовать методы исчисления.
Гильбертовы пространства возникают естественно и часто в математика и физика, обычно как бесконечномерный функциональные пространства. Самые ранние гильбертовы пространства были изучены с этой точки зрения в первом десятилетии 20 века. Дэвид Гильберт, Эрхард Шмидт, и Фриджес Рис. Они являются незаменимыми инструментами в теориях уравнения в частных производных, квантовая механика, Анализ Фурье (который включает приложения для обработка сигналов и теплопередача), и эргодическая теория (что составляет математическую основу термодинамика ). Джон фон Нейман ввел термин Гильбертово пространство за абстрактную концепцию, лежащую в основе многих из этих разнообразных приложений. Успех методов гильбертова пространства открыл очень плодотворную эру для функциональный анализ. Помимо классических евклидовых пространств, примеры гильбертовых пространств включают пространства функций, интегрируемых с квадратом, пространства последовательностей, Соболевские пространства состоящий из обобщенные функции, и Пространства Харди из голоморфные функции.
Геометрическая интуиция играет важную роль во многих аспектах теории гильбертова пространства. Точные аналоги теорема Пифагора и закон параллелограмма в гильбертовом пространстве. На более глубоком уровне перпендикулярная проекция на подпространство (аналог "падение высоты "треугольника) играет важную роль в задачах оптимизации и других аспектах теории. Элемент гильбертова пространства может быть однозначно задан его координатами относительно набора оси координат (ан ортонормированный базис ), по аналогии с Декартовы координаты в плоскости. Когда этот набор осей счетно бесконечный, гильбертово пространство также может быть полезно рассматривать в терминах пространства бесконечные последовательности которые суммируемый по квадрату. Последнее пространство часто упоминается в более старой литературе как то Гильбертово пространство. Линейные операторы в гильбертовом пространстве также являются довольно конкретными объектами: в хороших случаях это просто преобразования, которые растягивают пространство на разные факторы во взаимно перпендикулярных направлениях в том смысле, который уточняется изучением их спектр.
Определение и иллюстрация
Мотивирующий пример: евклидово векторное пространство
Одним из наиболее известных примеров гильбертова пространства является Евклидово векторное пространство состоящий из трехмерных векторов, обозначаемый ℝ3, и оснащен скалярное произведение. Скалярное произведение принимает два вектора Икс и у, и производит действительное число Икс · у. Если Икс и у представлены в Декартовы координаты, то скалярное произведение определяется как
Скалярное произведение удовлетворяет свойствам:
- Он симметричен по Икс и у: Икс · у = у · Икс.
- это линейный в первом аргументе: (аИкс1 + бИкс2) · у = аИкс1 · у + бИкс2 · у для любых скаляров а, б, и векторы Икс1, Икс2, и у.
- это положительно определенный: для всех векторов Икс, Икс · Икс ≥ 0 , при равенстве если и только если Икс = 0.
Операция с парами векторов, которая, как и скалярное произведение, удовлетворяет этим трем свойствам, известна как (действительная) внутренний продукт. А векторное пространство оснащенный таким внутренним продуктом, известный как (настоящий) внутреннее пространство продукта. Каждое конечномерное внутреннее пространство продукта также является гильбертовым пространством. Основная особенность скалярного произведения, которая связывает его с евклидовой геометрией, заключается в том, что оно связано как с длиной (или норма ) вектора, обозначаемого ||Икс||, и к углу θ между двумя векторами Икс и у с помощью формулы
Многопараметрическое исчисление в евклидовом пространстве полагается на способность вычислять пределы, и иметь полезные критерии для заключения о существовании ограничений. А математический ряд
состоящий из векторов в ℝ3 является абсолютно сходящийся при условии, что сумма длин сходится как обычный ряд действительных чисел:[1]
Как и в случае с серией скаляров, серия абсолютно сходящихся векторов также сходится к некоторому предельному вектору L в евклидовом пространстве в том смысле, что
Это свойство выражает полнота евклидова пространства: абсолютно сходящийся ряд сходится и в обычном смысле.
Гильбертовы пространства часто берутся за сложные числа. В комплексная плоскость обозначается ℂ снабжен понятием величины, комплексный модуль |z| который определяется как квадратный корень из произведения z с этими комплексно сопряженный:
Если z = Икс + иу является разложением z на действительную и мнимую части, то модуль - это обычная евклидова двумерная длина:
Внутреннее произведение пары комплексных чисел z и ш это продукт z с комплексным сопряжением ш:
Это комплексно. Настоящая часть ⟨z, ш⟩ дает обычные двумерные евклидовы скалярное произведение.
Второй пример - пространство ℂ2 элементы которого являются парами комплексных чисел z = (z1, z2). Тогда внутренний продукт z с другим таким вектором ш = (ш1, ш2) дан кем-то
Настоящая часть ⟨z, ш⟩ тогда является двумерным евклидовым скалярным произведением. Этот внутренний продукт Эрмитский симметричный, что означает, что результат перестановки z и ш является комплексно сопряженным:
Определение
А Гильбертово пространство ЧАС это настоящий или же сложный внутреннее пространство продукта это тоже полное метрическое пространство относительно функции расстояния, индуцированной внутренним произведением.[2]
Чтобы сказать это ЧАС это сложное внутреннее пространство продукта Значит это ЧАС это сложное векторное пространство, на котором есть внутренний продукт ⟨Икс, у⟩ присвоение комплексного числа каждой паре элементов Икс, у из ЧАС который удовлетворяет следующим свойствам:
- Внутренний продукт сопряженно-симметричный; то есть внутренний продукт пары элементов равен комплексно сопряженный внутреннего продукта замененных элементов:
- Внутренний продукт линейный в своем первом[nb 1] аргумент. Для всех комплексных чисел а и б,
- Внутренний продукт элемента с самим собой положительно определенный:
Из свойств 1 и 2 следует, что сложный скалярный продукт сопряженный линейный во втором аргументе, означающем, что
А реальное внутреннее пространство продукта определяется таким же образом, за исключением того, что ЧАС является реальным векторным пространством, а внутренний продукт принимает реальные значения. Такой внутренний продукт будет билинейная карта и (ЧАС, ЧАС, ⟨ ⋅, ⋅⟩) сформирует двойная система.[3]
В норма - вещественная функция
и расстояние d между двумя точками Икс, у в ЧАС определяется в терминах нормы
То, что эта функция является функцией расстояния, означает, во-первых, что она симметрична по Икс и у, во-вторых, расстояние между Икс и сам равен нулю, иначе расстояние между Икс и у должен быть положительным, и, наконец, что неравенство треугольника выполняется, что означает, что длина одного катета треугольника xyz не может превышать сумму длин двух других ног:
Последнее свойство в конечном итоге является следствием более фундаментального Неравенство Коши – Шварца, который утверждает
с равенством тогда и только тогда, когда Икс и у находятся линейно зависимый.
С функцией расстояния, определенной таким образом, любое внутреннее пространство продукта является метрическое пространство, а иногда его называют предгильбертово пространство.[4] Любое предгильбертово пространство, которое также является полный пространство - гильбертово пространство.
В полнота из ЧАС выражается с помощью формы Критерий Коши для последовательностей в ЧАС: предгильбертово пространство ЧАС будет полным, если каждый Последовательность Коши сходится по этой норме элементу в пространстве. Полноту можно охарактеризовать следующим эквивалентным условием: если ряд векторов
сходится абсолютно в том смысле, что
то ряд сходится в ЧАС, в том смысле, что частичные суммы сходятся к элементу ЧАС.
Как полное нормированное пространство, гильбертовы пространства по определению также Банаховы пространства. Как таковые они топологические векторные пространства, в котором топологический такие понятия, как открытость и закрытость подмножеств определены корректно. Особое значение имеет понятие закрытого линейное подпространство гильбертова пространства, которое со скалярным произведением, индуцированным ограничением, также является полным (будучи замкнутым множеством в полном метрическом пространстве) и, следовательно, является гильбертовым пространством само по себе.
Второй пример: пробелы последовательности
В пространство последовательности л2 состоит из всех бесконечные последовательности z = (z1, z2, …) комплексных чисел таких, что серии
сходится. Внутренний продукт на л2 определяется
причем последний ряд сходится вследствие Неравенство Коши – Шварца.
Полнота пространства сохраняется при условии, что всякий раз, когда ряд элементов из л2 сходится абсолютно (по норме), то сходится к элементу из л2. Доказательство основано на математический анализ, и позволяет манипулировать математическими сериями элементов пространства с той же легкостью, что и сериями комплексных чисел (или векторов в конечномерном евклидовом пространстве).[5]
История
До развития гильбертовых пространств были известны другие обобщения евклидовых пространств. математики и физики. В частности, идея абстрактное линейное пространство (векторное пространство) приобрели некоторую популярность к концу 19 века:[6] это пространство, элементы которого можно складывать и умножать на скаляры (например, настоящий или же сложные числа ) без обязательной идентификации этих элементов с "геометрические" векторы, такие как векторы положения и импульса в физических системах. Другие объекты, изучаемые математиками на рубеже ХХ века, в частности пространства последовательности (включая серии ) и пространства функций,[7] естественно рассматривать как линейные пространства. Например, функции можно складывать или умножать на постоянные скаляры, и эти операции подчиняются алгебраическим законам, которым удовлетворяет сложение и скалярное умножение пространственных векторов.
В первом десятилетии 20-го века параллельные разработки привели к введению гильбертовых пространств. Первым из них было наблюдение, возникшее во время Дэвид Гильберт и Эрхард Шмидт исследование интегральные уравнения,[8] эти два интегрируемый с квадратом действительные функции ж и грамм на интервале [а, б] есть внутренний продукт
который обладает многими знакомыми свойствами евклидова скалярного произведения. В частности, идея ортогональный семейство функций имеет значение. Шмидт использовал сходство этого внутреннего продукта с обычным скалярным произведением, чтобы доказать аналог спектральное разложение для оператора вида
куда K - непрерывная функция, симметричная относительно Икс и у. Результирующий разложение по собственным функциям выражает функцию K как серия формы
где функции φп ортогональны в том смысле, что ⟨φпφм⟩ = 0 для всех п ≠ м. Отдельные термины в этой серии иногда называют элементарными решениями продукта. Однако есть разложения по собственным функциям, которые не могут сходиться в подходящем смысле к интегрируемой с квадратом функции: недостающий ингредиент, обеспечивающий сходимость, - это полнота.[9]
Второе развитие было Интеграл Лебега, альтернатива Интеграл Римана представлен Анри Лебег в 1904 г.[10] Интеграл Лебега позволил интегрировать гораздо более широкий класс функций. В 1907 г. Фриджес Рис и Эрнст Сигизмунд Фишер независимо доказали, что пространство L2 квадратных функций, интегрируемых по Лебегу, является полное метрическое пространство.[11] Как следствие взаимодействия между геометрией и полнотой, XIX век является результатом Жозеф Фурье, Фридрих Бессель и Марк-Антуан Парсеваль на тригонометрический ряд легко переносится на эти более общие пространства, в результате чего получается геометрический и аналитический аппарат, обычно известный как Теорема Рисса – Фишера.[12]
Дальнейшие основные результаты были подтверждены в начале 20 века. Например, Теорема Рисса о представлении была независимо создана Морис Фреше и Фриджес Рис в 1907 г.[13] Джон фон Нейман ввел термин абстрактное гильбертово пространство в своей работе над неограниченным Эрмитовы операторы.[14] Хотя другие математики, такие как Герман Вейль и Норберт Винер уже изучив конкретные гильбертовы пространства очень подробно, часто с физически мотивированной точки зрения, фон Нейман дал первое полное и аксиоматическое их рассмотрение.[15] Фон Нейман позже использовал их в своей основополагающей работе по основам квантовой механики,[16] и в его продолжающейся работе с Юджин Вигнер. Название «гильбертово пространство» вскоре было принято другими, например, Германом Вейлем в его книге по квантовой механике и теории групп.[17]
Значение концепции гильбертова пространства было подчеркнуто осознанием того, что оно предлагает одно из лучших математические формулировки квантовой механики.[18] Короче говоря, состояния квантово-механической системы - это векторы в определенном гильбертовом пространстве, наблюдаемые - это эрмитские операторы на этом пространстве симметрии системы унитарные операторы, и измерения находятся ортогональные проекции. Связь между квантово-механическими симметриями и унитарными операторами послужила толчком для развития теории унитарный теория представлений из группы, инициированный в 1928 году работой Германа Вейля.[17] С другой стороны, в начале 1930-х годов стало ясно, что классическая механика может быть описана в терминах гильбертова пространства (Классическая механика Купмана – фон Неймана ) и что некоторые свойства классических динамические системы могут быть проанализированы с использованием техники гильбертова пространства в рамках эргодическая теория.[19]
Алгебра наблюдаемые в квантовой механике, естественно, представляет собой алгебру операторов, определенных в гильбертовом пространстве, согласно Вернер Гейзенберг с матричная механика формулировка квантовой теории. Фон Нейман начал расследование операторные алгебры в 1930-х годах, когда кольца операторов в гильбертовом пространстве. Алгебры, изучаемые фон Нейманом и его современниками, теперь известны как алгебры фон Неймана. В 1940-х годах Израиль Гельфанд, Марк Наймарк и Ирвинг Сигал дал определение разновидности операторных алгебр, названных C * -алгебры это, с одной стороны, не ссылалось на лежащее в основе гильбертово пространство, а с другой - экстраполировало многие полезные свойства операторных алгебр, которые ранее были изучены. В частности, спектральная теорема для самосопряженных операторов, лежащая в основе большей части существующей теории гильбертова пространства, была обобщена на C * -алгебры. Эти методы сейчас являются основными в абстрактном гармоническом анализе и теории представлений.
Примеры
Пространства Лебега
Пространства Лебега функциональные пространства связано с измерять пространства (Икс, M, μ), куда Икс это набор, M это σ-алгебра подмножеств Икс, и μ это счетно-аддитивная мера на M. Позволять L2(Икс, μ) - пространство комплекснозначных измеримых функций на Икс для чего Интеграл Лебега площади абсолютная величина функции конечна, т. е. для функции ж в L2(Икс, μ),
и где функции идентифицируются тогда и только тогда, когда они различаются только набор нулевой меры.
Внутренний продукт функций ж и грамм в L2(Икс, μ) тогда определяется как
- или же
где вторая форма (сопряжение первого элемента) обычно встречается в литературе по теоретической физике. За ж и грамм в L2, интеграл существует из-за неравенства Коши – Шварца и определяет скалярное произведение на пространстве. Оснащен этим внутренним продуктом, L2 на самом деле полный.[20] Интеграл Лебега необходим для обеспечения полноты: например, в областях вещественных чисел недостаточно функций. Интегрируемый по Риману.[21]
Пространства Лебега проявляются во многих естественных условиях. Пространства L2(ℝ) и L2([0,1]) суммируемых с квадратом функций относительно Мера Лебега на действительной прямой и единичном интервале, соответственно, являются естественными областями, на которых можно определить преобразование Фурье и ряд Фурье. В других ситуациях мерой может быть нечто иное, чем обычная мера Лебега на действительной прямой. Например, если ш - любая положительно измеримая функция, пространство всех измеримых функций ж на интервале [0, 1] удовлетворение
называется взвешенный L2 Космос L2
ш([0, 1]), и ш называется весовой функцией. Внутренний продукт определяется
Взвешенное пространство L2
ш([0, 1]) совпадает с гильбертовым пространством L2([0, 1], μ) где мера μ измеримого по Лебегу множества А определяется
Взвешенный L2 Подобные пространства часто используются для изучения ортогональных многочленов, потому что разные семейства ортогональных многочленов ортогональны относительно различных весовых функций.
Соболевские пространства
Соболевские пространства, обозначаемый ЧАСs или же Ws, 2, являются гильбертовыми пространствами. Это особый вид функциональное пространство в котором дифференциация может быть выполнено, но это (в отличие от других Банаховы пространства такой как Пространства Гёльдера ) поддерживают структуру внутреннего продукта. Поскольку дифференцирование разрешено, пространства Соболева представляют собой удобную установку для теории уравнения в частных производных.[22] Они также составляют основу теории прямые методы вариационного исчисления.[23]
За s неотрицательное целое число и Ω ⊂ ℝп, пространство Соболева ЧАСs(Ω) содержит L2 функции, чьи слабые производные порядка до s являются также L2. Внутренний продукт в ЧАСs(Ω) является
где точка указывает скалярное произведение в евклидовом пространстве частных производных каждого порядка. Пространства Соболева также можно определить, когда s не является целым числом.
Пространства Соболева изучаются также с точки зрения спектральной теории, более конкретно опираясь на структуру гильбертова пространства. Если Ω является подходящей областью, то можно определить пространство Соболева ЧАСs(Ω) как пространство Бесселевские потенциалы;[24] грубо,
Здесь Δ является лапласианом и (1 - Δ)−s/2 понимается с точки зрения теорема о спектральном отображении. Помимо рабочего определения пространств Соболева для нецелочисленных s, это определение также имеет особенно желательные свойства в рамках преобразование Фурье что делает его идеальным для изучения псевдодифференциальные операторы. Используя эти методы на компактный Риманово многообразие, можно получить, например, Разложение Ходжа, что является основой Теория Ходжа.[25]
Пространства голоморфных функций
Пространства Харди
В Пространства Харди - функциональные пространства, возникающие в комплексный анализ и гармонический анализ, элементы которого определены голоморфные функции в сложной области.[26] Позволять U обозначить единичный диск в комплексной плоскости. Тогда пространство Харди ЧАС2(U) определяется как пространство голоморфных функций ж на U так что средства
оставаться ограниченным для р < 1. Норма на этом пространстве Харди определяется формулой
Пространства Харди в круге связаны с рядами Фурье. Функция ж в ЧАС2(U) если и только если
куда
Таким образом ЧАС2(U) состоит из тех функций, которые L2 на окружности, отрицательные частотные коэффициенты Фурье которой равны нулю.
Пространства Бергмана
В Пространства Бергмана - еще одно семейство гильбертовых пространств голоморфных функций.[27] Позволять D - ограниченное открытое множество в комплексная плоскость (или многомерное сложное пространство) и пусть L2, час(D) - пространство голоморфных функций ж в D которые также находятся в L2(D) в том смысле, что
где интеграл берется по мере Лебега в D. Четко L2, час(D) является подпространством L2(D); на самом деле это закрыто подпространство, и, следовательно, гильбертово пространство само по себе. Это следствие оценки, действующей на компактный подмножества K из D, который
что, в свою очередь, следует из Интегральная формула Коши. Таким образом, сходимость последовательности голоморфных функций в L2(D) подразумевает также компактная сходимость, а значит, и предельная функция голоморфна. Еще одно следствие этого неравенства состоит в том, что линейный функционал, вычисляющий функцию ж в точке D на самом деле продолжается L2, час(D). Теорема Рисса о представлении подразумевает, что оценочный функционал может быть представлен как элемент L2, час(D). Таким образом, для каждого z ∈ D, есть функция ηz ∈ L2, час(D) такой, что
для всех ж ∈ L2, час(D). Подынтегральное выражение
известен как Ядро Бергмана из D. Этот интегральное ядро удовлетворяет воспроизводящему свойству
Пространство Бергмана является примером воспроизводящее ядро гильбертова пространства, которое является гильбертовым пространством функций вместе с ядром K(ζ, z) который проверяет воспроизводящее свойство, аналогичное этому. Пространство Харди ЧАС2(D) также допускает воспроизводящее ядро, известное как Ядро сегу.[28] Воспроизводящие ядра распространены и в других областях математики. Например, в гармонический анализ то Ядро Пуассона является воспроизводящим ядром гильбертова пространства квадратично интегрируемых гармонические функции в единичный мяч. То, что последнее вообще является гильбертовым пространством, является следствием теоремы о среднем значении для гармонических функций.
Приложения
Многие приложения гильбертовых пространств используют тот факт, что гильбертовы пространства поддерживают обобщения простых геометрических понятий, таких как проекция и изменение основы из их обычных конечномерных условий. В частности, спектральная теория из непрерывный самосопряженный линейные операторы на гильбертовом пространстве обобщает обычные спектральное разложение из матрица, и это часто играет важную роль в приложениях теории к другим областям математики и физики.
Теория Штурма – Лиувилля

В теории обыкновенные дифференциальные уравнения спектральные методы на подходящем гильбертовом пространстве используются для изучения поведения собственных значений и собственных функций дифференциальных уравнений. Например, Проблема Штурма – Лиувилля. возникает при изучении гармоник волн в струне скрипки или барабане и является центральной проблемой в обыкновенные дифференциальные уравнения.[29] Задача представляет собой дифференциальное уравнение вида
для неизвестной функции у на интервале [а, б], удовлетворяющие общему однородному Граничные условия Робина
Функции п, q, и ш заданы заранее, и задача состоит в том, чтобы найти функцию у и константы λ для которого уравнение имеет решение. Проблема имеет решения только для определенных значений λ, называемые собственными значениями системы, и это следствие спектральной теоремы для компактные операторы применяется к интегральный оператор определяется Функция Грина для системы. Кроме того, еще одним следствием этого общего результата является то, что собственные значения λ системы можно расположить в возрастающей последовательности, стремящейся к бесконечности.[nb 2]
Уравнения с частными производными
Гильбертовы пространства образуют основной инструмент при изучении уравнения в частных производных.[22] Для многих классов дифференциальных уравнений в частных производных, таких как линейные эллиптические уравнения, можно рассматривать обобщенное решение (известное как слабый решение) за счет расширения класса функций. Многие слабые формулировки включают класс Соболевские функции, которое является гильбертовым пространством. Подходящая слабая формулировка сводит к геометрической проблеме аналитическую задачу поиска решения или, что более важно, демонстрации того, что решение существует и уникально для данных граничных данных. Для линейных эллиптических уравнений одним геометрическим результатом, обеспечивающим однозначную разрешимость большого класса задач, является Теорема Лакса – Милграма. Эта стратегия формирует рудимент Метод Галеркина (а метод конечных элементов ) для численного решения уравнений в частных производных.[30]
Типичным примером является Уравнение Пуассона −Δты = грамм с Граничные условия Дирихле в ограниченной области Ω в ℝ2. Слабая формулировка состоит в нахождении функции ты такое, что для всех непрерывно дифференцируемых функций v в Ω исчезающий на границе:
Это может быть преобразовано в терминах гильбертова пространства ЧАС1
0(Ω) состоящий из функций ты такой, что тывместе со своими слабыми частными производными интегрируемы с квадратом на Ω, и обращаются в нуль на границе. Тогда вопрос сводится к поиску ты в этом пространстве, что для всех v в этом пространстве
куда а является непрерывным билинейная форма, и б является непрерывным линейный функционал, задаваемые соответственно
Поскольку уравнение Пуассона имеет вид эллиптический, из неравенства Пуанкаре следует, что билинейная форма а является принудительный. Тогда теорема Лакса – Милграма гарантирует существование и единственность решений этого уравнения.
Гильбертовы пространства позволяют аналогичным образом формулировать многие эллиптические уравнения в частных производных, и теорема Лакса – Мильграма становится основным инструментом их анализа. С соответствующими модификациями аналогичные методы могут быть применены к параболические уравнения в частных производных и некоторые гиперболические уравнения в частных производных.
Эргодическая теория

Поле эргодическая теория изучение долгосрочного поведения хаотичный динамические системы. Типичный случай поля, к которому применяется эргодическая теория, - это термодинамика, в котором - хотя микроскопическое состояние системы чрезвычайно сложно (невозможно понять ансамбль индивидуальных столкновений между частицами материи) - среднее поведение на достаточно длительных временных интервалах поддается контролю. В законы термодинамики утверждения о таком среднем поведении. В частности, одна формулировка нулевой закон термодинамики утверждает, что в течение достаточно длительного времени единственным функционально независимым измерением термодинамической системы в состоянии равновесия является ее полная энергия в виде температура.
Эргодическая динамическая система - это система, для которой, помимо энергии, измеряемой Гамильтониан - других функционально независимых сохраненные количества на фазовое пространство. Более явно, предположим, что энергия E фиксировано, и пусть ΩE - подмножество фазового пространства, состоящее из всех состояний энергии E (энергетическая поверхность), и пусть Тт обозначим оператор эволюции на фазовом пространстве. Динамическая система является эргодической, если на ней нет непрерывных непостоянных функций. ΩE такой, что
для всех ш на ΩE и все время т. Теорема Лиувилля означает, что существует мера μ на энергетической поверхности, инвариантной относительно перевод времени. В результате перевод времени - это унитарное преобразование гильбертова пространства L2(ΩE, μ) состоящий из квадратично интегрируемых функций на энергетической поверхности ΩE относительно внутреннего продукта
Эргодическая теорема фон Неймана о среднем[19] заявляет следующее:
- Если Uт является (сильно непрерывной) однопараметрической полугруппой унитарных операторов в гильбертовом пространстве ЧАС, и п ортогональная проекция на пространство общих неподвижных точек Uт, {Икс ∈ЧАС | UтИкс = Икс, ∀т > 0}, тогда
Для эргодической системы фиксированный набор временной эволюции состоит только из постоянных функций, поэтому из эргодической теоремы следует следующее:[31] для любой функции ж ∈ L2(ΩE, μ),
То есть долгое среднее значение наблюдаемого ж равна своему математическому ожиданию над поверхностью энергии.
Анализ Фурье
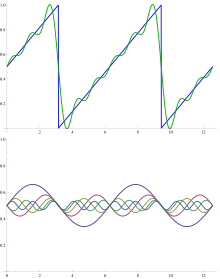

Одна из основных целей Анализ Фурье состоит в том, чтобы разложить функцию на (возможно, бесконечное) линейная комбинация заданных базисных функций: связанные Ряд Фурье. Классический ряд Фурье, связанный с функцией ж определенный на интервале [0, 1] представляет собой серию вида
куда
Пример сложения первых нескольких членов ряда Фурье для пилообразной функции показан на рисунке. Базисные функции - это синусоидальные волны с длинами волн λ/п (для целого п) короче длины волны λ самой пилы (кроме п = 1, то фундаментальный волна). Все базовые функции имеют узлы в узлах пилообразной формы, но все, кроме основных, имеют дополнительные узлы. Колебание суммированных членов вокруг пилообразной части называется колебанием Феномен Гиббса.
Существенная проблема классических рядов Фурье состоит в том, чтобы понять, в каком смысле ряд Фурье сходится, если вообще сходится, к функции ж. Один из возможных ответов на этот вопрос дают методы гильбертова пространства.[32] Функции еп(θ) = е2πinθ образуют ортогональный базис гильбертова пространства L2([0, 1]). Следовательно, любую интегрируемую с квадратом функцию можно представить в виде ряда
и, более того, этот ряд сходится в смысле гильбертова пространства (т.е. L2 иметь в виду ).
Проблема также может быть изучена с абстрактной точки зрения: каждое гильбертово пространство имеет ортонормированный базис, и каждый элемент гильбертова пространства может быть записан уникальным способом как сумма, кратная этим базисным элементам. Коэффициенты, возникающие на этих базисных элементах, иногда абстрактно называют коэффициентами Фурье элемента пространства.[33] Абстракция особенно полезна, когда более естественно использовать разные базовые функции для пространства, например L2([0, 1]). Во многих случаях желательно не разбивать функцию на тригонометрические функции, а, скорее, на ортогональные многочлены или же вейвлеты например,[34] и в более высоких измерениях в сферические гармоники.[35]
Например, если еп - любые ортонормированные базисные функции L2[0, 1], то заданная функция в L2[0, 1] можно аппроксимировать как конечную линейную комбинацию[36]
Коэффициенты {аj} выбраны, чтобы иметь значение ||ж − жп||2 как можно меньше. Геометрически наилучшее приближение это ортогональная проекция из ж на подпространство, состоящее из всех линейных комбинаций {еj}, и может быть рассчитан[37]
Эта формула минимизирует разницу ||ж − жп||2 является следствием Неравенство Бесселя и формула Парсеваля.
В различных приложениях к физическим задачам функцию можно разложить на физически значимые собственные функции из дифференциальный оператор (обычно Оператор Лапласа ): это формирует основу для спектрального исследования функций со ссылкой на спектр дифференциального оператора.[38] Конкретное физическое приложение связано с проблемой слышать форму барабана: учитывая основные виды вибрации, которые может вызывать пластина барабана, можно ли сделать вывод о форме самого барабана?[39] Математическая постановка этого вопроса включает в себя Собственные значения Дирихле уравнения Лапласа на плоскости, которые представляют основные моды колебаний в прямой аналогии с целыми числами, которые представляют основные моды колебаний струны скрипки.
Спектральная теория также лежит в основе некоторых аспектов преобразование Фурье функции. В то время как анализ Фурье разлагает функцию, определенную на компактный набор в дискретный спектр лапласиана (который соответствует колебаниям струны скрипки или барабана), преобразование Фурье функции - это разложение функции, определенной на всем евклидовом пространстве, на ее компоненты в непрерывный спектр лапласиана. Преобразование Фурье также является геометрическим, в некотором смысле точным с помощью Теорема Планшереля, который утверждает, что это изометрия одного гильбертова пространства («временная область») с другим («частотная область»). Это свойство изометрии преобразования Фурье является повторяющейся темой в абстрактных гармонический анализ, о чем свидетельствует, например, Теорема Планшереля для сферических функций происходящий в некоммутативный гармонический анализ.
Квантовая механика

В математически строгой формулировке квантовая механика, разработан Джон фон Нейман,[40] возможные состояния (точнее, чистые состояния ) квантово-механической системы представлены единичные векторы (называется векторы состояния), находящиеся в сложном сепарабельном гильбертовом пространстве, известном как пространство состояний, корректно определенные с точностью до комплексного числа нормы 1 ( фазовый фактор ). Другими словами, возможные состояния - это точки в проективизация гильбертова пространства, обычно называемого сложное проективное пространство. Точная природа этого гильбертова пространства зависит от системы; например, состояния положения и импульса для одиночной нерелятивистской частицы с нулевым спином - это пространство всех интегрируемый с квадратом функций, а состояния для спина одиночного протона являются единичными элементами двумерного комплексного гильбертова пространства спиноры. Каждая наблюдаемая представлена самосопряженный линейный оператор действуя в пространстве состояний. Каждому собственному состоянию наблюдаемой соответствует собственный вектор оператора, и связанный собственное значение соответствует значению наблюдаемого в этом собственном состоянии.
Внутренний продукт между двумя векторами состояния - это комплексное число, известное как амплитуда вероятности. Во время идеального измерения квантово-механической системы вероятность того, что система коллапсирует из заданного начального состояния в конкретное собственное состояние, дается квадратом абсолютная величина амплитуд вероятностей между начальным и конечным состояниями. Возможными результатами измерения являются собственные значения оператора, что объясняет выбор самосопряженных операторов, поскольку все собственные значения должны быть действительными. Распределение вероятностей наблюдаемого в данном состоянии можно найти, вычислив спектральное разложение соответствующего оператора.
Для общей системы состояния обычно не являются чистыми, но вместо этого представлены как статистические смеси чистых состояний или смешанных состояний, заданных формулой матрицы плотности: самосопряженные операторы след один в гильбертовом пространстве. Более того, для общих квантово-механических систем эффекты одного измерения могут влиять на другие части системы способом, который описывается положительная операторнозначная мера. Таким образом, структура как состояний, так и наблюдаемых в общей теории значительно сложнее, чем идеализация для чистых состояний.
Восприятие цвета
Любой настоящий физический цвет может быть представлен комбинацией чистых спектральные цвета. Поскольку физические цвета могут состоять из любого количества спектральных цветов, пространство физических цветов может быть точно представлено гильбертовым пространством над спектральными цветами. У людей есть три типа колбочек для восприятия цвета, поэтому воспринимаемые цвета могут быть представлены в трехмерном евклидовом пространстве. Линейное отображение `` многие к одному '' из гильбертова пространства физических цветов в евклидово пространство воспринимаемых человеком цветов объясняет, почему многие различные физические цвета могут восприниматься людьми как идентичные (например, чистый желтый свет по сравнению с сочетанием красного и зеленого свет, смотри метамерия ).
Характеристики
Пифагорейская идентичность
Два вектора ты и v в гильбертовом пространстве ЧАС ортогональны, когда ⟨ты, v⟩ = 0. Обозначения для этого: ты ⊥ v. В более общем плане, когда S это подмножество в ЧАС, обозначение ты ⊥ S Значит это ты ортогонален каждому элементу из S.
Когда ты и v ортогональны,
Индукцией по п, это распространяется на любую семью ты1, …, тып из п ортогональные векторы,
В то время как заявленная пифагорейская идентичность действительна в любом внутреннем пространстве продукта, полнота требуется для расширения пифагорейской идентичности на ряды. Серия ∑тыk из ортогональный векторов сходится в ЧАС тогда и только тогда, когда ряд квадратов норм сходится, и
Кроме того, сумма ряда ортогональных векторов не зависит от порядка, в котором она берется.
Идентичность и поляризация параллелограмма

По определению каждое гильбертово пространство также является Банахово пространство. Кроме того, в каждом гильбертовом пространстве следующие тождество параллелограмма держит:
И наоборот, каждое банахово пространство, в котором выполняется тождество параллелограмма, является гильбертовым пространством, а скалярное произведение однозначно определяется нормой поляризационная идентичность.[41] Для реальных гильбертовых пространств поляризационное тождество имеет вид
Для комплексных гильбертовых пространств это
Из закона параллелограмма следует, что любое гильбертово пространство является равномерно выпуклое банахово пространство.[42]
Наилучшее приближение
В этом подразделе используются Теорема проекции Гильберта. Если C непустое замкнутое выпуклое подмножество гильбертова пространства ЧАС и Икс точка в ЧАС, существует единственная точка у ∈ C что минимизирует расстояние между Икс и указывает на C,[43]
Это равносильно утверждению, что в сдвинутом выпуклом множестве есть точка с минимальной нормой D = C − Икс. Доказательство состоит в том, чтобы показать, что каждая минимизирующая последовательность (dп) ⊂ D является Коши (используя тождество параллелограмма), следовательно, сходится (используя полноту) к точке в D имеющий минимальную норму. Вообще говоря, это верно в любом равномерно выпуклом банаховом пространстве.[44]
Когда этот результат применяется к замкнутому подпространству F из ЧАС, можно показать, что точка у ∈ F ближайший к Икс характеризуется[45]
Эта точка у это ортогональная проекция из Икс на F, а отображение пF : Икс → у линейна (см. Ортогональные дополнения и проекции ). Этот результат особенно важен в Прикладная математика, особенно числовой анализ, где он составляет основу наименьших квадратов методы.[46]
В частности, когда F не равно ЧАС, можно найти ненулевой вектор v ортогонален F (Выбрать Икс ∉ F и v = Икс − у). Очень полезный критерий получается применением этого наблюдения к замкнутому подпространству F генерируется подмножеством S из ЧАС.
- Подмножество S из ЧАС охватывает плотное векторное подпространство, если (и только если) вектор 0 является единственным вектором v ∈ ЧАС ортогонален S.
Двойственность
В двойное пространство ЧАС* это пространство всего непрерывный линейные функции из пространства ЧАС в базовое поле. Он несет естественную норму, определяемую
Эта норма удовлетворяет закон параллелограмма, и поэтому двойное пространство также является внутренним пространством продукта, где этот внутренний продукт может быть определен в терминах этой двойственной нормы с помощью поляризационная идентичность. Двойственное пространство также полно, поэтому оно является гильбертовым пространством само по себе. Если е• = (ея)я ∈ я является полным ортонормированным базисом для ЧАС тогда внутренний продукт на двойственном пространстве любых двух является
где все члены этого ряда, кроме счетного, равны нулю.
В Теорема Рисса о представлении дает удобное описание двойственного пространства. Каждому элементу ты из ЧАС, есть уникальный элемент φты из ЧАС*, определяется
где, кроме того,
Теорема Рисса о представлении утверждает, что отображение из ЧАС к ЧАС* определяется ты ↦ φты является сюръективный, что делает эту карту изометрический антилинейный изоморфизм.[47] Итак, к каждому элементу φ двойного ЧАС* существует один и только один тыφ в ЧАС такой, что
для всех Икс ∈ ЧАС. Внутренний продукт на двойном пространстве ЧАС* удовлетворяет
Изменение порядка в правой части восстанавливает линейность в φ из антилинейности тыφ. В реальном случае антилинейный изоморфизм от ЧАС к его двойственному на самом деле является изоморфизмом, и поэтому вещественные гильбертовые пространства естественно изоморфны своим собственным двойственным.
Представляющий вектор тыφ получается следующим образом. Когда φ ≠ 0, то ядро F = Ker (φ) замкнутое векторное подпространство ЧАС, не равно ЧАС, значит, существует ненулевой вектор v ортогонален F. Вектор ты является подходящим скалярным кратным λv из v. Требование, чтобы φ(v) = ⟨v, ты⟩ дает
Эта переписка φ ↔ ты эксплуатируется обозначение бюстгальтера популярен в физика. В физике принято считать, что внутренний продукт, обозначаемый ⟨Икс|у⟩, линейна справа,
Результат ⟨Икс|у⟩ можно рассматривать как действие линейного функционала ⟨Икс| (в бюстгальтер) на векторе |у⟩ (в кет).
Теорема Рисса о представлении основывается не только на наличии внутреннего продукта, но и на полноте пространства. Фактически из теоремы следует, что топологический двойственный любого внутреннего пространства продукта можно идентифицировать с его завершением. Непосредственным следствием теоремы Рисса о представлении также является то, что гильбертово пространство ЧАС является рефлексивный, что означает, что естественная карта из ЧАС в его двойное двойное пространство является изоморфизмом.
Слабо сходящиеся последовательности
В гильбертовом пространстве ЧАС, последовательность {Иксп} является слабо сходящийся к вектору Икс ∈ ЧАС когда
для каждого v ∈ ЧАС.
Например, любая ортонормированная последовательность {жп} слабо сходится к 0, как следствие Неравенство Бесселя. Каждая слабо сходящаяся последовательность {Иксп} ограничен принцип равномерной ограниченности.
Наоборот, любая ограниченная последовательность в гильбертовом пространстве допускает слабо сходящиеся подпоследовательности (Теорема Алаоглу ).[48] Этот факт может быть использован для доказательства результатов минимизации непрерывных выпуклые функционалы, так же, как Теорема Больцано – Вейерштрасса используется для непрерывных функций на ℝd. Среди нескольких вариантов одно простое утверждение выглядит следующим образом:[49]
- Если ж : ЧАС → ℝ выпуклая непрерывная функция такая, что ж(Икс) как правило +∞ когда ||Икс|| как правило ∞, тогда ж допускает минимум в какой-то момент Икс0 ∈ ЧАС.
Этот факт (и его различные обобщения) являются фундаментальными для прямые методы в вариационное исчисление. Результаты минимизации выпуклых функционалов также являются прямым следствием немного более абстрактного факта, что замкнутые ограниченные выпуклые подмножества в гильбертовом пространстве ЧАС находятся слабо компактный, поскольку ЧАС рефлексивно. Существование слабо сходящихся подпоследовательностей является частным случаем Теорема Эберлейна – Шмулиана.
Свойства банахова пространства
Любая общая собственность Банаховы пространства продолжает выполняться для гильбертовых пространств. В теорема об открытом отображении заявляет, что непрерывный сюръективный линейное преобразование из одного банахова пространства в другое - это открытое отображение Это означает, что он отправляет открытые наборы в открытые наборы. Следствием является ограниченная обратная теорема, что непрерывный и биективный линейная функция из одного банахова пространства в другое является изоморфизмом (т. е. непрерывным линейным отображением, обратное к которому также непрерывно). Эту теорему значительно проще доказать в случае гильбертовых пространств, чем в общих банаховых пространствах.[50] Теорема об открытом отображении эквивалентна теореме теорема о замкнутом графике, который утверждает, что линейная функция из одного банахова пространства в другое непрерывна тогда и только тогда, когда ее график является закрытый набор.[51] В случае гильбертовых пространств это основа при изучении неограниченные операторы (видеть закрытый оператор ).
(Геометрический) Теорема Хана – Банаха утверждает, что замкнутое выпуклое множество можно отделить от любой точки вне его с помощью гиперплоскость гильбертова пространства. Это непосредственное следствие наилучшее приближение свойство: если у является элементом замкнутого выпуклого множества F ближайший к Икс, то разделяющая гиперплоскость - это плоскость, перпендикулярная отрезку ху проходя через его середину.[52]
Операторы в гильбертовых пространствах
Ограниченные операторы
В непрерывный линейные операторы А : ЧАС1 → ЧАС2 из гильбертова пространства ЧАС1 во второе гильбертово пространство ЧАС2 находятся ограниченный в том смысле, что они отображают ограниченные множества ограниченным множествам. Наоборот, если оператор ограничен, то он непрерывен. Пространство таких ограниченные линейные операторы имеет норма, то норма оператора данный
Сумма и композиция двух ограниченных линейных операторов снова ограничены и линейны. За у в ЧАС2, карта, которая отправляет Икс ∈ ЧАС1 к ⟨Топор, у⟩ линейно и непрерывно, и согласно Теорема Рисса о представлении поэтому можно представить в виде
для какого-то вектора А*у в ЧАС1. Это определяет еще один ограниченный линейный оператор А* : ЧАС2 → ЧАС1, то прилегающий из А. Сопряженный удовлетворяет А** = А. Когда теорема о представлении Рисса используется для отождествления каждого гильбертова пространства с его непрерывным сопряженным пространством, сопряженное к А можно показать как идентично то транспонировать тА : ЧАС2* → ЧАС1* из А, который по определению отправляет к функциональному
Набор B (ЧАС) всех линейных ограниченных операторов на ЧАС (имеется в виду операторы ЧАС → ЧАС) вместе с операциями сложения и композиции, нормой и сопряженной операцией является C * -алгебра, который является разновидностью операторная алгебра.
Элемент А из B (ЧАС) называется самосопряженным или эрмитовым, если А* = А. Если А эрмитский и ⟨Топор, Икс⟩ ≥ 0 для каждого Икс, тогда А называется неотрицательным, пишется А ≥ 0; если равенство выполняется только тогда, когда Икс = 0, тогда А называется «положительным». Множество самосопряженных операторов допускает частичный заказ, в котором А ≥ B если А − B ≥ 0. Если А имеет форму B*B для некоторых B, тогда А неотрицательно; если B обратима, то А положительный. Обратное также верно в том смысле, что для неотрицательного оператора Асуществует единственная неотрицательная квадратный корень B такой, что
В некотором смысле, уточненном спектральная теорема, самосопряженные операторы можно рассматривать как «реальные» операторы. Элемент А из B (ЧАС) называется нормальный если А*А = AA*. Нормальные операторы разлагаются на сумму самосопряженных операторов и мнимую кратную самосопряженного оператора
которые ездят друг с другом. Нормальные операторы также можно рассматривать с точки зрения их действительной и мнимой частей.
Элемент U из B (ЧАС) называется унитарный если U обратим, а его обратный U*. Это также можно выразить, потребовав, чтобы U быть на и ⟨Ux, Уй⟩ = ⟨Икс, у⟩ для всех Икс, у ∈ ЧАС. Унитарные операторы образуют группа под составом, который является группа изометрии из ЧАС.
Элемент B (ЧАС) является компактный если он отправляет ограниченные множества в относительно компактный наборы. Эквивалентно ограниченный оператор Т компактно, если для любой ограниченной последовательности {Иксk}, последовательность {Txk} имеет сходящуюся подпоследовательность. Много интегральные операторы компактны и фактически определяют специальный класс операторов, известный как Операторы Гильберта – Шмидта которые особенно важны при изучении интегральные уравнения. Фредгольмовы операторы отличаются от компактного оператора кратным единице и эквивалентно характеризуются как операторы с конечномерным ядро и коядро. Индекс фредгольмова оператора Т определяется
Индекс гомотопия инвариантен и играет важную роль в дифференциальная геометрия через Теорема Атьи – Зингера об индексе.
Неограниченные операторы
Неограниченные операторы также поддаются трактовке в гильбертовых пространствах и имеют важные приложения к квантовая механика.[53] Неограниченный оператор Т в гильбертовом пространстве ЧАС определяется как линейный оператор, область определения D(Т) является линейным подпространством в ЧАС. Часто домен D(Т) является плотным подпространством в ЧАС, в таком случае Т известен как плотно определенный оператор.
Сопряженный к плотно определенному неограниченному оператору определяется по существу так же, как и для ограниченных операторов. Самосопряженные неограниченные операторы играть роль наблюдаемые в математической формулировке квантовой механики. Примеры самосопряженных неограниченных операторов в гильбертовом пространстве L2(ℝ) находятся:[54]
- Подходящее расширение дифференциального оператора
- Умножение наИкс оператор:
Они соответствуют импульс и позиция наблюдаемые соответственно. Обратите внимание, что ни А ни B определяется на всех ЧАС, поскольку в случае А производная может не существовать, а в случае B функция произведения не обязательно должна быть квадратично интегрируемой. В обоих случаях множество возможных аргументов образуют плотные подпространства L2(ℝ).
Конструкции
Прямые суммы
Два гильбертовых пространства ЧАС1 и ЧАС2 можно объединить в другое гильбертово пространство, называемое (ортогональная) прямая сумма,[55] и обозначен
состоящий из множества всех заказанные пары (Икс1, Икс2) куда Икся ∈ ЧАСя, я = 1, 2, и внутренний продукт, определяемый
В более общем смысле, если ЧАСя семейство гильбертовых пространств, индексируемое я ∈ я, то прямая сумма ЧАСя, обозначенный
состоит из множества всех индексированных семейств
в Декартово произведение из ЧАСя такой, что
Внутренний продукт определяется
Каждый из ЧАСя входит как замкнутое подпространство в прямую сумму всех ЧАСя. Более того, ЧАСя попарно ортогональны. Наоборот, если существует система замкнутых подпространств, Vя, я ∈ я, в гильбертовом пространстве ЧАС, которые попарно ортогональны и объединение плотно в ЧАС, тогда ЧАС канонически изоморфна прямой сумме Vя. В этом случае, ЧАС называется внутренней прямой суммой Vя. Прямая сумма (внутренняя или внешняя) также оснащена семейством ортогональных проекций. Eя на яое прямое слагаемое ЧАСя. Эти проекции ограничены, самосопряжены, идемпотент операторы, удовлетворяющие условию ортогональности
В спектральная теорема за компактный самосопряженные операторы в гильбертовом пространстве ЧАС утверждает, что ЧАС разбивается на ортогональную прямую сумму собственных подпространств оператора, а также дает явное разложение оператора как сумму проекций на собственные подпространства. Прямая сумма гильбертовых пространств также появляется в квантовой механике как Пространство фока системы, содержащей переменное число частиц, где каждое гильбертово пространство в прямой сумме соответствует дополнительному степень свободы для квантово-механической системы. В теория представлений, то Теорема Питера – Вейля гарантирует, что любой унитарное представительство из компактная группа на гильбертовом пространстве распадается как прямая сумма конечномерных представлений.
Тензорные продукты
Если Икс1, у1 ∊ ЧАС1 и Икс2, у2 ∊ ЧАС2, затем определяется внутренний продукт на (обычном) тензорное произведение следующее. На простые тензоры, позволять
Затем эта формула расширяется на полуторалинейность к внутреннему продукту на ЧАС1 ⊗ ЧАС2. Гильбертово тензорное произведение ЧАС1 и ЧАС2, иногда обозначается ЧАС1 ЧАС2, - гильбертово пространство, полученное пополнением ЧАС1 ⊗ ЧАС2 для показателя, связанного с этим внутренним продуктом.[56]
Примером может служить гильбертово пространство L2([0, 1]). Гильбертово тензорное произведение двух копий L2([0, 1]) изометрически и линейно изоморфно пространству L2([0, 1]2) квадратично интегрируемых функций на квадрате [0, 1]2. Этот изоморфизм посылает простой тензор ж1 ⊗ ж2 к функции
на пл.
Этот пример типичен в следующем смысле.[57] Связано с каждым простым тензорным произведением Икс1 ⊗ Икс2 оператор ранга один из ЧАС∗
1 к ЧАС2 который отображает данный Икс* ∈ ЧАС∗
1 в качестве
Это отображение, определенное на простых тензорах, продолжается до линейной идентификации между ЧАС1 ⊗ ЧАС2 и пространство операторов конечного ранга из ЧАС∗
1 к ЧАС2. Это распространяется на линейную изометрию гильбертова тензорного произведения ЧАС1 ЧАС2 с гильбертовым пространством HS(ЧАС∗
1, ЧАС2) из Операторы Гильберта – Шмидта из ЧАС∗
1 к ЧАС2.
Ортонормированные базы
Понятие ортонормированный базис из линейной алгебры обобщается на случай гильбертовых пространств.[58] В гильбертовом пространстве ЧАС, ортонормированный базис - это семейство {еk}k ∈ B элементов ЧАС удовлетворяющие условиям:
- Ортогональность: Каждые два разных элемента B ортогональны: ⟨еk, еj⟩ = 0 для всех k, j ∈ B с k ≠ j.
- Нормализация: Каждый элемент семейства имеет норму 1: ||еk|| = 1 для всех k ∈ B.
- Полнота: The линейный пролет семьи еk, k ∈ B, является плотный в ЧАС.
Система векторов, удовлетворяющая первым двум условиям базиса, называется ортонормированной системой или ортонормированным множеством (или ортонормированной последовательностью, если B является счетный ). Такая система всегда линейно независимый. Полноту ортонормированной системы векторов гильбертова пространства можно эквивалентно переформулировать как:
- если ⟨v, еk⟩ = 0 для всех k ∈ B и немного v ∈ ЧАС тогда v = 0.
Это связано с тем, что единственным вектором, ортогональным плотному линейному подпространству, является нулевой вектор, так как если S - любое ортонормированное множество и v ортогонален S, тогда v ортогонален замыканию линейной оболочки S, то есть все пространство.
Примеры ортонормированных баз включают:
- набор {(1, 0, 0), (0, 1, 0), (0, 0, 1)} образует ортонормированную основу ℝ3 с скалярное произведение;
- последовательность {жп : п ∈ ℤ} с жп(Икс) = exp (2πинкс) образует ортонормированный базис сложного пространства L2([0, 1]);
В бесконечномерном случае ортонормированный базис не будет базисом в смысле линейная алгебра; чтобы различать эти два, последний базис также называется Основа Гамеля. То, что промежуток базисных векторов является плотным, означает, что каждый вектор в пространстве может быть записан как сумма бесконечного ряда, а ортогональность означает, что это разложение уникально.
Пространства последовательности
Космос суммируемых с квадратом последовательностей комплексных чисел - это множество бесконечных последовательностей
действительных или комплексных чисел, таких что
Это пространство имеет ортонормированную основу:
Это пространство является бесконечномерным обобщением пространство конечномерных векторов. Обычно это первый пример, показывающий, что в бесконечномерных пространствах множество закрыто и ограниченный не обязательно (последовательно) компактный (как и во всех конечный размерные пространства). В самом деле, набор ортонормированных векторов, приведенный выше, показывает это: это бесконечная последовательность векторов в единичном шаре (т. Е. Шаре точек с нормой, меньшей или равной единице). Это множество, очевидно, ограничено и замкнуто; однако никакая подпоследовательность этих векторов не сходится ни к чему, и, следовательно, единичный шар в не компактный. Интуитивно это происходит потому, что «всегда есть другое направление координат», в которое могут уклоняться следующие элементы последовательности.
Можно обобщить пространство во многих отношениях. Например, если B - любое (бесконечное) множество, то можно сформировать гильбертово пространство последовательностей с индексным множеством B, определяется
Суммирование по B здесь определяется
то супремум берется по всем конечным подмножествамB. Отсюда следует, что для того, чтобы эта сумма была конечной, каждый элемент л2(B) имеет только счетное количество ненулевых членов. Это пространство становится гильбертовым пространством со скалярным произведением
для всех Икс, у ∈ л2(B). Здесь также имеется счетное число ненулевых членов и она безусловно сходится согласно неравенству Коши – Шварца.
Ортонормированный базис л2(B) индексируется набором B, данный
Неравенство Бесселя и формула Парсеваля
Позволять ж1, ..., жп - конечная ортонормированная система вЧАС. Для произвольного вектора Икс ∈ ЧАС, позволять
потом ⟨Икс, жk⟩ = ⟨у, жk⟩ для каждого k = 1, …, п. Следует, что Икс − у ортогонален каждому жk, следовательно Икс − у ортогоналену. Дважды используя тождество Пифагора, следует, что
Позволять {жя}, я ∈ я, - произвольная ортонормированная система вЧАС. Применяя предыдущее неравенство к каждому конечному подмножеству J из я дает неравенство Бесселя:[59]
(согласно определению сумма произвольной семьи неотрицательных действительных чисел).
Геометрически из неравенства Бесселя следует, что ортогональная проекция Икс на линейное подпространство, натянутое на жя имеет норму, не превышающую норму Икс. В двух измерениях это утверждение, что длина катета прямоугольного треугольника не может превышать длину гипотенузы.
Неравенство Бесселя - это ступенька к более сильному результату, называемому Личность Парсеваля, который определяет случай, когда неравенство Бесселя фактически является равенством. По определению, если {еk}k ∈ B является ортонормированным базисом ЧАС, то каждый элемент Икс из ЧАС можно записать как
Даже если B несчетно, неравенство Бесселя гарантирует, что выражение хорошо определено и состоит только из счетного числа ненулевых членов. Эта сумма называется разложением Фурье Икс, а отдельные коэффициенты ⟨Икс, еk⟩ коэффициенты Фурье Икс. Личность Парсеваля затем утверждает, что
Наоборот, если {еk} является ортонормированным множеством, так что тождество Парсеваля выполняется для каждого Икс, тогда {еk} является ортонормированным базисом.
Размерность Гильберта
Как следствие Лемма Цорна, каждый Гильбертово пространство допускает ортонормированный базис; кроме того, любые два ортонормированных базиса одного и того же пространства имеют одинаковые мощность, называемый гильбертовым измерением пространства.[60] Например, поскольку л2(B) имеет ортонормированный базис, индексируемый B, его гильбертова размерность равна мощности B (которое может быть конечным целым, счетным или несчетным количественное числительное ).
Как следствие личности Парсеваля, если {еk}k ∈ B является ортонормированным базисом ЧАС, то карта Φ : ЧАС → л2(B) определяется Φ(Икс) = ⟨X, еk⟩k∈B является изометрическим изоморфизмом гильбертовых пространств: это биективное линейное отображение такое, что
для всех Икс, у ∈ ЧАС. В количественное числительное из B гильбертова размерность ЧАС. Таким образом, каждое гильбертово пространство изометрически изоморфно пространству последовательностей л2(B) для некоторого набора B.
Разделимые пространства
По определению гильбертово пространство отделяемый при условии, что он содержит плотное счетное подмножество. Наряду с леммой Цорна это означает, что гильбертово пространство сепарабельно тогда и только тогда, когда оно допускает счетный ортонормированный базис. Поэтому все бесконечномерные сепарабельные гильбертовы пространства изометрически изоморфны л2.
В прошлом, как часть определения, гильбертовы пространства часто требовалось разделить.[61] Большинство пространств, используемых в физике, разделимы, и, поскольку все они изоморфны друг другу, любое бесконечномерное сепарабельное гильбертово пространство часто называют "то Гильбертово пространство »или просто« Гильбертово пространство ».[62] Даже в квантовая теория поля, большинство гильбертовых пространств на самом деле сепарабельны, как это предусмотрено Аксиомы Вайтмана. Однако иногда утверждают, что неразделимые гильбертовы пространства также важны в квантовой теории поля, примерно потому, что системы в теории обладают бесконечным числом степени свободы и любой бесконечный Тензорное произведение Гильберта (пространств размерности больше единицы) неразделимо.[63] Например, бозонное поле естественно рассматривать как элемент тензорного произведения, факторы которого представляют гармонические осцилляторы в каждой точке пространства. С этой точки зрения пространство естественных состояний бозона может показаться неразделимым пространством.[63] Однако только небольшое разделяемое подпространство полного тензорного произведения может содержать физически значимые поля (на которых можно определить наблюдаемые). Другое неразделимое гильбертово пространство моделирует состояние бесконечного набора частиц в неограниченной области пространства. Ортонормированный базис пространства индексируется плотностью частиц, непрерывным параметром, и, поскольку набор возможных плотностей неисчислим, базис не исчисляем.[63]
Ортогональные дополнения и проекции
Если S является подмножеством гильбертова пространства ЧАС, множество векторов, ортогональных S определяется
S⊥ это закрыто подпространство ЧАС (можно легко доказать, используя линейность и непрерывность скалярного произведения) и, таким образом, образует гильбертово пространство. Если V является замкнутым подпространством в ЧАС, тогда V⊥ называется ортогональное дополнение из V. Фактически, каждый Икс ∈ ЧАС тогда можно записать однозначно как Икс = v + ш, с v ∈ V и ш ∈ V⊥. Следовательно, ЧАС - внутренняя прямая сумма Гильберта V и V⊥.
Линейный оператор пV : ЧАС → ЧАС что отображает Икс к v называется ортогональная проекция на V. Существует естественный взаимно однозначное соответствие между множеством всех замкнутых подпространств ЧАС и множество всех ограниченных самосопряженных операторов п такой, что п2 = п. Конкретно,
- Теорема. Ортогональная проекция пV является самосопряженным линейным оператором на ЧАС нормы ≤ 1 со свойством п2
V = пV. Более того, любой самосопряженный линейный оператор E такой, что E2 = E имеет форму пV, куда V это диапазон E. Для каждого Икс в ЧАС, пV(Икс) уникальный элемент v из V что минимизирует расстояние ||Икс − v||.
Это обеспечивает геометрическую интерпретацию пV(Икс): это наилучшее приближение к Икс элементами V.[64]
Прогнозы пU и пV называются взаимно ортогональными, если пUпV = 0. Это эквивалентно U и V ортогональны как подпространства ЧАС. Сумма двух прогнозов пU и пV это проекция, только если U и V ортогональны друг другу, и в этом случае пU + пV = пU+V. Составной пUпV вообще не проекция; на самом деле композиция является проекцией тогда и только тогда, когда две проекции коммутируют, и в этом случае пUпV = пU∩V.
Ограничивая область области гильбертовым пространством V, ортогональная проекция пV рождает проекционное отображение π : ЧАС → V; это примыкающий к отображение включения
означающий, что
для всех Икс ∈ V и у ∈ ЧАС.
Операторная норма ортогональной проекции пV на ненулевое замкнутое подпространство V равно 1:
Каждое замкнутое подпространство V гильбертова пространства, следовательно, является образом оператора п нормы один такой, что п2 = п. Свойство обладания подходящими операторами проекции характеризует гильбертовы пространства:[65]
- Банахово пространство размерности выше 2 является (изометрически) гильбертовым пространством тогда и только тогда, когда для любого замкнутого подпространства V, есть оператор пV нормы один, чей образ V такой, что п2
V = пV.
Хотя этот результат характеризует метрическую структуру гильбертова пространства, структура гильбертова пространства как топологическое векторное пространство сам по себе может быть охарактеризован с точки зрения наличия дополнительных подпространств:[66]
- Банахово пространство Икс топологически и линейно изоморфно гильбертову пространству тогда и только тогда, когда каждому замкнутому подпространству V, существует замкнутое подпространство W такой, что Икс равна внутренней прямой сумме V ⊕ W.
Ортогональное дополнение удовлетворяет еще нескольким элементарным результатам. Это монотонная функция в том смысле, что если U ⊂ V, тогда V⊥ ⊆ U⊥ с равенством выполняется тогда и только тогда, когда V содержится в закрытие из U. Этот результат является частным случаем Теорема Хана – Банаха. Замыкание подпространства можно полностью охарактеризовать в терминах ортогонального дополнения: если V является подпространством ЧАС, то закрытие V равно V⊥⊥. Таким образом, ортогональное дополнение есть Связь Галуа на частичный заказ подпространств гильбертова пространства. В общем, ортогональное дополнение к сумме подпространств - это пересечение ортогональных дополнений:[67]
Если Vя дополнительно закрыты, то
Спектральная теория
Есть хорошо развитая спектральная теория для самосопряженных операторов в гильбертовом пространстве, что примерно аналогично изучению симметричные матрицы над вещественными или самосопряженными матрицами над комплексными числами.[68] В том же смысле можно получить «диагонализацию» самосопряженного оператора как подходящую сумму (фактически интеграл) ортогональных проекционных операторов.
В спектр оператора Т, обозначенный σ(Т), - набор комплексных чисел λ такой, что Т − λ отсутствует непрерывный инверс. Если Т ограничен, то спектр всегда компактный набор в комплексной плоскости и лежит внутри диска |z| ≤ ||Т||. Если Т самосопряженный, то спектр действительный. Фактически он содержится в интервале [м, M] куда
Более того, м и M оба фактически содержатся в спектре.
Собственные подпространства оператора Т даны
В отличие от конечных матриц, не каждый элемент спектра Т должно быть собственным значением: линейный оператор Т − λ может отсутствовать только обратное, потому что оно не сюръективно. Элементы спектра оператора в общем смысле известны как спектральные значения. Поскольку спектральные значения не обязательно должны быть собственными значениями, спектральное разложение часто бывает более тонким, чем в конечных измерениях.
Тем не менее спектральная теорема самосопряженного оператора Т принимает особенно простой вид, если, кроме того, Т считается компактный оператор. В спектральная теорема для компактных самосопряженных операторов состояния:[69]
- Компактный самосопряженный оператор Т имеет только счетное (или конечное) число спектральных значений. Спектр Т не имеет предельная точка в комплексной плоскости, кроме, возможно, нуля. Собственные подпространства Т разлагать ЧАС в ортогональную прямую сумму:
- Более того, если Eλ обозначает ортогональную проекцию на собственное подпространство ЧАСλ, тогда
- где сумма сходится по норме на B (ЧАС).
Эта теорема играет фундаментальную роль в теории интегральные уравнения, поскольку многие интегральные операторы компактны, в частности те, которые возникают из Операторы Гильберта – Шмидта.
Общая спектральная теорема для самосопряженных операторов включает в себя своего рода операторнозначные Интеграл Римана – Стилтьеса., а не бесконечное суммирование.[70] В призрачная семья связано с Т сопоставляет каждому действительному числу λ оператор Eλ, которая является проекцией на нулевое пространство оператора (Т − λ)+, где положительная часть самосопряженного оператора определяется равенством
Операторы Eλ монотонно возрастают относительно частичного порядка, определенного на самосопряженных операторах; собственные значения в точности соответствуют скачкам. Есть спектральная теорема, утверждающая
Под интегралом понимается интеграл Римана – Стилтьеса, сходящийся по норме на B (ЧАС). В частности, имеется обычное скалярнозначное интегральное представление
В чем-то похожее спектральное разложение справедливо для нормальных операторов, хотя, поскольку спектр теперь может содержать невещественные комплексные числа, операторнозначная мера Стилтьеса dEλ вместо этого должен быть заменен разрешение личности.
Основное применение спектральных методов - это теорема о спектральном отображении, что позволяет применить к самосопряженному оператору Т любая непрерывная комплексная функция ж определены на спектре Т образуя интеграл
Результирующий непрерывное функциональное исчисление имеет приложения, в частности, псевдодифференциальные операторы.[71]
Спектральная теория неограниченный самосопряженные операторы лишь незначительно сложнее, чем для ограниченных операторов. Спектр неограниченного оператора определяется точно так же, как и для ограниченных операторов: λ является спектральным значением, если оператор резольвенты
не может быть четко определенным непрерывным оператором. Самосопряженность Т по-прежнему гарантирует, что спектр настоящий. Таким образом, основная идея работы с неограниченными операторами состоит в том, чтобы вместо этого смотреть на резольвенту рλ куда λ нереально. Это ограниченный нормальный оператор, допускающий спектральное представление, которое затем может быть перенесено в спектральное представление Т сам. Подобная стратегия используется, например, для изучения спектра оператора Лапласа: вместо того, чтобы обращаться к оператору напрямую, вместо этого он выглядит как связанная резольвента, такая как Потенциал Рисса или же Бесселев потенциал.
Точная версия спектральной теоремы в этом случае:[72]
- Для плотно определенного самосопряженного оператора Т в гильбертовом пространстве ЧАС, соответствует уникальный разрешение личности E на борелевских множествах ℝ, так что
- для всех Икс ∈ D(Т) и у ∈ ЧАС. Спектральная мера E сосредоточен на спектре Т.
Существует также версия спектральной теоремы, которая применяется к неограниченным нормальным операторам.
В популярной культуре
Томас Пинчон представил вымышленного персонажа Сэмми Гильберта-Спесса (каламбур на «Гильбертовом пространстве») в своем романе 1973 года, Радуга гравитации. Гильберта-Спесса сначала описывают как «вездесущего двойного агента», а затем как «по крайней мере двойного агента».[73] В романе ранее упоминалась работа немецкого математика. Курт Гёдель с Теоремы о неполноте,[74] который показал, что Программа Гильберта Формализованный план Гильберта объединить математику в единый набор аксиом оказался невозможным.[75]
Смотрите также
- Банахово пространство - Полное нормированное векторное пространство
- Основная теорема гильбертовых пространств
- Пространство Адамара
- Гильбертова алгебра
- C * -модуль Гильберта
- Гильбертово многообразие
- L-полувнутренний продукт - Обобщение внутренних продуктов, применимое ко всем нормированным пространствам
- Локально выпуклое топологическое векторное пространство - Векторное пространство с топологией, определяемой выпуклыми открытыми множествами
- Теория операторов
- Операторские топологии
- Оснащенное гильбертово пространство - Конструкция, связывающая изучение "связанных" и непрерывных собственных значений в функциональном анализе.
- Топологическое векторное пространство - Векторное пространство с понятием близости
Замечания
Примечания
- ^ Марсден 1974, §2.8
- ^ Математический материал в этом разделе можно найти в любом хорошем учебнике по функциональному анализу, например в Дьедонне (1960), Хьюитт и Стромберг (1965), Рид и Саймон (1980) или же Рудин (1987).
- ^ Шефер и Вольф, 1999 г. С. 122-202.
- ^ Дьедонне 1960, §6.2
- ^ Дьедонне 1960
- ^ Во многом благодаря работе Герман Грассманн, по настоянию Август Фердинанд Мёбиус (Бойер и Мерцбах 1991, стр. 584–586). Первое современное аксиоматическое описание абстрактных векторных пространств в конечном итоге появилось в Джузеппе Пеано счет 1888 г. (Граттан-Гиннесс 2000, §5.2.2; О'Коннор и Робертсон 1996 ).
- ^ Подробный отчет об истории гильбертовых пространств можно найти в Бурбаки 1987.
- ^ Шмидт 1908
- ^ Титчмарш 1946, §IX.1
- ^ Лебег 1904. Более подробную информацию об истории теории интеграции можно найти в Бурбаки (1987) и Сакс (2005).
- ^ Бурбаки 1987.
- ^ Данфорд и Шварц 1958, §IV.16
- ^ В Данфорд и Шварц (1958, §IV.16), что каждый линейный функционал на L2[0,1] представлен интеграцией совместно отнесен к Фреше (1907) и Рис (1907). Общий результат о том, что двойственное к гильбертову пространству отождествляется с самим гильбертовым пространством, можно найти в Рис (1934).
- ^ фон Нейман 1929.
- ^ Клайн 1972, п. 1092
- ^ Гильберт, Нордхайм и фон Нейман, 1927 г.
- ^ а б Вейль 1931.
- ^ Пруговечки 1981, стр. 1–10.
- ^ а б фон Нейман 1932
- ^ Халмос 1957, Раздел 42.
- ^ Хьюитт и Стромберг, 1965 г..
- ^ а б Берс, Джон и Шехтер 1981.
- ^ Джусти 2003.
- ^ Штейн 1970
- ^ Подробности можно найти в Уорнер (1983).
- ^ Общий справочник по пространствам Харди - это книга Дюрен (1970).
- ^ Кранц 2002, §1.4
- ^ Кранц 2002, §1.5
- ^ Молодой 1988, Глава 9.
- ^ Более подробную информацию о методах конечных элементов с этой точки зрения можно найти в Бреннер и Скотт (2005).
- ^ Рид и Саймон 1980
- ^ Рассмотрение рядов Фурье с этой точки зрения доступно, например, в Рудин (1987) или же Фолланд (2009).
- ^ Халмос 1957, §5
- ^ Бахман, Наричи и Бекенштейн 2000
- ^ Штайн и Вайс, 1971 г., §IV.2.
- ^ Ланцош 1988, стр. 212–213
- ^ Ланцош 1988, Уравнение 4-3.10
- ^ Классическим справочником по спектральным методам является Курант и Гильберт 1953. Более актуальная учетная запись Рид и Саймон 1975.
- ^ Кац 1966
- ^ фон Нейман 1955
- ^ Молодой 1988, п. 23.
- ^ Кларксон 1936.
- ^ Рудин 1987, Теорема 4.10
- ^ Данфорд и Шварц 1958, II.4.29
- ^ Рудин 1987, Теорема 4.11
- ^ Бланше, Жерар; Шарбит, Морис (2014). Цифровая обработка сигналов и изображений с использованием MATLAB. Цифровая обработка сигналов и изображений. 1 (Второе изд.). Нью-Джерси: Уайли. С. 349–360. ISBN 978-1848216402.
- ^ Weidmann 1980, Теорема 4.8
- ^ Weidmann 1980, §4.5
- ^ Бутаццо, Джаквинта и Хильдебрандт 1998, Теорема 5.17
- ^ Халмос 1982, Задача 52, 58
- ^ Рудин 1973
- ^ Трев 1967, Глава 18
- ^ Видеть Пруговечки (1981), Рид и Саймон (1980), Глава VIII) и Фолланд (1989).
- ^ Пруговечки 1981, III, §1.4
- ^ Данфорд и Шварц 1958, IV.4.17-18
- ^ Weidmann 1980, §3.4
- ^ Кадисон и Рингроуз, 1983, Теорема 2.6.4
- ^ Данфорд и Шварц 1958, §IV.4.
- ^ Для случая конечных наборов индексов см., Например, Халмос 1957, §5. Для бесконечных наборов индексов см. Weidmann 1980, Теорема 3.6.
- ^ Левитан 2001. Многие авторы, такие как Данфорд и Шварц (1958, §IV.4), назовем это просто размерностью. Если гильбертово пространство не является конечномерным, это не то же самое, что его размерность как линейного пространства (мощность базиса Гамеля).
- ^ Пруговечки 1981, I, §4.2
- ^ фон Нейман (1955) определяет гильбертово пространство через счетный гильбертовый базис, который составляет изометрический изоморфизм с л2. Соглашение по-прежнему сохраняется в самых строгих трактовках квантовой механики; см. например Собрино 1996 г., Приложение Б.
- ^ а б c Streater & Wightman 1964, стр. 86–87
- ^ Молодой 1988, Теорема 15.3
- ^ Какутани 1939
- ^ Линденштраус и Цафрири, 1971 г.
- ^ Халмос 1957, §12
- ^ Общий обзор спектральной теории в гильбертовых пространствах можно найти в Рис и С.-Надь (1990). Более сложное изложение на языке C * -алгебр содержится в Рудин (1973) или же Кадисон и Рингроуз (1997)
- ^ См., Например, Рис и С.-Надь (1990, Глава VI) или Weidmann 1980, Глава 7. Этот результат был уже известен Шмидт (1908) в случае операторов, возникающих из целочисленных ядер.
- ^ Рис и С.-Надь 1990, §§107–108
- ^ Шубин 1987 г.
- ^ Рудин 1973, Теорема 13.30.
- ^ "H - Гильберт-Спесс, Сэмми". Томас Пинчон вики: Радуга гравитации. Получено 2018-10-23.
- ^ «Теорема G - Гёделя». Томас Пинчон вики: Радуга гравитации. Получено 2018-10-23.
- ^ Томас, Пинчон (1973). Радуга гравитации. Викинг Пресс. С. 217, 275. ISBN 978-0143039945.
Рекомендации
- Бахман, Джордж; Наричи, Лоуренс; Бекенштейн, Эдвард (2000), Фурье и вейвлет-анализ, Universitext, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-98899-3, МИСТЕР 1729490.
- Берс, Липман; Джон, Фриц; Шехтер, Мартин (1981), Уравнения с частными производными, Американское математическое общество, ISBN 978-0-8218-0049-2.
- Бурбак, Николази (1986), Спектральные теории, Элементы математики, Берлин: Springer-Verlag, ISBN 978-0-201-00767-1.
- Бурбаки, Николас (1987), Топологические векторные пространства, Элементы математики, Берлин: Springer-Verlag, ISBN 978-3-540-13627-9.
- Бойер, Карл Бенджамин; Мерцбах, Ута Ц (1991), История математики (2-е изд.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
- Brenner, S .; Скотт, Р. Л. (2005), Математическая теория методов конечных элементов (2-е изд.), Springer, ISBN 978-0-387-95451-6.
- Бутаццо, Джузеппе; Джакинта, Мариано; Хильдебрандт, Стефан (1998), Одномерные вариационные задачи, Оксфордская серия лекций по математике и ее приложениям, 15, The Clarendon Press Oxford University Press, ISBN 978-0-19-850465-8, МИСТЕР 1694383.
- Кларксон, Дж. А. (1936), "Равномерно выпуклые пространства", Пер. Амер. Математика. Soc., 40 (3): 396–414, Дои:10.2307/1989630, JSTOR 1989630.
- Курант, Ричард; Гильберт, Дэвид (1953), Методы математической физики. я, Interscience.
- Дьедонне, Жан (1960), Основы современного анализа, Academic Press.
- Дирак, П.А. (1930), Принципы квантовой механики, Оксфорд: Clarendon Press.
- Dunford, N .; Шварц, Дж. (1958), Линейные операторы, части I и II, Wiley-Interscience.
- Дюрен, П. (1970), Теория Hп-Пространства, Нью-Йорк: Academic Press.
- Фолланд, Джеральд Б. (2009), Фурье-анализ и его применение (Перепечатка Wadsworth and Brooks / Cole 1992 ed.), Книжный магазин Американского математического общества, ISBN 978-0-8218-4790-9.
- Фолланд, Джеральд Б. (1989), Гармонический анализ в фазовом пространстве, Анналы математических исследований, 122, Издательство Принстонского университета, ISBN 978-0-691-08527-2.
- Фреше, Морис (1907), "Sur les ensembles de fonctions et les opérations linéaires", C. R. Acad. Sci. Париж, 144: 1414–1416.
- Фреше, Морис (1904), "Sur les opérations linéaires", Труды Американского математического общества, 5 (4): 493–499, Дои:10.2307/1986278, JSTOR 1986278.
- Джусти, Энрико (2003), Прямые методы вариационного исчисления, World Scientific, ISBN 978-981-238-043-2.
- Граттан-Гиннесс, Айвор (2000), Поиски математических корней, 1870–1940 гг., Принстонские книги в мягкой обложке, Princeton University Press, ISBN 978-0-691-05858-0, МИСТЕР 1807717.
- Халмос, Пол (1957), Введение в гильбертово пространство и теорию спектральной кратности, Chelsea Pub. Co
- Халмос, Пол (1982), Книга проблем гильбертова пространства, Springer-Verlag, ISBN 978-0-387-90685-0.
- Хьюитт, Эдвин; Стромберг, Карл (1965), Реальный и абстрактный анализ, Нью-Йорк: Springer-Verlag.
- Гильберт, Дэвид; Нордхейм, Лотар (Вольфганг); фон Нейман, Джон (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen, 98: 1–30, Дои:10.1007 / BF01451579, S2CID 120986758[мертвая ссылка ].
- Кац, Марк (1966), «Можно ли услышать форму барабана?», Американский математический ежемесячный журнал, 73 (4, часть 2): 1–23, Дои:10.2307/2313748, JSTOR 2313748.
- Кадисон, Ричард V .; Рингроуз, Джон Р. (1997), Основы теории операторных алгебр. Vol. я, Аспирантура по математике, 15, Провиденс, Р.И.: Американское математическое общество, ISBN 978-0-8218-0819-1, МИСТЕР 1468229.
- Кадисон, Ричард V .; Рингроуз, Джон Р. (1983), Основы теории операторных алгебр. I: Элементарная теория, Нью-Йорк: Academic Press, Inc.
- Какутани, Шизуо (1939), «Некоторые характеристики евклидова пространства», Японский математический журнал, 16: 93–97, Дои:10.4099 / jjm1924.16.0_93, МИСТЕР 0000895.
- Клайн, Моррис (1972), Математическая мысль от древних времен до наших дней, Том 3 (3-е изд.), Oxford University Press (опубликовано в 1990 г.), ISBN 978-0-19-506137-6.
- Колмогоров Андрей; Фомин, Сергей В. (1970), Вводный реальный анализ (Пересмотренное английское издание, перевод Ричарда А. Сильвермана (1975) изд.), Dover Press, ISBN 978-0-486-61226-3.
- Кранц, Стивен Г. (2002), Теория функций нескольких комплексных переменных, Провиденс, Р.И.: Американское математическое общество, ISBN 978-0-8218-2724-6.
- Ланцош, Корнелиус (1988), Прикладной анализ (Перепечатка изд. Прентис-Холла 1956 г.), Dover Publications, ISBN 978-0-486-65656-4.
- Лебег, Анри (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Готье-Виллар.
- Левитан, Б. (2001) [1994], «Гильбертово пространство», Энциклопедия математики, EMS Press.
- Lindenstrauss, J .; Цафрири, Л. (1971), "О проблеме дополненных подпространств", Израильский математический журнал, 9 (2): 263–269, Дои:10.1007 / BF02771592, ISSN 0021-2172, МИСТЕР 0276734, S2CID 119575718.
- Марсден, Джеррольд Э. (1974), Элементарный классический анализ, W.H. Freeman and Co., МИСТЕР 0357693.
- фон Нейман, Джон (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen, 102: 49–131, Дои:10.1007 / BF01782338, S2CID 121249803.
- Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства. Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- фон Нейман, Джон (1932), "Физические приложения эргодической гипотезы", Proc Natl Acad Sci USA, 18 (3): 263–266, Bibcode:1932ПНАС ... 18..263Н, Дои:10.1073 / pnas.18.3.263, JSTOR 86260, ЧВК 1076204, PMID 16587674.
- фон Нейман, Джон (1955), Математические основы квантовой механики, Принстонские вехи в математике, перевод Бейера, Роберта Т., Princeton University Press (опубликовано в 1996 г.), ISBN 978-0-691-02893-4, МИСТЕР 1435976.
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (1996), «Абстрактные линейные пространства», Архив истории математики MacTutor, Сент-Эндрюсский университет.
- Пруговечки, Эдуард (1981), Квантовая механика в гильбертовом пространстве (2-е изд.), Dover (опубликовано в 2006 г.), ISBN 978-0-486-45327-9.
- Рид, Майкл; Саймон, Барри (1980), Функциональный анализ, Методы современной математической физики, Academic Press, ISBN 978-0-12-585050-6.
- Рид, Майкл; Саймон, Барри (1975), Фурье-анализ, самосопряженность, Методы современной математической физики, Academic Press, ISBN 9780125850025.
- Рис, Фриджес (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", C. R. Acad. Sci. Париж, 144: 1409–1411.
- Рис, Фриджес (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Математика. Сегед, 7: 34–38.
- Рис, Фриджес; Sz.-Nagy, Béla (1990), Функциональный анализ, Дувр, ISBN 978-0-486-66289-3.
- Рудин, Вальтер (1973). Функциональный анализ. Международная серия по чистой и прикладной математике. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: Макгроу-Хилл Наука / Инженерия / Математика. ISBN 9780070542259.
- Рудин, Вальтер (1987), Реальный и комплексный анализ, МакГроу-Хилл, ISBN 978-0-07-100276-9.
- Сакс, Станислав (2005), Теория интеграла (2-е изд. Дувра), Дувр, ISBN 978-0-486-44648-6; первоначально опубликовано Monografje Matematyczne, т. 7, Варшава, 1937.
- Шефер, Гельмут Х.; Вольф, Манфред П. (1999). Топологические векторные пространства. GTM. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Шмидт, Эрхард (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Ренд. Circ. Мат. Палермо, 25: 63–77, Дои:10.1007 / BF03029116, S2CID 120666844.
- Шубин, М.А. (1987), Псевдодифференциальные операторы и спектральная теория, Серия Спрингера по советской математике, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-13621-7, МИСТЕР 0883081.
- Собрино, Луис (1996), Элементы нерелятивистской квантовой механики, Ривер Эдж, Нью-Джерси: World Scientific Publishing Co. Inc., Bibcode:1996lnrq.book ..... S, Дои:10.1142/2865, ISBN 978-981-02-2386-1, МИСТЕР 1626401.
- Стюарт, Джеймс (2006), Исчисление: концепции и контексты (3-е изд.), Томсон / Брукс / Коул.
- Штейн, E (1970), Сингулярные интегралы и дифференцируемость функций., Princeton Univ. Нажмите, ISBN 978-0-691-08079-6.
- Штейн, Элиас; Вайс, Гвидо (1971), Введение в анализ Фурье на евклидовых пространствах, Принстон, Нью-Джерси: Издательство Принстонского университета, ISBN 978-0-691-08078-9.
- Стритер, Рэй; Вайтман, Артур (1964), PCT, спин, статистика и все такое, W. A. Benjamin, Inc.
- Тешл, Джеральд (2009). Математические методы в квантовой механике; С приложениями к операторам Шредингера. Провиденс: Американское математическое общество. ISBN 978-0-8218-4660-5..
- Титчмарш, Эдвард Чарльз (1946), Разложения по собственным функциям, часть 1, Оксфордский университет: Clarendon Press.
- Трев, Франсуа (1967), Топологические векторные пространства, распределения и ядра, Academic Press.
- Уорнер, Фрэнк (1983), Основы дифференцируемых многообразий и групп Ли, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-90894-6.
- Вайдманн, Иоахим (1980), Линейные операторы в гильбертовых пространствах, Тексты для выпускников по математике, 68, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-90427-6, МИСТЕР 0566954.
- Вейль, Германн (1931), Теория групп и квантовая механика (Англ. Изд. 1950 г.), Dover Press, ISBN 978-0-486-60269-1.
- Молодой, Николай (1988), Введение в гильбертово пространство, Издательство Кембриджского университета, ISBN 978-0-521-33071-8, Zbl 0645.46024.
внешняя ссылка
 СМИ, связанные с Гильбертово пространство в Wikimedia Commons
СМИ, связанные с Гильбертово пространство в Wikimedia Commons- «Гильбертово пространство», Энциклопедия математики, EMS Press, 2001 [1994]
- Гильбертово пространство в Mathworld
- 245B, примечания 5: Гильбертовы пространства к Теренс Тао


















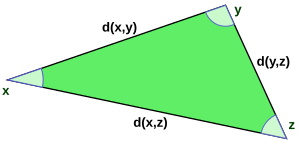


























![{displaystyle - {frac {mathrm {d}} {mathrm {d} x}} left [p (x) {frac {mathrm {d} y} {mathrm {d} x}} ight] + q (x) y = лямбда w (x) y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4e93c4082311667644e8554f78774b963ffb0e)

















































































