Комплексное число - Complex number

Комплексное число можно визуально представить в виде пары чисел (а, б) формирование вектора на диаграмме, называемой Диаграмма Аргана, представляющий комплексная плоскость. «Re» - действительная ось, «Im» - мнимая ось, а я удовлетворяет я² = −1.

А комплексное число это номер что может быть выражено в форме а + би, куда а и б находятся действительные числа, и я представляет мнимая единица, удовлетворяющая уравнению я² = −1. Поскольку никакое действительное число не удовлетворяет этому уравнению, я называется мнимое число. Для комплексного числа а + би, а называется реальная часть, и б называется мнимая часть. Набор комплексных чисел обозначается символом ${displaystyle mathbb {C} }$. Несмотря на историческую номенклатуру «воображаемое», комплексные числа рассматриваются в математических науках столь же «реальными», как и действительные числа, и являются фундаментальными во многих аспектах научного описания мира природы.^{[примечание 1][1][2][3][4]}

Комплексные числа позволяют решать некоторые уравнения, не имеющие решений в действительных числах. Например, уравнение

${displaystyle (x+1)^{2}=-9}$

не имеет реального решения, так как квадрат действительного числа не может быть отрицательным. Однако комплексные числа позволяют решить эту проблему. Идея состоит в том, чтобы продлевать реальные числа с неопределенный я (иногда называемая мнимой единицей), удовлетворяющая соотношению я² = −1, так что решения уравнений, подобных предыдущему, могут быть найдены. В этом случае решениями являются −1 + 3я и −1 − 3я, в чем можно убедиться, используя тот факт, что я² = −1:

${displaystyle ((-1+3i)+1)^{2}=(3i)^{2}=left(3^{2}ight)left(i^{2}ight)=9(-1)=-9,}$

${displaystyle ((-1-3i)+1)^{2}=(-3i)^{2}=(-3)^{2}left(i^{2}ight)=9(-1)=-9.}$

Согласно основная теорема алгебры, все полиномиальные уравнения с действительными или комплексными коэффициентами в одной переменной имеют решение в комплексных числах. Напротив, некоторые полиномиальные уравнения с действительными коэффициентами не имеют решения в действительных числах. Итальянский математик XVI века Джероламо Кардано приписывают введение комплексных чисел - в его попытках найти решения кубические уравнения.^[5]

Формально комплексную систему счисления можно определить как алгебраическое расширение обычных действительных чисел на мнимое число я.^[6] Это означает, что комплексные числа можно складывать, вычитать и умножать как многочлены в переменной. я, по правилу, что я² = −1. Кроме того, комплексные числа также можно разделить на ненулевые комплексные числа.^[3] В целом комплексная система счисления - это поле.

Геометрически комплексные числа расширяют понятие одномерный числовая строка к двумерный комплексная плоскость, используя Горизонтальная ось для реальной части, и вертикальная ось для мнимой части. Комплексное число а + би можно отождествить с точкой (а, б) в комплексной плоскости. Комплексное число, действительная часть которого равна нулю, называется чисто воображаемый, а точки этих чисел лежат на вертикальной оси комплексной плоскости. Точно так же комплексное число, мнимая часть которого равна нулю, можно рассматривать как действительное число, точка которого лежит на горизонтальной оси комплексной плоскости. Комплексные числа также могут быть представлены в полярной форме, которая связывает каждое комплексное число с его расстоянием от начала координат (его величиной) и определенным углом, известным как аргумент комплексного числа.

Геометрическая идентификация комплексных чисел с комплексной плоскостью, которая является Евклидова плоскость (${displaystyle mathbb {R} ^{2}}$), превращает их структуру в настоящую двумерную векторное пространство очевидно. Действительная и мнимая части комплексного числа могут быть взяты как компоненты вектора - относительно канонического стандартная основа. Таким образом, сложение комплексных чисел сразу же изображается как обычное покомпонентное сложение векторов. Однако комплексные числа позволяют использовать более богатую алгебраическую структуру, включающую дополнительные операции, которые не обязательно доступны в векторном пространстве. Например, умножение двух комплексных чисел всегда снова дает комплексное число, и его не следует принимать за обычные «произведения», включающие векторы, такие как скалярное умножение, то скалярное произведение или другие (полуторные) линейные формы, доступен во многих векторных пространствах; и широко эксплуатируемые векторный продукт существует только в ориентация -зависимая форма в трех измерениях.

Определение

Иллюстрация комплексная плоскость. Действительная часть комплексного числа z = Икс + иу является Икс, а его мнимая часть равна у.

Комплексное число - это число в форме а + би, куда а и б находятся действительные числа, и я неопределенное удовлетворение я² = −1. Например, 2 + 3я - комплексное число.^[7][3]

Таким образом, комплексное число определяется как многочлен с действительными коэффициентами в единственном неопределенном я, для которого соотношение я² + 1 = 0 навязывается. На основе этого определения комплексные числа можно складывать и умножать, используя сложение и умножение многочленов. Соотношение я² + 1 = 0 индуцирует равенства я^4k = 1, я^4k+1 = я, я^4k+2 = −1, и я^4k+3 = −я, которые верны для всех целых чисел k; они позволяют уменьшить любой многочлен, полученный в результате сложения и умножения комплексных чисел, до линейного многочлена от я, снова формы а + би с действительными коэффициентами а, б.

Настоящее число а называется реальная часть комплексного числа а + би; реальное число б называется его мнимая часть. Подчеркнем, что мнимая часть не включает фактор я; то есть мнимая часть б, нет би.^[8][9][3]

Формально комплексные числа определяются как кольцо частного из кольцо многочленов в неопределенном я, посредством идеальный порожденный полиномом я² + 1 (видеть ниже ).^[6]

Обозначение

Настоящее число а можно рассматривать как комплексное число а + 0я, мнимая часть которого равна 0. Чисто мнимое число би это комплексное число 0 + би, действительная часть которого равна нулю. Как и в случае с полиномами, обычно пишут а за а + 0я и би за 0 + би. Более того, когда мнимая часть отрицательна, то есть б = −| б | < 0, это принято писать а − | б | я вместо а + (−| б |)я; например, для б = −4, 3 − 4я можно написать вместо 3 + (−4)я.

Поскольку умножение неопределенных я а вещественное число коммутативно от многочленов с действительными коэффициентами, многочлен а + би можно записать как а + ib. Часто это целесообразно для мнимых частей, обозначенных выражениями, например, когда б радикальный.^[10]

Действительная часть комплексного числа z обозначается Re (z) или же ℜ (z); мнимая часть комплексного числа z обозначается Я(z) или же ℑ (z).^[1] Например,

${displaystyle operatorname {Re} (2+3i)=2quad }$ и ${displaystyle quad operatorname {Im} (2+3i)=3.}$

В набор всех комплексных чисел обозначается ${displaystyle mathbf {C} }$ (прямой жирный шрифт) или ${displaystyle mathbb {C} }$ (классная доска жирным шрифтом ).^[1]

В некоторых дисциплинах, особенно в электромагнетизм и электротехника, j используется вместо я в качестве я часто используется для обозначения электрический ток.^[11] В этих случаях комплексные числа записываются как а + Ъ, или же а + jb.

Визуализация

Основная статья: Комплексная плоскость

Комплексное число z, как точка (красная) и ее вектор положения (синий)

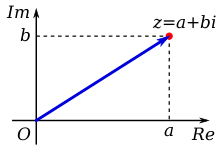
Комплексное число z таким образом можно отождествить с упорядоченная пара (Re (z), Я(z)) действительных чисел, которые, в свою очередь, можно интерпретировать как координаты точки в двумерном пространстве. Ближайшее пространство - это евклидова плоскость с подходящими координатами, которая затем называется комплексная плоскость или же Диаграмма Аргана,^[12][13][14] названный в честь Жан-Робер Арган. Еще одно заметное пространство, на которое можно проецировать координаты, - это двумерная поверхность сферы, которую затем называют Сфера Римана.

Декартова комплексная плоскость

Определение комплексных чисел, включающих два произвольных действительных значения, сразу предполагает использование декартовых координат в комплексной плоскости. Горизонтальный (настоящий) ось обычно используется для отображения реальной части с увеличивающимися значениями вправо, а мнимая часть отмечает вертикальную (воображаемый) ось с увеличением значений вверх.

Нанесенный на карту номер может рассматриваться либо как согласованная точка, либо как вектор положения от начала до этой точки. Значения координат комплексного числа z можно таким образом выразить Декартово, прямоугольный, или же алгебраический форма.

Примечательно, что операции сложения и умножения принимают очень естественный геометрический характер, когда комплексные числа рассматриваются как векторы положения: сложение соответствует векторное сложение, а умножение (см. ниже ) соответствует умножению их величин и сложению углов, которые они образуют с действительной осью. С этой точки зрения умножение комплексного числа на я соответствует вращению вектора положения против часовой стрелки на четверть повернуть (90° ) о происхождении - факт, который алгебраически может быть выражен следующим образом:

${displaystyle (a+bi)cdot i=ai+b(i)^{2}=-b+ai.}$

Полярная комплексная плоскость

Основная статья: Полярная система координат

«Полярная форма» перенаправляется сюда. Для многомерного аналога см. Полярное разложение.

Аргумент φ и модуль р найдите точку на комплексной плоскости.

Модуль и аргумент

Альтернативный вариант для координат на комплексной плоскости - это полярная система координат который использует расстояние до точки z от источник (О), а угол между положительная действительная ось и отрезок линии Унция против часовой стрелки. Это приводит к полярной форме комплексных чисел.

В абсолютная величина (или же модуль или же величина) комплексного числа z = Икс + йи является^[15]

${displaystyle r=|z|={sqrt {x^{2}+y^{2}}}.}$

Если z является действительным числом (то есть, если у = 0), тогда р = |Икс|. То есть абсолютное значение действительного числа равно его абсолютному значению как комплексного числа.

К Теорема Пифагора, абсолютное значение комплексного числа - это расстояние до начала координат точки, представляющей комплексное число в комплексная плоскость.

В аргумент из z (во многих приложениях называется «фазой» φ)^[14] это угол радиус Унция с положительной действительной осью и записывается как ${displaystyle arg(z)}$. Как и в случае модуля, аргумент можно найти из прямоугольной формы ${displaystyle x+yi}$^[16]—Применяя арктангенс к частному действительной части мнимой части. Используя тождество половинного угла, одной ветви арктанганса достаточно, чтобы покрыть диапазон аргумент-функция, (−π, π], и позволяет избежать более тонкого индивидуального анализа

${displaystyle varphi =arg(x+yi)={egin{cases}2arctan left({dfrac {y}{{sqrt {x^{2}+y^{2}}}+x}}ight)&{ ext{if }}x>0{ ext{ or }}yeq 0,pi &{ ext{if }}x<0{ ext{ and }}y=0,{ ext{undefined}}&{ ext{if }}x=0{ ext{ and }}y=0.end{cases}}}$

Обычно, как указано выше, основная стоимость в интервале (−π, π] выбран. Значения в диапазоне [0, 2π) получаются добавлением 2π- если значение отрицательное. Значение φ выражается в радианы в этой статье. Он может увеличиваться на любое целое число, кратное 2π и по-прежнему дают тот же угол, если смотреть на него лучи положительной действительной оси и от начала координат через z. Следовательно, функция arg иногда рассматривается как многозначный. Полярный угол для комплексного числа 0 не определен, но произвольный выбор полярного угла 0 является обычным явлением.

Значение φ равен результату atan2:

${displaystyle varphi =operatorname {atan2} left(operatorname {Im} (z),operatorname {Re} (z)ight).}$

Вместе, р и φ дать другой способ представления комплексных чисел, полярная форма, поскольку комбинация модуля и аргумента полностью определяет положение точки на плоскости. Восстановление исходных прямоугольных координат из полярной формы выполняется по формуле, называемой тригонометрическая форма

${displaystyle z=r(cos varphi +isin varphi ).}$

С помощью Формула Эйлера это можно записать как

${displaystyle z=re^{ivarphi }.}$

С использованием СНГ функция, иногда сокращенно

${displaystyle z=roperatorname {cis} varphi .}$

В обозначение угла, часто используется в электроника представлять фазор с амплитудой р и фаза φ, он записывается как^[17]

${displaystyle z=rangle varphi .}$

Сложные графы

Основные статьи: Раскраска домена и Риманова поверхность

График цветового круга выражения (z² − 1)(z − 2 − я)²/z² + 2 + 2я

При визуализации сложные функции, необходимы как комплексный ввод, так и вывод. Поскольку каждое комплексное число представлено в двух измерениях, визуальное отображение сложной функции потребует восприятия четырехмерное пространство, что возможно только в проекциях. Из-за этого были разработаны другие способы визуализации сложных функций.

В раскраска домена выходные размеры представлены цветом и яркостью соответственно. Каждая точка комплексной плоскости как область богато украшенный, обычно с цвет представляющий аргумент комплексного числа, и яркость представляющий величину. Темные пятна обозначают модули, близкие к нулю, более яркие пятна находятся дальше от начала координат, градация может быть прерывистой, но предполагается монотонной. Цвета часто меняются в зависимости от π/3 за 0 к 2π от красного, желтого, зеленого, голубого, синего до пурпурного. Эти сюжеты называются графики цветового круга. Это обеспечивает простой способ визуализации функций без потери информации. На картинке показаны нули для ±1, (2+я) и полюса на ±√−2−2я.

Римановы поверхности - еще один способ визуализировать сложные функции.^{[требуется дальнейшее объяснение ]} Римановы поверхности можно рассматривать как деформации комплексной плоскости; в то время как горизонтальные оси представляют реальный и мнимый входы, единственная вертикальная ось представляет только реальный или мнимый выход. Однако римановы поверхности построены таким образом, что их поворот на 180 градусов показывает воображаемый результат, и наоборот. В отличие от раскраски областей, римановы поверхности могут представлять многозначные функции подобно ${displaystyle {sqrt {z}}}$.

История

Решение в радикалы (без тригонометрические функции ) генерала кубическое уравнение содержит квадратные корни из отрицательные числа когда все три корня являются действительными числами, ситуация, которая не может быть исправлена ​​путем факторинга с помощью рациональный корень если кубика несводимый (так называемой казус несокрушимый ). Эта загадка привела итальянского математика Джероламо Кардано представить комплексные числа примерно в 1545 году,^[18] хотя его понимание было рудиментарным.

Работа над проблемой общих многочленов в конечном итоге привела к основная теорема алгебры, который показывает, что для комплексных чисел решение существует для каждого полиномиальное уравнение степени один или выше. Таким образом, комплексные числа образуют алгебраически замкнутое поле, где любое полиномиальное уравнение имеет корень.

Многие математики внесли свой вклад в разработку комплексных чисел. Правила сложения, вычитания, умножения и извлечения корня из комплексных чисел были разработаны итальянским математиком. Рафаэль Бомбелли.^[19] Более абстрактный формализм для комплексных чисел был развит ирландским математиком. Уильям Роуэн Гамильтон, который распространил эту абстракцию на теорию кватернионы.^[20]

Самая ранняя мимолетная ссылка на квадратные корни из отрицательные числа можно сказать, что это происходит в работе Греческий математик Герой Александрии в I веке ОБЪЯВЛЕНИЕ, где в его Stereometrica он считает, очевидно, ошибочно, объем невозможного усеченный из пирамида прийти к сроку ${displaystyle {sqrt {81-144}}=3i{sqrt {7}}}$ в его расчетах, хотя отрицательные величины не рассматривались в Эллинистическая математика а Герой просто заменил его положительным (${displaystyle {sqrt {144-81}}=3{sqrt {7}}}$).^[21]

Стимул к изучению комплексных чисел как самостоятельной темы впервые возник в 16 веке, когда алгебраические решения для корней кубический и квартика многочлены были открыты итальянскими математиками (см. Никколо Фонтана Тарталья, Джероламо Кардано ). Вскоре это было реализовано (но доказано намного позже)^[22] что эти формулы, даже если кто-то интересовался только действительными решениями, иногда требовали манипуляции с квадратными корнями из отрицательных чисел. Например, формула Тартальи для кубического уравнения вида ${displaystyle x^{3}=px+q}$^{[заметка 2]} дает решение уравнения Икс³ = Икс в качестве

${displaystyle { frac {1}{sqrt {3}}}left(left({sqrt {-1}}ight)^{1/3}+left({sqrt {-1}}ight)^{-1/3}ight).}$

На первый взгляд, это чушь. Однако формальные вычисления с комплексными числами показывают, что уравнение z³ = я есть решения −я, ${displaystyle { frac {sqrt {3}}{2}}+{ frac {i}{2}}}$ и ${displaystyle { frac {-{sqrt {3}}}{2}}+{ frac {i}{2}}}$. Подставляя их по очереди на ${displaystyle {{sqrt {-1}}^{1/3}}}$ в кубической формуле Тартальи и упрощении, можно получить 0, 1 и −1 как решения Икс³ − Икс = 0. Конечно, это конкретное уравнение можно решить с первого взгляда, но оно показывает, что, когда общие формулы используются для решения кубических уравнений с действительными корнями, тогда, как неукоснительно показали более поздние математики,^[22] использование комплексных чисел неизбежен. Рафаэль Бомбелли был первым, кто явно обратился к этим, казалось бы, парадоксальным решениям кубических уравнений, и разработал правила сложной арифметики, пытаясь разрешить эти проблемы.

Термин «мнимые» для этих величин был введен Рене Декарт в 1637 году, хотя он изо всех сил старался подчеркнуть их воображаемую природу^[23]

[...] иногда только воображаемый, то есть можно представить столько, сколько я сказал в каждом уравнении, но иногда не существует количества, которое соответствует тому, что мы представляем.([...] quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune Quantité qui correde à celle qu представьте себе.)

Еще одним источником путаницы было то, что уравнение ${displaystyle {sqrt {-1}}^{2}={sqrt {-1}}{sqrt {-1}}=-1}$ казался капризным несовместимым с алгебраическим тождеством ${displaystyle {sqrt {a}}{sqrt {b}}={sqrt {ab}}}$, что справедливо для неотрицательных действительных чисел а и б, и который также использовался в вычислениях комплексных чисел с одним из а, б положительный и другой отрицательный. Неправильное использование этого удостоверения (и связанного с ним удостоверения ${displaystyle { frac {1}{sqrt {a}}}={sqrt { frac {1}{a}}}}$) в случае, когда оба а и б отрицательны даже озадаченный Эйлером. Эта трудность в конечном итоге привела к соглашению использовать специальный символ я на месте √−1 чтобы избежать этой ошибки.^{[нужна цитата ]} Тем не менее, Эйлер считал естественным знакомить студентов с комплексными числами намного раньше, чем мы делаем это сегодня. В своем учебнике элементарной алгебры Элементы алгебры, он вводит эти числа почти сразу, а затем естественным образом использует их повсюду.

В 18 веке комплексные числа получили более широкое распространение, поскольку было замечено, что формальные манипуляции со сложными выражениями могут использоваться для упрощения вычислений с использованием тригонометрических функций. Например, в 1730 г. Абрахам де Муавр отметил, что сложные тождества, связывающие тригонометрические функции целого кратного угла со степенями тригонометрических функций этого угла, могут быть просто перевыражены следующей хорошо известной формулой, которая носит его имя: формула де Муавра:

${displaystyle (cos heta +isin heta )^{n}=cos n heta +isin n heta .}$

В 1748 г. Леонард Эйлер пошел дальше и получил Формула Эйлера из комплексный анализ:^[24]

${displaystyle cos heta +isin heta =e^{i heta }}$

формально манипулируя сложными степенной ряд и заметил, что эту формулу можно использовать для сведения любого тригонометрического тождества к гораздо более простым экспоненциальным тождествам.

Представление о комплексном числе как о точке на комплексной плоскости (над ) был впервые описан Каспар Вессель в 1799 г.,^[25] хотя это ожидалось еще в 1685 году в Уоллис Трактат по алгебре.^[26]

Мемуары Весселя опубликованы в журнале Proceedings of the Копенгагенская академия но остались незамеченными. В 1806 г. Жан-Робер Арган независимо выпустил брошюру по комплексным числам и предоставил строгое доказательство основная теорема алгебры.^[27] Карл Фридрих Гаусс ранее опубликовал существенно топологический доказательство теоремы в 1797 году, но выразил свои сомнения в то время относительно «истинной метафизики квадратного корня из -1».^[28] Только в 1831 году он преодолел эти сомнения и опубликовал свой трактат о комплексных числах как точках на плоскости.^[29][30] в основном устанавливают современные обозначения и терминологию.

Если раньше кто-то рассматривал этот предмет с ложной точки зрения и, следовательно, обнаружил таинственную тьму, то это в значительной степени связано с неуклюжей терминологией. Если бы кто-то не назвал +1, −1, √ − 1 положительными, отрицательными или воображаемыми (или даже невозможными) единицами, а вместо этого, скажем, прямыми, обратными или боковыми единицами, то вряд ли можно было бы говорить о такой темноте. - Гаусс^[29][30]

В начале 19 века другие математики независимо открыли геометрическое представление комплексных чисел: Буэ,^[31][32] Мурей,^[33] Уоррен,^[34] Français и его брат, Беллавит.^[35][36]

Английский математик G.H. Харди отметил, что Гаусс был первым математиком, который использовал комплексные числа «действительно уверенным и научным способом», хотя такие математики, как Нильс Хенрик Абель и Карл Густав Джейкоб Якоби обязательно использовали их регулярно до того, как Гаусс опубликовал свой трактат 1831 года.^[37]

Огюстен Луи Коши и Бернхард Риманн вместе объединил фундаментальные идеи комплексный анализ до высокой степени завершенности, начиная примерно с 1825 года в случае Коши.

Общие термины, используемые в теории, в основном принадлежат основателям. Арган позвонил ${displaystyle cos phi +isin phi }$ то фактор направления, и ${displaystyle r={sqrt {a^{2}+b^{2}}}}$ то модуль;^[38] Коши (1821) называл ${displaystyle cos phi +isin phi }$ то уменьшенная форма (l'expression réduite)^[39] и, видимо, ввел термин аргумент; Гаусс использовал я за ${displaystyle {sqrt {-1}}}$,^[40] ввел термин комплексное число за а + би,^[41] и позвонил а² + б² то норма.^[42] Выражение коэффициент направления, часто используется для ${displaystyle cos phi +isin phi }$, принадлежит Ганкелю (1867 г.),^[43] и абсолютная величина, за модуль, принадлежит Вейерштрассу.

Более поздние классические авторы по общей теории включают Ричард Дедекинд, Отто Гёльдер, Феликс Кляйн, Анри Пуанкаре, Герман Шварц, Карл Вейерштрасс и много других.

Отношения и операции

Равенство

Комплексные числа имеют такое же определение равенства, что и действительные числа; два комплексных числа ${displaystyle a_{1}+b_{1}i}$ и ${displaystyle a_{2}+b_{2}i}$ равны если и только если обе их действительная и мнимая части равны, то есть если ${displaystyle a_{1}=a_{2}}$ и ${displaystyle b_{1}=b_{2}}$. Ненулевые комплексные числа, записанные в полярная форма равны тогда и только тогда, когда они имеют одинаковую величину и их аргументы различаются на целое число, кратное 2π.

Заказ

В отличие от действительных чисел, комплексные числа не упорядочиваются естественным образом. В частности, поскольку комплексные числа естественным образом считаются существующими на двумерной плоскости, нет линейный порядок на комплексных числах, которые совместимы со сложением и умножением - комплексные числа не могут иметь структуру упорядоченное поле. Это потому, что любой квадрат в упорядоченном поле не меньше 0, но я² = −1.

Конъюгировать

Смотрите также: Комплексное сопряжение

Геометрическое представление z и его сопряженный z в комплексной плоскости

В комплексно сопряженный комплексного числа z = Икс + йи дан кем-то Икс − йи. Обозначается либо z или же z*.^[44] Этот унарная операция на комплексных числах нельзя выразить, применяя только их базовые операции сложения, вычитания, умножения и деления.

Геометрически, z это "отражение" из z о реальной оси. Двойное спряжение дает исходное комплексное число

${displaystyle {overline {overline {z}}}=z,}$

что делает эту операцию инволюция. Отражение оставляет как действительную часть, так и величину z без изменений, то есть

${displaystyle operatorname {Re} ({overline {z}})=operatorname {Re} (z)quad }$ и ${displaystyle quad |{overline {z}}|=|z|.}$

Мнимая часть и аргумент комплексного числа z менять знак при спряжении

${displaystyle operatorname {Im} ({overline {z}})=-operatorname {Im} (z)quad }$ и ${displaystyle quad operatorname {arg} ({overline {z}})equiv -operatorname {arg} (z){pmod {2pi }}.}$

Подробнее о аргументах и ​​величине см. Раздел Полярная форма.

Произведение комплексного числа ${displaystyle z=x+yi}$ и его конъюгат известен как абсолютный квадрат. Это всегда положительное действительное число, равное квадрату величины каждого:

${displaystyle zcdot {overline {z}}=x^{2}+y^{2}=|z|^{2}=|{overline {z}}|^{2}.}$

Это свойство можно использовать для преобразования дроби со сложным знаменателем в эквивалентную дробь с действительным знаменателем путем расширения числителя и знаменателя дроби на сопряжение данного знаменателя. Этот процесс иногда называют "рационализация "знаменателя (хотя знаменатель в конечном выражении может быть иррациональным действительным числом), поскольку он напоминает метод удаления корней из простых выражений в знаменателе.

Действительная и мнимая части комплексного числа z можно извлечь с помощью спряжения:

${displaystyle operatorname {Re} (z)={dfrac {z+{overline {z}}}{2}},quad }$ и ${displaystyle quad operatorname {Im} (z)={dfrac {z-{overline {z}}}{2i}}.}$

Более того, комплексное число реально тогда и только тогда, когда оно равно своему собственному сопряженному.

Сопряжение распределяет по основным сложным арифметическим операциям:

${displaystyle {overline {zpm w}}={overline {z}}pm {overline {w}},}$

${displaystyle {overline {zcdot w}}={overline {z}}cdot {overline {w}},quad {overline {z/w}}={overline {z}}/{overline {w}}.}$

Конъюгация также используется в инверсивная геометрия, раздел геометрии, изучающий более общие отражения, чем отражения от линии. в сетевой анализ электрических цепей, комплексное сопряжение используется для нахождения эквивалентного импеданса, когда теорема о передаче максимальной мощности ищется.

Сложение и вычитание

Сложить два комплексных числа можно геометрически, построив параллелограмм.

Два комплексных числа ${displaystyle a}$ и ${displaystyle b}$ легче всего добавлен добавляя по отдельности их действительную и мнимую части слагаемых. То есть:

${displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}$

По аналогии, вычитание может быть выполнен как

${displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}$

Используя визуализацию комплексных чисел на комплексной плоскости, сложение имеет следующую геометрическую интерпретацию: сумма двух комплексных чисел ${displaystyle a}$ и ${displaystyle b}$, интерпретируемая как точки на комплексной плоскости, является точкой, полученной путем построения параллелограмм из трех вершин ${displaystyle O}$, а точки стрелок ${displaystyle a}$ и ${displaystyle b}$ (при условии, что они не на линии). Точно так же, называя эти точки ${displaystyle A,;B,}$ соответственно и четвертая точка параллелограмма ${displaystyle X,}$ то треугольники ${displaystyle OAB}$ и ${displaystyle XBA}$ находятся конгруэнтный. Визуализации вычитания можно добиться, добавив отрицательные вычитаемое.

Умножение

Поскольку действительная часть, мнимая часть и неопределенная часть я в комплексном числе все рассматриваются как числа сами по себе, два комплексных числа, заданные как ${displaystyle z=x+yi}$ и ${displaystyle w=u+vi}$ умножаются по правилам распределительное свойство, то коммутативные свойства и определяющее свойство ${displaystyle i^{2}=-1}$ следующим образом

${displaystyle {egin{aligned}zcdot w&=(x+yi)cdot (u+vi)&&=x(u+vi)+yi(u+vi)&&{ ext{by the (right) distributive law}}&=xu+xvi+yiu+yivi&&{ ext{by the (left) distributive law}}&=xu+yivi+xvi+yiu&&{ ext{by the commutativity of addition}}&=xu+yvi^{2}+xvi+yui&&{ ext{by the commutativity of multiplication}}&=(xu+yvi^{2})+(xvi+yui)&&{ ext{by the associativity of addition}}&=(xu-yv)+(xvi+yui)&&{ ext{by the defining property of }}i&=(xu-yv)+(xv+yu)i&&{ ext{by the distributive law}}.end{aligned}}}$

Взаимное и деление

Используя спряжение, взаимный ненулевого комплексного числа z = Икс + йи всегда можно разбить на

${displaystyle {frac {1}{z}}={frac {overline {z}}{z{overline {z}}}}={frac {overline {z}}{|z|^{2}}}={frac {overline {z}}{x^{2}+y^{2}}}={frac {x}{x^{2}+y^{2}}}-{frac {y}{x^{2}+y^{2}}}i,}$

поскольку ненулевой подразумевает, что ${displaystyle x^{2}+y^{2}}$ больше нуля.

Это можно использовать для выражения деления произвольного комплексного числа. ${displaystyle w=u+vi}$ ненулевым комплексным числом ${displaystyle z}$ в качестве

${displaystyle {frac {w}{z}}=wcdot {frac {1}{z}}=(u+vi)cdot left({frac {x}{x^{2}+y^{2}}}-{frac {y}{x^{2}+y^{2}}}iight)={frac {1}{x^{2}+y^{2}}}left((ux+vy)+(vx-uy)iight).}$

Умножение и деление в полярной форме

Умножение 2 + я (синий треугольник) и 3 + я (красный треугольник). Красный треугольник поворачивается до вершины синего и растягивается на √5, длина гипотенуза синего треугольника.

Формулы для умножения, деления и возведения в степень проще в полярной форме, чем соответствующие формулы в декартовых координатах. Учитывая два комплексных числа z₁ = р₁(cos φ₁ + я грех φ₁) и z₂ = р₂(cos φ₂ + я грех φ₂), в силу тригонометрических тождеств

${displaystyle cos(a)cos(b)-sin(a)sin(b)=cos(a+b)}$

${displaystyle cos(a)sin(b)+sin(a)cos(b)=sin(a+b)}$

мы можем получить

${displaystyle z_{1}z_{2}=r_{1}r_{2}(cos(varphi _{1}+varphi _{2})+isin(varphi _{1}+varphi _{2})).}$

Другими словами, абсолютные значения умножаются, а аргументы складываются, чтобы получить полярную форму продукта. Например, умножая на я соответствует четвертиповернуть против часовой стрелки, что возвращает я² = −1. Картинка справа иллюстрирует умножение

${displaystyle (2+i)(3+i)=5+5i.}$

Поскольку реальная и мнимая часть 5 + 5я равны, аргумент этого числа равен 45 градусов, или π / 4 (в радиан ). С другой стороны, это также сумма углов в начале координат красного и синего треугольников. арктан (1/3) и arctan (1/2) соответственно. Таким образом, формула

${displaystyle {frac {pi }{4}}=arctan left({frac {1}{2}}ight)+arctan left({frac {1}{3}}ight)}$

держит. Поскольку арктан функция может быть аппроксимирована очень эффективно, такие формулы, известные как Машинные формулы - используются для высокоточных приближений π.

Точно так же деление дается

${displaystyle {frac {z_{1}}{z_{2}}}={frac {r_{1}}{r_{2}}}left(cos(varphi _{1}-varphi _{2})+isin(varphi _{1}-varphi _{2})ight).}$

Квадратный корень

Смотрите также: Квадратные корни из отрицательных и комплексных чисел

Квадратные корни из а + би (с б ≠ 0) находятся ${displaystyle pm (gamma +delta i)}$, куда

${displaystyle gamma ={sqrt {frac {a+{sqrt {a^{2}+b^{2}}}}{2}}}}$

и

${displaystyle delta =operatorname {sgn}(b){sqrt {frac {-a+{sqrt {a^{2}+b^{2}}}}{2}}},}$

где sgn - это сигнум функция. Это можно увидеть, возведя в квадрат ${displaystyle pm (gamma +delta i)}$ чтобы получить а + би.^[45][46] Здесь ${displaystyle {sqrt {a^{2}+b^{2}}}}$ называется модуль из а + би, а знак квадратного корня указывает на квадратный корень с неотрицательной действительной частью, называемый главный квадратный корень; также ${displaystyle {sqrt {a^{2}+b^{2}}}={sqrt {z{overline {z}}}},}$ куда ${displaystyle z=a+bi.}$^[47]

Экспоненциальная функция

В экспоненциальная функция ${displaystyle exp(z)}$ можно определить для каждого комплексного числа z посредством степенной ряд

${displaystyle exp z=sum _{n=0}^{infty }{frac {z^{n}}{n!}},}$

который имеет бесконечное радиус схождения.

Стоимость на 1 экспоненциальной функции Число Эйлера

${displaystyle e=exp 1=sum _{n=0}^{infty }{frac {1}{n!}}approx 2.71828.}$

Если z реально, есть ${displaystyle exp z=e^{z}.}$Аналитическое продолжение позволяет распространить это равенство на любое комплексное значение z, и, таким образом, определить комплексное возведение в степень с основанием е в качестве

${displaystyle e^{z}=exp z.}$

Функциональное уравнение

Показательная функция удовлетворяет функциональное уравнение${displaystyle e^{z+t}=e^{z}e^{t}.}$Это можно доказать либо путем сравнения разложения обоих элементов в степенной ряд, либо путем применения аналитическое продолжение от ограничения уравнения действительными аргументами.

Формула Эйлера

Формула Эйлера утверждает, что для любого действительного числа Икс,

${displaystyle e^{ix}=cos x+isin x.}$

Таким образом, из функционального уравнения следует, что если Икс и у реальны, есть

${displaystyle e^{x+iy}=e^{x}(cos y+isin y),}$

которая представляет собой разложение экспоненциальной функции на действительную и мнимую части.

Возведение в степень

Если Икс > 0 реально и z комплексное возведение в степень определяется как

${displaystyle x^{z}=e^{zln x},}$

куда пер обозначает натуральный логарифм.

Представляется естественным распространить эту формулу на комплексные значения Икс, но есть некоторые трудности, связанные с тем, что комплексный логарифм на самом деле не функция, а многозначная функция.

Комплексный логарифм

В реальном случае натуральный логарифм можно определить как обратный экспоненциальной функции. Чтобы распространить это на комплексную область, можно начать с формулы Эйлера. Это означает, что если комплексное число z написано в полярная форма

${displaystyle z=r(cos varphi +isin varphi ),}$

тогда это комплексный логарифм должно быть

${displaystyle ln(z)=ln(r)+varphi i.}$

Однако, поскольку косинус и синус являются периодическими функциями, добавление к ${displaystyle varphi }$ целого кратного 2π. не меняется z. Например, ${displaystyle e^{ipi }=e^{3ipi }=-1}$так что оба ${displaystyle ipi }$ и ${displaystyle 3ipi }$ возможные значения натурального логарифма ${displaystyle -1}$.

Следовательно, комплексный логарифм должен быть определен как многозначная функция:

${displaystyle ln(z)=left{ln(r)+varphi i+2pi kimid kin mathbb {Z} ight}.}$

В качестве альтернативы срезанная ветка может использоваться для определения истинной функции. Если z не отрицательное действительное число, основная стоимость комплексного логарифма получается с помощью ${displaystyle -pi <varphi <pi .}$ Это аналитическая функция вне отрицательных действительных чисел, но его нельзя продолжить до функции, которая является непрерывной при любом отрицательном действительном числе.

Отсюда следует, что если z как указано выше, и если т - другое комплексное число, тогда возведение в степень многозначная функция

${displaystyle z^{t}=left{e^{tln r},(cos(varphi t+2pi kt)+isin(varphi t+2pi kt))}mid kin mathbb {Z} ight}}$

Целые и дробные показатели

Геометрическое представление корней 2–6 комплексного числа z, в полярной форме повторно^iφ  куда р = |z | и φ = arg z. Если z реально, φ = 0 или π. Основные корни показаны черным.

Если в предыдущей формуле т является целым числом, то синус и косинус не зависят от k. Таким образом, если показатель степени п целое число, тогда ${displaystyle z^{n}}$ хорошо определена, и формула возведения в степень упрощается до формула де Муавра:

${displaystyle z^{n}=(r(cos varphi +isin varphi ))^{n}=r^{n},(cos nvarphi +isin nvarphi ).}$

В п пкорни комплексного числа z даны

${displaystyle z^{1/n}={sqrt[{n}]{r}}left(cos left({frac {varphi +2kpi }{n}}ight)+isin left({frac {varphi +2kpi }{n}}ight)ight)}$

за 0 ≤ k ≤ п − 1. (Здесь ${displaystyle {sqrt[{n}]{r}}}$ обычный (положительный) пкорень -й положительного действительного числа р.) Поскольку синус и косинус периодичны, другие целые значения k не дают других значений.

В то время как пкорень -й степени положительного действительного числа р выбран, чтобы быть положительный настоящий номер c удовлетворение c^п = р, нет естественного способа выделить один конкретный комплекс пкорень -й степени комплексного числа. Следовательно пй корень п-значная функция из z. Это означает, что, в отличие от положительных действительных чисел,

${displaystyle (z^{n})^{1/n}eq z,}$

так как левая часть состоит из п values, а правая часть - одно значение.

Характеристики

Структура поля

Набор C комплексных чисел - это поле.^[48] Вкратце, это означает, что верны следующие факты: во-первых, любые два комплексных числа можно сложить и умножить, чтобы получить другое комплексное число. Во-вторых, для любого комплексного числа z, это Противоположное число −z тоже комплексное число; в-третьих, каждое ненулевое комплексное число имеет взаимный комплексное число. Более того, эти операции удовлетворяют ряду законов, например закону коммутативность сложения и умножения любых двух комплексных чисел z₁ и z₂:

${displaystyle z_{1}+z_{2}=z_{2}+z_{1},}$

${displaystyle z_{1}z_{2}=z_{2}z_{1}.}$

Эти два закона и другие требования к полю можно доказать с помощью приведенных выше формул, используя тот факт, что действительные числа сами по себе образуют поле.

В отличие от реалов, C не является упорядоченное поле, то есть невозможно определить отношение z₁ < z₂ это совместимо со сложением и умножением. Фактически, в любом упорядоченном поле квадрат любого элемента обязательно положителен, поэтому я² = −1 исключает существование заказ на C.^[49]

Когда базовым полем математической темы или конструкции является поле комплексных чисел, название темы обычно изменяется, чтобы отразить этот факт. Например: комплексный анализ, сложный матрица, сложный многочлен, и сложный Алгебра Ли.

Решения полиномиальных уравнений

Учитывая любые комплексные числа (называемые коэффициенты ) а₀, ..., а_п, уравнение

${displaystyle a_{n}z^{n}+dotsb +a_{1}z+a_{0}=0}$

имеет хотя бы одно комплексное решение zпри условии, что хотя бы один из старших коэффициентов а₁, ..., а_п не равно нулю.^[50] Это заявление основная теорема алгебры, из Карл Фридрих Гаусс и Жан ле Ронд д'Аламбер. Из-за этого C называется алгебраически замкнутое поле. Это свойство не выполняется для поле рациональных чисел Q (полином Икс² − 2 не имеет рационального корня, так как √2 не рациональное число), ни действительные числа р (полином Икс² + а не имеет настоящего корня для а > 0, так как квадрат Икс положительно для любого действительного числа Икс).

Существуют различные доказательства этой теоремы аналитическими методами, такими как Теорема Лиувилля, или же топологический такие как номер намотки, или доказательство, объединяющее Теория Галуа и тот факт, что любой действительный многочлен от странный Степень имеет хотя бы один настоящий корень.

По этой причине справедливые теоремы для любого алгебраически замкнутого поля применить к C. Например, любой непустой комплекс квадратная матрица имеет хотя бы один (сложный) собственное значение.

Алгебраическая характеристика

Поле C имеет следующие три свойства: во-первых, он имеет характеристика 0. Это означает, что 1 + 1 + ⋯ + 1 ≠ 0 для любого количества слагаемых (все равны одному). Во-вторых, это степень превосходства над Q, то основное поле из C, это мощность континуума. В-третьих, это алгебраически замкнутый (см. выше). Можно показать, что любое поле, обладающее этими свойствами, является изоморфный (как поле) в C. Например, алгебраическое замыкание из Q_п также удовлетворяет этим трем свойствам, поэтому эти два поля изоморфны (как поля, но не как топологические поля).^[51] Также, C изоморфно полю комплексных Серия Puiseux. Однако для задания изоморфизма требуется аксиома выбора. Другое следствие этой алгебраической характеристики состоит в том, что C содержит много собственных подполей, изоморфных C.

Характеризация как топологическое поле

Предыдущая характеристика C описывает только алгебраические аспекты C. То есть свойства близость и непрерывность, что имеет значение в таких областях, как анализ и топология, не рассматриваются. Следующее описание C как топологическое поле (то есть поле, снабженное топология, что допускает понятие сходимости) учитывает топологические свойства. C содержит подмножество п (а именно набор положительных действительных чисел) ненулевых элементов, удовлетворяющих следующим трем условиям:

• п замкнута относительно сложения, умножения и взятия обратных.
• Если Икс и у являются отдельными элементами п, то либо Икс − у или же у − Икс в п.
• Если S есть любое непустое подмножество п, тогда S + п = Икс + п для некоторых Икс в C.

Более того, C имеет нетривиальный инволютивный автоморфизм Икс ↦ Икс* (а именно комплексное сопряжение), такое что х х* в п для любого ненулевого Икс в C.

Любое поле F с этими свойствами можно наделить топологией, взяв множества B(Икс, п) = { у | п − (у − Икс)(у − Икс)* ∈ п }  как основание, куда Икс колеблется по полю и п колеблется над п. С этой топологией F изоморфен как топологический поле для C.

Единственный связаны локально компактный топологические поля находятся р и C. Это дает другую характеристику C как топологическое поле, поскольку C можно отличить от р потому что ненулевые комплексные числа связаны, а ненулевые действительные числа - нет.^[52]

Формальное строительство

Строительство в виде заказанных пар

Уильям Роуэн Гамильтон представил подход к определению множества C комплексных чисел^[53] как набор р² из заказанные пары (а, б) действительных чисел, в которых действуют следующие правила сложения и умножения:^[48]

${displaystyle {egin{aligned}(a,b)+(c,d)&=(a+c,b+d)(a,b)cdot (c,d)&=(ac-bd,bc+ad).end{aligned}}}$

В этом случае для выражения (а, б) в качестве а + би.

Строительство как поле частного

Хотя эта низкоуровневая конструкция действительно точно описывает структуру комплексных чисел, следующее эквивалентное определение раскрывает алгебраическую природу C больше сразу. Эта характеристика основана на понятии полей и многочленов. Поле - это набор, наделенный операциями сложения, вычитания, умножения и деления, которые ведут себя так же, как, например, по рациональным числам. Например, распределительный закон

${displaystyle (x+y)z=xz+yz}$

должен выполняться для любых трех элементов Икс, у и z поля. Набор р действительных чисел действительно образует поле. Полином п(Икс) с реальным коэффициенты является выражением формы

${displaystyle a_{n}X^{n}+dotsb +a_{1}X+a_{0},}$

где а₀, ..., а_п настоящие числа. Обычное сложение и умножение многочленов дает множество р[Икс] всех таких многочленов с звенеть структура. Это кольцо называется кольцо многочленов над реальными числами.

Набор комплексных чисел определяется как кольцо частного р[Икс]/(Икс ² + 1).^[6] Это поле расширения содержит два квадратных корня из −1, а именно ( смежные классы из) Икс и −Икс, соответственно. (Смежные классы) 1 и Икс составляют основу р[Икс]/(Икс ² + 1) как настоящий векторное пространство, что означает, что каждый элемент поля расширения может быть однозначно записан как линейная комбинация в этих двух элементах. Эквивалентно, элементы поля расширения могут быть записаны как упорядоченные пары (а, б) реальных чисел. Фактор-кольцо - это поле, потому что Икс² + 1 является несводимый над р, поэтому идеал, который он генерирует, максимальный.

Формулы сложения и умножения в кольце р[Икс], по модулю отношения Икс² = −1, соответствуют формулам сложения и умножения комплексных чисел, определенных как упорядоченные пары. Итак, два определения поля C находятся изоморфный (как поля).

Принимая это C алгебраически замкнуто, так как это алгебраическое расширение из р в этом подходе C поэтому алгебраическое замыкание из р.

Матричное представление комплексных чисел

Сложные числа а + би также может быть представлен 2 × 2 матрицы которые имеют следующий вид:

${displaystyle {egin{pmatrix}a&-b&;;aend{pmatrix}}}$

Здесь записи а и б настоящие числа. Сумма и произведение двух таких матриц снова имеют такую ​​форму, а сумма и произведение комплексных чисел соответствует сумме и товар таких матриц, продукт:

${displaystyle {egin{pmatrix}a&-b&;;aend{pmatrix}}{egin{pmatrix}c&-dd&;;cend{pmatrix}}={egin{pmatrix}ac-bd&-ad-bcc+ad&;;-bd+acend{pmatrix}}}$

Геометрическое описание умножения комплексных чисел также может быть выражено в терминах матрицы вращения используя это соответствие между комплексными числами и такими матрицами. Более того, квадрат абсолютного значения комплексного числа, выраженного в виде матрицы, равен детерминант этой матрицы:

${displaystyle |z|^{2}={egin{vmatrix}a&-b&aend{vmatrix}}=a^{2}+b^{2}.}$

Сопряженный ${displaystyle {overline {z}}}$ соответствует транспонировать матрицы.

Хотя это представление комплексных чисел с матрицами является наиболее распространенным, многие другие представления возникают из матриц Кроме как ${displaystyle {igl (}{egin{smallmatrix}0&-11&0end{smallmatrix}}{igr )}}$ этот квадрат к отрицанию единичная матрица. См. Статью о 2 × 2 вещественные матрицы для других представлений комплексных чисел.

Комплексный анализ

График цветового круга из грех (1 /z). Черные части внутри относятся к числам, имеющим большие абсолютные значения.

Основная статья: Комплексный анализ

Изучение функций комплексного переменного известно как комплексный анализ и имеет огромное практическое применение в Прикладная математика а также в других разделах математики. Часто наиболее естественные доказательства утверждений в реальный анализ или даже теория чисел использовать методы комплексного анализа (см. теорема о простых числах для примера). В отличие от реальных функций, которые обычно представляют в виде двумерных графиков, сложные функции имеют четырехмерные графики и могут быть с пользой проиллюстрированы с помощью цветного кодирования трехмерный график предложить четыре измерения, или путем анимации динамического преобразования сложной функции комплексной плоскости.

Сложные экспоненциальные и связанные функции

Представления о сходящийся ряд и непрерывные функции в (реальном) анализе имеют естественные аналоги в комплексном анализе. Последовательность комплексных чисел называется сходиться тогда и только тогда, когда есть его реальная и мнимая части. Это эквивалентно (ε, δ) -определение пределов, где модуль действительных чисел заменен на модуль комплексных чисел. С более абстрактной точки зрения, C, наделенный метрика

${displaystyle operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|}$

это полный метрическое пространство, который, в частности, включает неравенство треугольника

${displaystyle |z_{1}+z_{2}|leq |z_{1}|+|z_{2}|}$

для любых двух комплексных чисел z₁ и z₂.

Как и в реальном анализе, это понятие сходимости используется для построения ряда элементарные функции: the экспоненциальная функция exp z, также написано е^z, определяется как бесконечная серия

${displaystyle exp z:=1+z+{frac {z^{2}}{2cdot 1}}+{frac {z^{3}}{3cdot 2cdot 1}}+cdots =sum _{n=0}^{infty }{frac {z^{n}}{n!}}.}$

Ряд, определяющий действительные тригонометрические функции синус и косинус, так же хорошо как гиперболические функции sinh и cosh также без изменений переносятся на сложные аргументы. Для других тригонометрических и гиперболических функций, таких как касательная, все немного сложнее, так как определяющие ряды не сходятся для всех комплексных значений. Следовательно, их следует определять либо в терминах синуса, косинуса и экспоненты, либо, что то же самое, с помощью метода аналитическое продолжение.

Формула Эйлера состояния:

${displaystyle exp(ivarphi )=cos varphi +isin varphi }$

для любого реального числа φ, особенно

${displaystyle exp(ipi )=-1}$

В отличие от ситуации с действительными числами, существует бесконечность комплексных решений z уравнения

${displaystyle exp z=w}$

для любого комплексного числа ш ≠ 0. Можно показать, что любое такое решение z - называется комплексный логарифм из ш - удовлетворяет

${displaystyle log w=ln |w|+iarg w,}$

где arg - это аргумент определенный над, и в (реальном) натуральный логарифм. Поскольку arg является многозначная функция, уникальность только до кратного 2π, журнал тоже многозначен. В основная стоимость бревна часто берется путем ограничения мнимой части до интервал (−π, π].

Сложный возведение в степень z^ω определяется как

${displaystyle z^{omega }=exp(omega log z),}$

и многозначен, кроме случаев, когда ${displaystyle omega }$ целое число. За ω = 1 / п, для некоторого натурального числа п, это восстанавливает неединственность пупомянутые выше корни.

Комплексные числа, в отличие от действительных чисел, в общем случае не удовлетворяют неизменным тождествам степени и логарифма, особенно когда их наивно трактуют как однозначные функции; видеть отказ от тождества мощности и логарифма. Например, они не удовлетворяют

${displaystyle a^{bc}=left(a^{b}ight)^{c}.}$

Обе части уравнения многозначны в соответствии с определением комплексного возведения в степень, данным здесь, а значения слева являются подмножеством значений справа.

Голоморфные функции

Функция ж : C → C называется голоморфный если он удовлетворяет Уравнения Коши – Римана. Например, любой р-линейный карта C → C можно записать в виде

${displaystyle f(z)=az+b{overline {z}}}$

с комплексными коэффициентами а и б. Это отображение голоморфно если и только если б = 0. Второе слагаемое ${displaystyle b{overline {z}}}$ действительно дифференцируема, но не удовлетворяет Уравнения Коши – Римана.

Комплексный анализ показывает некоторые особенности, не очевидные при реальном анализе. Например, любые две голоморфные функции ж и грамм которые соглашаются на сколь угодно малые открытое подмножество из C обязательно везде соглашусь. Мероморфные функции, функции, которые можно локально записать как ж(z)/(z − z₀)^п с голоморфной функцией ж, по-прежнему обладают некоторыми чертами голоморфных функций. Другие функции имеют существенные особенности, Такие как грех (1 /z) в z = 0.

Приложения

Комплексные числа находят применение во многих научных областях, в том числе обработка сигналов, теория управления, электромагнетизм, динамика жидкостей, квантовая механика, картография, и анализ вибрации. Некоторые из этих приложений описаны ниже.

Геометрия

Формы

Три неколлинеарный точки ${displaystyle u,v,w}$ в самолете определить форма треугольника ${displaystyle {u,v,w}}$. Располагая точки на комплексной плоскости, эта форма треугольника может быть выражена комплексной арифметикой как

${displaystyle S(u,v,w)={frac {u-w}{u-v}}.}$

Форма ${displaystyle S}$ треугольника останется прежним, когда комплексная плоскость трансформируется путем сдвига или растяжения ( аффинное преобразование ), что соответствует интуитивному представлению о форме и описывает сходство. Таким образом, каждый треугольник ${displaystyle {u,v,w}}$ находится в класс сходства треугольников одинаковой формы.^[54]

Фрактальная геометрия

Набор Мандельброта с помеченными реальными и мнимыми осями.

В Набор Мандельброта - популярный пример фрактала, образованного на комплексной плоскости. Он определяется путем нанесения каждого местоположения ${displaystyle c}$ где итерация последовательности ${displaystyle f_{c}(z)=z^{2}+c}$ не расходиться когда повторяется бесконечно. По аналогии, Юля наборы имеют те же правила, кроме тех случаев, когда ${displaystyle c}$ остается постоянным.

Треугольники

Каждый треугольник имеет уникальный Штайнер инеллипс - ан эллипс внутри треугольника и касательная к серединам трех сторон треугольника. В фокусы эллипса Штейнера треугольника можно найти следующим образом, согласно Теорема мардена:^[55][56] Обозначим вершины треугольника на комплексной плоскости как а = Икс_А + у_Ая, б = Икс_B + у_Bя, и c = Икс_C + у_Cя. Написать кубическое уравнение ${displaystyle scriptstyle (x-a)(x-b)(x-c)=0}$, возьмите его производную и приравняйте (квадратичную) производную к нулю. Теорема Мардена говорит, что решениями этого уравнения являются комплексные числа, обозначающие положения двух фокусов эллипса Штейнера.

Алгебраическая теория чисел

Построение правильного пятиугольника с помощью линейки и компаса.

Как упоминалось выше, любое непостоянное полиномиальное уравнение (с комплексными коэффициентами) имеет решение в C. А тем более то же самое верно, если уравнение имеет рациональные коэффициенты. Корни таких уравнений называются алгебраические числа - они являются основным объектом изучения в алгебраическая теория чисел. В сравнении с Q, алгебраическое замыкание Q, который также содержит все алгебраические числа, C имеет то преимущество, что его легко понять с геометрической точки зрения. Таким образом, алгебраические методы могут использоваться для изучения геометрических вопросов и наоборот. С помощью алгебраических методов, более конкретно применяя механизм теория поля к числовое поле содержащий корни единства, можно показать, что построить регулярный девятиугольник используя только циркуль и линейку - чисто геометрическая задача.

Другой пример: Гауссовские целые числа, то есть числа вида Икс + иу, куда Икс и у целые числа, которые можно использовать для классификации суммы квадратов.

Аналитическая теория чисел

Основная статья: Аналитическая теория чисел

Аналитическая теория чисел изучает числа, часто целые или рациональные, используя тот факт, что их можно рассматривать как комплексные числа, в которых могут использоваться аналитические методы. Это делается путем кодирования теоретико-числовой информации в комплекснозначных функциях. Например, Дзета-функция Римана ζ (s) связано с распределением простые числа.

Несобственные интегралы

В прикладных областях комплексные числа часто используются для вычисления определенных действительных значений. несобственные интегралы, с помощью комплексных функций. Для этого существует несколько методов; видеть методы контурной интеграции.

Динамические уравнения

В дифференциальные уравнения, обычно сначала находят все сложные корни р из характеристическое уравнение из линейное дифференциальное уравнение или систему уравнений, а затем попытайтесь решить эту систему в терминах основных функций вида ж(т) = е^rt. Точно так же в разностные уравнения, сложные корни р характеристического уравнения системы разностных уравнений, чтобы попытаться решить систему в терминах базовых функций вида ж(т) = р^т.

В прикладной математике

Теория управления

В теория управления, системы часто трансформируются из область времени к частотная область с использованием Преобразование Лапласа. Система нули и полюсы затем анализируются в комплексная плоскость. В корневой локус, Сюжет Найквиста, и Заговор Николса все техники используют комплексную плоскость.

В методе корневого годографа важно, находятся ли нули и полюсы в левой или правой полуплоскостях, то есть имеют действительную часть больше или меньше нуля. Если линейная, инвариантная во времени (LTI) система имеет полюса, которые

• в правой полуплоскости будет неустойчивый,
• все в левой полуплоскости, это будет стабильный,
• на мнимой оси он будет иметь предельная стабильность.

Если система имеет нули в правой полуплоскости, это неминимальная фаза система.

Анализ сигналов

Комплексные числа используются в анализ сигналов и другие поля для удобного описания периодически меняющихся сигналов. Для заданных реальных функций, представляющих реальные физические величины, часто в терминах синусов и косинусов, рассматриваются соответствующие комплексные функции, действительные части которых являются исходными величинами. Для синусоидальная волна данного частота, абсолютное значение |z| соответствующих z это амплитуда и аргумент аргумент (z) это фаза.

Если Анализ Фурье используется для записи заданного действительного сигнала в виде суммы периодических функций, эти периодические функции часто записываются как комплексные функции вида

${displaystyle x(t)=operatorname {Re} {X(t)}}$

и

${displaystyle X(t)=Ae^{iomega t}=ae^{iphi }e^{iomega t}=ae^{i(omega t+phi )}}$

где ω представляет собой угловая частота и комплексное число А кодирует фазу и амплитуду, как описано выше.

Это использование также распространяется на цифровая обработка сигналов и цифровая обработка изображений, которые используют цифровые версии анализа Фурье (и вейвлет анализ) передавать, компресс, восстановить или иным образом обработать цифровой аудио сигналы, неподвижные изображения и видео сигналы.

Другой пример, относящийся к двум боковым полосам амплитудная модуляция AM радио, это:

${displaystyle {egin{aligned}cos((omega +alpha )t)+cos left((omega -alpha )tight)&=operatorname {Re} left(e^{i(omega +alpha )t}+e^{i(omega -alpha )t}ight)&=operatorname {Re} left(left(e^{ialpha t}+e^{-ialpha t}ight)cdot e^{iomega t}ight)&=operatorname {Re} left(2cos(alpha t)cdot e^{iomega t}ight)&=2cos(alpha t)cdot operatorname {Re} left(e^{iomega t}ight)&=2cos(alpha t)cdot cos left(omega tight).end{aligned}}}$

В физике

Электромагнетизм и электротехника

Основная статья: Переменный ток

В электротехника, то преобразование Фурье используется для анализа различных напряжения и токи. Лечение резисторы, конденсаторы, и индукторы затем могут быть объединены путем введения мнимых частотно-зависимых сопротивлений для последних двух и объединения всех трех в одно комплексное число, называемое сопротивление. Такой подход называется фазор исчисление.

В электротехнике мнимая единица обозначается как j, чтобы избежать путаницы с я, который обычно используется для обозначения электрический ток, или, более конкретно, я, который обычно используется для обозначения мгновенного электрического тока.

Поскольку Напряжение в AC схема колеблется, его можно представить как

${displaystyle V(t)=V_{0}e^{jomega t}=V_{0}left(cos omega t+jsin omega tight),}$

Для получения измеряемой величины берется действительная часть:

${displaystyle v(t)=mathrm {Re} (V)=mathrm {Re} left[V_{0}e^{jomega t}ight]=V_{0}cos omega t.}$

Комплекснозначный сигнал ${displaystyle V(t)}$ называется аналитический представление измеряемого сигнала с действительным знаком ${displaystyle v(t)}$.^[57]

Динамика жидкостей

В динамика жидкостей, сложные функции используются для описания потенциальный поток в двух измерениях.

Квантовая механика

Поле комплексных чисел присуще математические формулировки квантовой механики, где сложные Гильбертовы пространства предоставить контекст для одной такой формулировки, которая является удобной и, возможно, наиболее стандартной. Первоначальные формулы основы квантовой механики - Уравнение Шредингера и Гейзенберга матричная механика - используйте комплексные числа.

Относительность

В специальный и общая теория относительности, некоторые формулы для метрики на пространство-время станет проще, если принять временную составляющую пространственно-временного континуума как мнимую. (Этот подход больше не является стандартным в классической теории относительности, но используется существенно в квантовая теория поля.) Комплексные числа необходимы для спиноры, которые являются обобщением тензоры используется в теории относительности.

Обобщения и родственные понятия

График кватернионов Кэли Q8, показывающий циклы умножения на я, j и k

Процесс расширения поля р реалов на C известен как Конструкция Кэли-Диксона. Его можно перенести в более высокие измерения, давая кватернионы ЧАС и октонионы О которые (как реальное векторное пространство) имеют размерность 4 и 8, соответственно. В этом контексте комплексные числа были названы бинарионы.^[58]

Так же, как применяя конструкцию к реальным свойствам заказ теряется, свойства, известные по действительным и комплексным числам, исчезают с каждым расширением. В кватернионы теряют коммутативность, то есть Икс·у ≠ у·Икс для некоторых кватернионов Икс, у, и умножение октонионы, помимо того, что он не коммутативен, не может быть ассоциативным: (Икс·у)·z ≠ Икс·(у·z) для некоторых октонионов Икс, у, z.

Действительные числа, комплексные числа, кватернионы и октонионы - все это нормированные алгебры с делением над р. К Теорема Гурвица они единственные; то седенионы, следующий шаг в конструкции Кэли – Диксона, не имеют такой структуры.

Конструкция Кэли – Диксона тесно связана с регулярное представительство из C, задуманный как р-алгебра (ан р-векторное пространство с умножением) относительно базиса (1, я). Это означает следующее: р-линейная карта

${displaystyle {egin{aligned}mathbb {C} &ightarrow mathbb {C} z&mapsto wzend{aligned}}}$

для некоторого фиксированного комплексного числа ш может быть представлен 2 × 2 матрица (после выбора базиса). Что касается основы (1, я), эта матрица

${displaystyle {egin{pmatrix}operatorname {Re} (w)&-operatorname {Im} (w)operatorname {Im} (w)&operatorname {Re} (w)end{pmatrix}},}$

то есть тот, который упомянут в разделе о матричном представлении комплексных чисел выше. Пока это линейное представление из C в 2 × 2 вещественные матрицы, это не единственный. Любая матрица

${displaystyle J={egin{pmatrix}p&q &-pend{pmatrix}},quad p^{2}+qr+1=0}$

обладает тем свойством, что его квадрат является отрицанием единичной матрицы: J² = −я. потом

${displaystyle {z=aI+bJ:a,bin mathbf {R} }}$

также изоморфно полю C, и дает альтернативную сложную структуру на р². Это обобщается понятием линейная сложная структура.

Гиперкомплексные числа также обобщить р, C, ЧАС, и О. Например, это понятие содержит разделенные комплексные числа, которые являются элементами кольца р[Икс]/(Икс² − 1) (в отличие от р[Икс]/(Икс² + 1)). В этом кольце уравнение а² = 1 имеет четыре решения.

Поле р завершение Q, Поле рациональное число, относительно обычного абсолютная величина метрика. Другие варианты метрики на Q вести к полям Q_п из п-адические числа (для любого простое число п), которые тем самым аналогичны р. Других нетривиальных способов завершить Q чем р и Q_п, к Теорема Островского. Алгебраические замыкания ${displaystyle {overline {mathbf {Q} _{p}}}}$ из Q_п еще несут норму, но (в отличие от C) не полны по отношению к нему. Завершение ${displaystyle mathbf {C} _{p}}$ из ${displaystyle {overline {mathbf {Q} _{p}}}}$ оказывается алгебраически замкнутым. Это поле называется п-адические комплексные числа по аналогии.

Поля р и Q_п и их конечные расширения полей, включая C, находятся местные поля.

Смотрите также

• Алгебраическая поверхность
• Круговое движение с использованием комплексных чисел
• Комплексно-базовая система
• Сложная геометрия
• Двойное комплексное число
• Целое число Эйзенштейна
• Тождество Эйлера
• Геометрическая алгебра (который включает комплексную плоскость как двумерную спинор подпространство ${displaystyle {mathcal {G}}_{2}^{+}}$)
• Корень единства
• Комплексное число единицы

Примечания

1. Подробное описание истории, от первоначального скептицизма до окончательного признания, см.Бурбаки 1998 ), страницы 18-24.
2. В современных обозначениях решение Тартальи основано на расширении куба суммы двух кубических корней: ${displaystyle left({sqrt[{3}]{u}}+{sqrt[{3}]{v}}ight)^{3}=3{sqrt[{3}]{uv}}left({sqrt[{3}]{u}}+{sqrt[{3}]{v}}ight)+u+v}$ С ${displaystyle x={sqrt[{3}]{u}}+{sqrt[{3}]{v}}}$, ${displaystyle p=3{sqrt[{3}]{uv}}}$, ${displaystyle q=u+v}$, ты и v можно выразить через п и q в качестве ${displaystyle u=q/2+{sqrt {(q/2)^{2}-(p/3)^{3}}}}$ и ${displaystyle v=q/2-{sqrt {(q/2)^{2}-(p/3)^{3}}}}$, соответственно. Следовательно, ${displaystyle x={sqrt[{3}]{q/2+{sqrt {(q/2)^{2}-(p/3)^{3}}}}}+{sqrt[{3}]{q/2-{sqrt {(q/2)^{2}-(p/3)^{3}}}}}}$. Когда ${displaystyle (q/2)^{2}-(p/3)^{3}}$ отрицательна (casus unducibilis), второй кубический корень следует рассматривать как комплексное сопряжение первого.

Рекомендации

1. «Исчерпывающий список символов алгебры». Математическое хранилище. 25 марта 2020 г.. Получено 12 августа 2020.
2. Пенроуз, Роджер (2016). Дорога к реальности: полное руководство по законам Вселенной (перепечатано под ред.). Случайный дом. С. 72–73. ISBN  978-1-4464-1820-8. Выдержка из п. 73: «Комплексные числа, как и действительные, а может быть, даже больше, находят единство с природой, что поистине замечательно. Как будто сама природа впечатлена масштабом и последовательностью системы комплексных чисел, как и мы сами, и доверила этим числам точные операции своего мира в его мельчайших масштабах ».
3. "Сложные числа". www.mathsisfun.com. Получено 12 августа 2020.
4. "Комплексные числа | Блестящая вики по математике и науке". brilliant.org. Получено 12 августа 2020.
5. Бертон, Дэвид М. (1995), История математики (3-е изд.), Нью-Йорк: Макгроу-Хилл, п. 294, г. ISBN  978-0-07-009465-9
6. Бурбаки, Николас. «VIII.1». Общая топология. Springer-Verlag.
7. Акслер, Шелдон (2010). Колледж алгебра. Вайли. п.262.
8. Spiegel, M.R .; Lipschutz, S .; Schiller, J.J .; Спеллман, Д. (14 апреля 2009 г.), Комплексные переменные (2-е издание), Серия набросков Шаума, Макгроу Хилл, ISBN  978-0-07-161569-3
9. Aufmann, Ричард Н .; Баркер, Вернон С.; Нация, Ричард Д. (2007), "Глава П", Студенческая алгебра и тригонометрия (6-е изд.), Cengage Learning, стр. 66, ISBN  978-0-618-82515-8
10. Видеть (Альфорс 1979 ) ошибка harv: несколько целей (2 ×): CITEREFAhlfors1979 (помощь).
11. Браун, Джеймс Уорд; Черчилль, Руэль В. (1996), Сложные переменные и приложения (6-е изд.), Нью-Йорк: Макгроу-Хилл, стр. 2, ISBN  978-0-07-912147-9, В электротехнике буква j используется вместо я.
12. Педое, Дэн (1988), Геометрия: комплексный курс, Дувр, ISBN  978-0-486-65812-4
13. Видеть (Соломенцев 2001 ): «Плоскость $ R ^ 2 $, точки которой отождествляются с элементами $ C $, называется комплексной плоскостью» ... «Полная геометрическая интерпретация комплексных чисел и операций над ними впервые появилась в работе C. Вессель (1799 г.). Геометрическое представление комплексных чисел, иногда называемое «диаграммой Аргана», вошло в употребление после публикации в 1806 и 1814 гг. Работ Дж. Р. Аргана, который заново открыл, в значительной степени независимо, результаты Весселя ».
14. Вайсштейн, Эрик В. "Комплексное число". mathworld.wolfram.com. Получено 12 августа 2020.
15. Видеть (Апостол 1981 г. ), стр.18.
16. Касана, Х.С. (2005), "Глава 1", Комплексные переменные: теория и приложения (2-е изд.), PHI Learning Pvt. ООО, п. 14, ISBN  978-81-203-2641-5
17. Нильссон, Джеймс Уильям; Ридель, Сьюзан А. (2008), «Глава 9», Электрические схемы (8-е изд.), Прентис Холл, стр. 338, г. ISBN  978-0-13-198925-2
18. Клайн, Моррис. История математической мысли, том 1. п. 253.
19. Кац, Виктор Дж. (2004), «9.1.4», История математики, краткая версия, Эддисон-Уэсли, ISBN  978-0-321-16193-2
20. Гамильтон, Wm. (1844 г.). «О новом виде мнимых величин, связанных с теорией кватернионов». Труды Королевской ирландской академии. 2: 424–434.
21. Нахин, Пол Дж. (2007), Воображаемая сказка: История √−1, Princeton University Press, ISBN  978-0-691-12798-9, в архиве из оригинала 12 октября 2012 г., получено 20 апреля 2011
22. Конфалониери, Сара (2015). Недостижимая попытка избежать Casus Irreducibilis для кубических уравнений: De Regula Aliza Джероламо Кардано. Springer. С. 15–16 (примечание 26). ISBN  978-3658092757. Было доказано, что мнимые числа обязательно должны присутствовать в кубической формуле, когда уравнение имеет три действительных разных корня Пьера Лорана Ванцеля в 1843 году, Винченцо Молламе в 1890 году, Отто Гёльдера в 1891 году и Адольфа Кнезера в 1892 году. неполное доказательство 1799 г.
23. Декарт, Рене (1954) [1637], La Géométrie | Геометрия Рене Декарта с факсимиле первого издания, Dover Publications, ISBN  978-0-486-60068-0, получено 20 апреля 2011
24. Эйлер, Леонард (1748). Введение в Analysin Infinitorum [Введение в анализ бесконечного] (на латыни). т. 1. Люцерн, Швейцария: Marc Michel Bosquet & Co. p. 104.
25. Вессель, Каспар (1799). "Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning" [Об аналитическом представлении направления, усилия, приложенные, в частности, для определения плоских и сферических многоугольников]. Nye Samling af Det Kongelige Danske Videnskabernes Selskabs Skrifter [Новое собрание сочинений Королевского датского научного общества] (на датском). 5: 469–518.
26. Уоллис, Джон (1685). Трактат по алгебре, как исторической, так и практической…. Лондон, Англия: напечатано Джоном Плейфордом для Ричарда Дэвиса. С. 264–273.
27. Арган (1806 г.). Essai sur une manière de représenter les Quantités imaginaires dans les constructions géométriques [Эссе о способе представления сложных величин геометрическими конструкциями] (На французском). Париж, Франция: Мадам Вдова Блан.
28. Гаусс, Карл Фридрих (1799) "Demonstratio nova Theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse". [Новое доказательство теоремы о том, что любая рациональная интегральная алгебраическая функция одной переменной может быть разложена на действительные множители первой или второй степени.] Кандидат наук. защитил диссертацию в Университете Хельмштедта (Германия). (на латыни)
29. Гаусс, К.Ф. (1831 г.). "Anzeige von Theoria резидуум biquadraticorum, commentatio secunda" [Замечание по теории биквадратичных вычетов, второй трактат]. Göttingische gelehrte Anzeigen: 638.
30. Эвальд, Уильям Б. (1996). От Канта до Гильберта: Справочник по основам математики. 1. Издательство Оксфордского университета. п. 313. ISBN  9780198505358. Получено 18 марта 2020.
31. Адриан Квентин Буэ (1745–1845): MacTutor
32. Буэ (1806). "Mémoire sur les Quantités Imminaires" [Воспоминания о мнимых величинах]. Философские труды Лондонского королевского общества (На французском). 96: 23–88. Дои:10.1098 / рстл.1806.0003. S2CID  110394048.
33. Мурей, К.В. (1861). La vraies théore des Quantités négatives et des Quantités pretendues imaginaires [Истинная теория отрицательных величин и предполагаемых мнимых величин] (На французском). Париж, Франция: Малле-Башелье. 1861 г. Переиздание оригинала 1828 г.
34. Видеть:
    • Уоррен, Джон (1828). Трактат о геометрическом представлении квадратных корней отрицательных величин. Кембридж, Англия: Издательство Кембриджского университета.
    • Уоррен, Джон (1829). «Рассмотрение возражений против геометрического представления квадратных корней из отрицательных величин». Философские труды Лондонского королевского общества. 119: 241–254. Дои:10.1098 / рстл.1829.0022. S2CID  186211638.
    • Уоррен, Джон (1829). «О геометрическом представлении степеней величин, в индексы которых входят квадратные корни из отрицательных чисел». Философские труды Лондонского королевского общества. 119: 339–359. Дои:10.1098 / рстл.1829.0031. S2CID  125699726.
35. Français, J.F. (1813). "Новые принципы геометрической позиции и геометрическая интерпретация воображаемых символов" [Новые принципы геометрии положения и геометрическая интерпретация сложных [числовых] символов]. Анналы чистой математики и аппликации (На французском). 4: 61–71.
36. Капаррини, Сандро (2000), «Об общем происхождении некоторых работ по геометрической интерпретации комплексных чисел», в Ким Уильямс (ред.), Две культуры, Биркхойзер, стр. 139, ISBN  978-3-7643-7186-9 Отрывок страницы 139 В архиве 2 декабря 2016 г. Wayback Machine
37. Харди, G.H .; Райт, Э.М. (2000) [1938], Введение в теорию чисел, ОУП Оксфорд, п. 189 (издание четвертое), ISBN  978-0-19-921986-5
38. Арган (1814 г.). "Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la демонстрация d'un theorème d'analise" [Размышления о новой теории комплексных чисел с последующим приложением к доказательству теоремы анализа]. Анналы чистой математики и аппликации (На французском). 5: 197–209. На стр. 204, Арган определяет модуль комплексного числа, но не называет его: "Dans ce qui suit, les acns, indifféremment placés, seront Employers pour indiquer la grandeur absolue des Quantités qu'ilsffectent; ainsi, si ${displaystyle a=m+n{sqrt {-1}}}$, ${displaystyle m}$ et ${displaystyle n}$ étant réels, на Devra entender que ${displaystyle a_{'}}$ ОУ ${displaystyle a'={sqrt {m^{2}+n^{2}}}}$." (В дальнейшем акцентные знаки, где бы они ни находились, будут использоваться для обозначения абсолютного размера величин, которым они присвоены; таким образом, если ${displaystyle a=m+n{sqrt {-1}}}$, ${displaystyle m}$ и ${displaystyle n}$ будучи реальным, нужно понимать, что ${displaystyle a_{'}}$ или же ${displaystyle a'={sqrt {m^{2}+n^{2}}}}$.)
    На стр. 208, Арганд определяет и называет модуль и фактор направления комплексного числа: " ... ${displaystyle a={sqrt {m^{2}+n^{2}}}}$ Pourrait être appelé le модуль де ${displaystyle a+b{sqrt {-1}}}$, et représenterait la абсолютное величие де ла Линь ${displaystyle a+b{sqrt {-1}}}$, tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction ". ( ... ${displaystyle a={sqrt {m^{2}+n^{2}}}}$ можно было бы назвать модуль из ${displaystyle a+b{sqrt {-1}}}$ и будет представлять абсолютный размер линии ${displaystyle a+b{sqrt {-1}}}$ [Примечание: Арганд представлял комплексные числа как векторы.], Тогда как другой фактор [а именно, ${displaystyle { frac {a}{sqrt {a^{2}+b^{2}}}}+{ frac {b}{sqrt {a^{2}+b^{2}}}}{sqrt {-1}}}$], модуль которого равен единице [1], будет представлять его направление.)
    Смотрите также:
    • Джефф Миллер (1999) Самые ранние известные варианты использования некоторых слов математики (M), Интернет-архив Wayback Machine
39. Коши, Огюстен Луи (1821). Cours d'analyse de l'École royale polytechnique (На французском). т. 1. Париж, Франция: L'Imprimerie Royale. п. 183.
40. Гаусс, К.Ф. (1831 г.). "Theoria резидуум biquadraticorum. Комментарий secunda" [Теория биквадратных вычетов. Второй мемуар. Комментарии Societatis Regiae Scientiarum Gottingensis Recentiores (на латыни). 7: 89–148. С п. 96: "Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita Теорема приблизительно остатка biquadratica tunc tantum в summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad количественный воображаемые extensionitur, ita ut absque Restrictione ipsius obiectum constituant numeri formae а + биденотантибус я, pro more количественное воображение √ -1, atque а, б неопределенный omnes numeros, reales integros inter -${displaystyle infty }$ et +${displaystyle infty }$." (Конечно, как высшая арифметика до сих пор исследовалась в задачах только для действительных целых чисел, так и теоремы, касающиеся биквадратичных вычетов, сияют величайшей простотой и подлинной красотой, когда область арифметики расширяется до воображаемый количества, так что без ограничений числа вида а + би — я обозначая условно мнимую величину √ -1, а переменные а, б [обозначает] все действительные целые числа между -${displaystyle infty }$ и +${displaystyle infty }$ - составляют объект.)
41. Гаусс, К.Ф. (1831 г.). "Theoria резидуум biquadraticorum. Комментарий secunda" [Теория биквадратных вычетов. Второй мемуар. Комментарии Societatis Regiae Scientiarum Gottingensis Recentiores (на латыни). 7: 89–148. С п. 96: "Tales numeros vkabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam разновидностей sub his contineri censeantur". (Мы будем называть такие числа [а именно числа вида а + би ] «комплексные целые числа», так что действительные [числа] рассматриваются не как противоположность комплексных [чисел], а [как] тип [числа, который], так сказать, содержится в них.)
42. Гаусс, К.Ф. (1831 г.). "Theoria резидуум biquadraticorum. Комментарий secunda" [Теория биквадратных вычетов. Второй мемуар. Комментарии Societatis Regiae Scientiarum Gottingensis Recentiores (на латыни). 7: 89–148. С п. 98: "Productum numeri complexi per numerum ipsi conunctum utriusque нормам вокамус. Pro norma itaque numeri realis, ipsius quadratum habendum est. " (Мы называем «нормой» произведение комплексного числа [например, а + ib ] со своим сопряженным [а - иб ]. Следовательно, квадрат действительного числа следует рассматривать как его норму.)
43. Ганкель, Герман (1867). Vorlesungen über die complexen Zahlen und ihre Functionen [Лекции о комплексных числах и их функциях] (на немецком). т. 1. Лейпциг, [Германия]: Леопольд Восс. п. 71. С п. 71: "Wir werden den Factor (cos φ + i sin φ) haüfig den Richtungscoefficienten nennen. " (Мы часто будем называть множитель (cos φ + i sin φ) «коэффициентом направления».)
44. О прежних обозначениях см. (Апостол 1981 г. ), страницы 15–16.
45. Абрамовиц, Милтон; Стегун, Ирен А. (1964), Справочник математических функций с формулами, графиками и математическими таблицами, Courier Dover Publications, стр. 17, ISBN  978-0-486-61272-0, в архиве из оригинала 23 апреля 2016 г., получено 16 февраля 2016, Раздел 3.7.26, с. 17 В архиве 10 сентября 2009 г. Wayback Machine
46. Кук, Роджер (2008), Классическая алгебра: ее природа, происхождение и использование, Джон Уайли и сыновья, стр. 59, ISBN  978-0-470-25952-8, в архиве из оригинала 24 апреля 2016 г., получено 16 февраля 2016, Извлечение: стр. 59 В архиве 23 апреля 2016 г. Wayback Machine
47. Видеть (Альфорс 1979 ) ошибка harv: несколько целей (2 ×): CITEREFAhlfors1979 (помощь), стр. 3.
48. Видеть (Апостол 1981 г. ), страницы 15–16.
49. Видеть (Апостол 1981 г. ), стр.25.
50. Бурбаки, Николас. «VIII.1». Общая топология. Springer-Verlag.
51. Маркер, Дэвид (1996), «Введение в модельную теорию полей», в маркере, D .; Messmer, M .; Пиллэй, А. (ред.), Модельная теория полей, Конспект лекций по логике, 5, Берлин: Springer-Verlag, стр. 1–37, ISBN  978-3-540-60741-0, МИСТЕР  1477154
52. Бурбаки, Николас. «VIII.4». Общая топология. Springer-Verlag.
53. Корри, Лео (2015). Краткая история чисел. Издательство Оксфордского университета. С. 215–16.
54. Лестер, Дж. (1994), "Треугольники I: Формы", Aequationes Mathematicae, 52: 30–54, Дои:10.1007 / BF01818325, S2CID  121095307
55. Кальман, Дэн (2008a), «Элементарное доказательство теоремы Мардена», Американский математический ежемесячный журнал, 115 (4): 330–38, Дои:10.1080/00029890.2008.11920532, ISSN  0002-9890, S2CID  13222698, в архиве из оригинала 8 марта 2012 г., получено 1 января 2012
56. Калман, Дэн (2008b), «Самая чудесная теорема в математике», Журнал онлайн-математики и ее приложений, в архиве из оригинала 8 февраля 2012 г., получено 1 января 2012
57. Grant, I.S .; Филлипс, W.R. (2008), Электромагнетизм (2-е изд.), Manchester Physics Series, ISBN  978-0-471-92712-9
58. Кевин МакКриммон (2004) Вкус иорданских алгебр, стр 64, Universitext, Springer ISBN  0-387-95447-3 МИСТЕР2014924

Процитированные работы

• Альфорс, Ларс (1979), Комплексный анализ (3-е изд.), McGraw-Hill, ISBN  978-0-07-000657-7
• Апостол, Том (1981). Математический анализ. Эддисон-Уэсли.
• Соломенцев, Э. (2001) [1994], "Комплексное число", Энциклопедия математики, EMS Press

дальнейшее чтение

• Пенроуз, Роджер (2005), Дорога к реальности: полное руководство по законам Вселенной, Альфред А. Кнопф, ISBN  978-0-679-45443-4
• Дербишир, Джон (2006), Неизвестное количество: реальная и мнимая история алгебры, Джозеф Генри Пресс, ISBN  978-0-309-09657-7
• Нидхэм, Тристан (1997), Визуальный комплексный анализ, Кларендон Пресс, ISBN  978-0-19-853447-1

Математическая

• Альфорс, Ларс (1979), Комплексный анализ (3-е изд.), McGraw-Hill, ISBN  978-0-07-000657-7
• Конвей, Джон Б. (1986), Функции одной комплексной переменной I, Спрингер, ISBN  978-0-387-90328-6
• Джоши, Капил Д. (1989), Основы дискретной математики, Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-470-21152-6
• Педое, Дэн (1988), Геометрия: комплексный курс, Дувр, ISBN  978-0-486-65812-4
• Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, BP (2007), «Раздел 5.5 Комплексная арифметика», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN  978-0-521-88068-8
• Соломенцев, Э. (2001) [1994], "Комплексное число", Энциклопедия математики, EMS Press

Исторический

• Бурбаки, Николас (1998), "Основы математики § логика: теория множеств", Элементы истории математики, Springer
• Бертон, Дэвид М. (1995), История математики (3-е изд.), Нью-Йорк: Макгроу-Хилл, ISBN  978-0-07-009465-9
• Кац, Виктор Дж. (2004), История математики, краткая версия, Эддисон-Уэсли, ISBN  978-0-321-16193-2
• Нахин, Пол Дж. (1998), Воображаемая сказка: История ${displaystyle scriptstyle {sqrt {-1}}}$, Издательство Принстонского университета, ISBN  978-0-691-02795-1

  Мягкое введение в историю комплексных чисел и начало комплексного анализа.

• Ebbinghaus, H.D .; Hermes, H .; Hirzebruch, F .; Koecher, M .; Mainzer, K .; Neukirch, J .; Prestel, A .; Реммерт, Р. (1991), Числа (изд. в твердом переплете), Springer, ISBN  978-0-387-97497-2

  Продвинутый взгляд на историческое развитие концепции числа.